1. L is a regular Language if and only If the set of __________ classes of IL is finite.
a) Equivalence
b) Reflexive
c) Myhill
d) Nerode
Answer: a
Explanation: According to Myhill Nerode theorem, the corollary proves the given statement correct for equivalence classes.
2. A language can be generated from simple primitive language in a simple way if and only if
a) It is recognized by a device of infinite states
b) It takes no auxiliary memory
c) Both are correct
d) Both are wrong
Answer: b
Explanation: A language is regular if and only if it can be accepted by a finite automaton. Secondly, It supports no concept of auxiliary memory as it loses the data as soon as the device is shut down.
3. Which of the following does not represents the given language?
Language: {0,01}
a) 0+01
b) {0} U {01}
c) {0} U {0}{1}
d) {0} ^ {01}
Answer: d
Explanation: The given option represents {0, 01} in different forms using set operations and Regular Expressions. The operator like ^, v, etc. are logical operation and they form invalid regular expressions when used.
4. According to the given language, which among the following expressions does it corresponds to?
Language L={xϵ{0,1}|x is of length 4 or less}
a) (0+1+0+1+0+1+0+1)4
b) (0+1)4
c) (01)4
d) (0+1+ε)4
Answer: d
Explanation: The extended notation would be (0+1)4 but however, we may allow some or all the factors to be ε. Thus ε needs to be included in the given regular expression.
5. Which among the following looks similar to the given expression?
((0+1). (0+1)) *
a) {xϵ {0,1} *|x is all binary number with even length}
b) {xϵ {0,1} |x is all binary number with even length}
c) {xϵ {0,1} *|x is all binary number with odd length}
d) {xϵ {0,1} |x is all binary number with odd length}
Answer: a
Explanation: The given regular expression corresponds to a language of binary strings which is of even length including a length of 0.
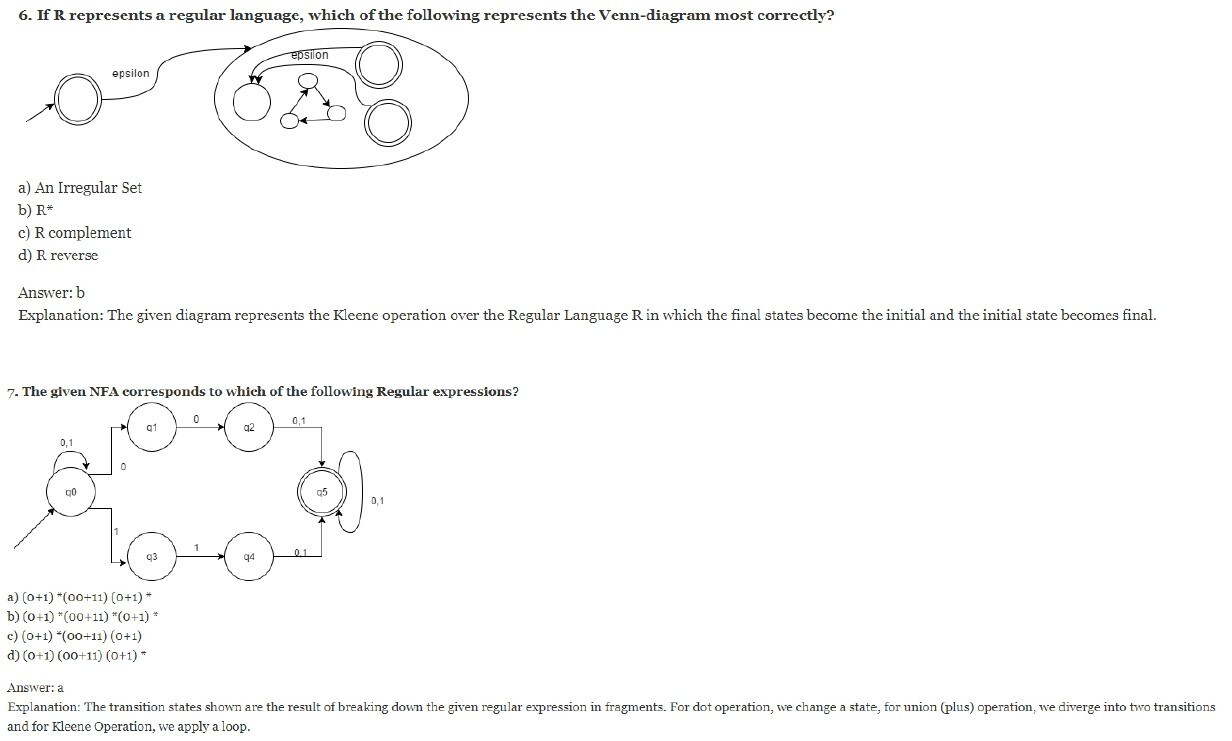
8. Concatenation Operation refers to which of the following set operations:
a) Union
b) Dot
c) Kleene
d) Two of the options are correct
Answer: b
Explanation: Two operands are said to be performing Concatenation operation AB = A•B = {xy: x ∈ A & y ∈ B}.
9. Concatenation of R with Ф outputs:
a) R
b) Ф
c) R.Ф
d) None of the mentioned
Answer: b
Explanation: By distributive property (Regular expression identities), we can prove the given identity to be Ф.
10. RR* can be expressed in which of the forms:
a) R+
b) R-
c) R+ U R-
d) R
Answer: a
Explanation: RR*=R+ as R+ means the occurrence to be at least once.
11. What kind of expressions do we used for pattern matching?
a) Regular Expression
b) Rational Expression
c) Regular & Rational Expression
d) None of the mentioned
Answer: c
Explanation: In automata theory, Regular Expression(sometimes also called the Rational Expression ) is a sequence or set of characters that define a search pattern, mainly for the use in pattern matching with strings or string matching.
12. Which of the following do Regexps do not find their use in?
a) search engines
b) word processors
c) sed
d) none of the mentioned
Answer: d
Explanation: Regexp processors are found in several search engines, seach and replace mechanisms, and text processing utilities.
13. Which of the following languages have built in regexps support?
a) Perl
b) Java
c) Python
d) C++
Answer: a
Explanation: Many languages come with built in support of regexps like Perl, Javascript, Ruby etc. While some provide support using standard libraries like .NET, Java, Python, C++, C and POSIX.
14. The following is/are an approach to process a regexp:
a) Contruction of NFA and subsequently, a DFA.
b) Thompson’s Contruction Algorithm
c) Both (a) and (b)
d) None of the mentioned
Answer: c
Explanation: A regexp processor translates the syntax into internal representation which can be executed and matched with a string and that internal representation can have several approaches like the ones mentioned.
15. Are the given two patterns equivalent?
(1) gray|grey
(2) gr(a|e)y
a) yes
b) no
Answer: a
Explanation: Paranthesis can be used to define the scope and precedence of operators. Thus, both the expression represents the same pattern.
16. Which of the following are not quantifiers?
a) Kleene plus +
b) Kleene star *
c) Question mark ?
d) None of the mentioned
Answer: d
Explanation: A quantifier after a token specifies how often the preceding element is allowed to occur. ?, *, +, {n}, {min, }, {min, max} are few quantifiers we use in regexps implementations.
17. Which of the following cannot be used to decide whether and how a given regexp matches a string:
a) NFA to DFA
b) Lazy DFA algorithm
c) Backtracking
d) None of the mentioned
Answer: d
Explanation: There are at least three algorithms which decides for us, whether and how a regexp matches a string which included the transformation of Non deterministic automaton to deterministic finite automaton, The lazy DFA algorithm where one simulates the NFA directly, building each DFA on demand and then discarding it at the next step and the process of backtracking whose running time is exponential.
18. What does the following segment of code output?
$string1 = "Hello World\n";
if ($string1 =~ m/(H..).(l..)/) {
print "We matched '$1' and '$2'.\n";
}a) We matched ‘Hel’ and ‘ld’
b) We matched ‘Hel’ and ‘lld’
c) We matched ‘Hel’ and ‘lo ‘
d) None of the mentioned
Answer: c
Explanation: () groups a series of pattern element to a single element.
When we use pattern in parenthesis, we can use any of ‘$1’, ‘$2’ later to refer to the previously matched pattern.
9. Given segment of code:
$string1 = "Hello\nWorld\n";
if ($string1 =~ m/d\n\z/) {
print "$string1 is a string ";
print "that ends with 'd\\n'.\n";
}What does the symbol /z does?
a) changes line
b) matches the beginning of a string
c) matches the end of a string
d) none of the mentioned
Answer: c
Explanation: It matches the end of a string and not an internal line.The given segment of code outputs:
Hello
World
is a string that ends with ‘d\n’
20. Conversion of a regular expression into its corresponding NFA :
a) Thompson’s Construction Algorithm
b) Powerset Construction
c) Kleene’s algorithm
d) None of the mentioned
Answer: a
Explanation: Thompson construction algorithm is an algorithm in automata theory used to convert a given regular expression into NFA. Similarly, Kleene algorithm is used to convert a finite automaton to a regular expression.
21. A regular language over an alphabet a is one that can be obtained from
a) union
b) concatenation
c) kleene
d) All of the mentioned
Answer: d
Explanation: None.
22. Regular expression {0,1} is equivalent to
a) 0 U 1
b) 0 / 1
c) 0 + 1
d) All of the mentioned
Explanation: All are equivalent to union operation.
23. Precedence of regular expression in decreasing order is
a) * , . , +
b) . , * , +
c) . , + , *
d) + , a , *
Answer: a
Explanation: None.
24. Regular expression Φ* is equivalent to
a) ϵ
b) Φ
c) 0
d) 1
Answer: a
Explanation: None.
25. a? is equivalent to
a) a
b) a+Φ
c) a+ϵ
d) wrong expression
Answer: c
Explanation: Zero or one time repetition of previous character .
26. ϵL is equivalent to
a) ϵ
b) Φ
c) L
d) Lϵ
Answer: c,d
Explanation: None.
27. (a+b)* is equivalent to
a) b*a*
b) (a*b*)*
c) a*b*
d) none of the mentioned
Answer: b
Explanation: None.
28. ΦL is equivalent to
a) LΦ
b) Φ
c) L
d) ϵ
Explanation: None.
29. Which of the following pair of regular expression are not equivalent?
a) 1(01)* and (10)*1
b) x(xx)* and (xx)*x
c) (ab)* and a*b*
d) x+ and x*x+
Answer: c
Explanation: (ab)*=(a*b*)*.
30. Consider following regular expression
i) (a/b)* ii) (a*/b*)* iii) ((ϵ/a)b*)*
Which of the following statements is correct
a) i,ii are equal and ii,iii are not
b) i,ii are equal and i,iii are not
c) ii,iii are equal and i,ii are not
d) all are equal
Answer: d
Explanation: All are equivalent to (a+b)*.
31. If L1, L2 are regular and op(L1, L2) is also regular, then L1 and L2 are said to be ____________ under an operation op.
a) open
b) closed
c) decidable
d) none of the mentioned
Answer: b
Explanation: If two regular languages are closed under an operation op, then the resultant of the languages over an operation op will also be regular.
32. Suppose a regular language L is closed under the operation halving, then the result would be:
a) 1/4 L will be regular
b) 1/2 L will be regular
c) 1/8 L will be regular
d) Al of the mentioned
Answer: d
Explanation: At first stage 1/2 L will be regular and subsequently, all the options will be regular.
33. If L1′ and L2′ are regular languages, then L1.L2 will be
a) regular
b) non regular
c) may be regular
d) none of the mentioned
Answer: a
Explanation: Regular language is closed under complement operation. Thus, if L1′ and L2′ are regular so are L1 and L2. And if L1 and L2 are regular so is L1.L2.
34. If L1 and L2′ are regular languages, L1 ∩ (L2′ U L1′)’ will be
a) regular
b) non regular
c) may be regular
d) none of the mentioned
Answer: a
Explanation: If L1 is regular, so is L1′ and if L1′ and L2′ are regular so is L1′ U L2′. Further, regular languages are also closed under intersection operation.
35. If A and B are regular languages, !(A’ U B’) is:
a) regular
b) non regular
c) may be regular
d) none of the mentioned
Answer: a
Explanation: If A and B are regular languages, then A Ç B is a regular language and A ∩ B is equivalent to !(A’ U B’).
36. Which among the following are the boolean operations that under which regular languages are closed?
a) Union
b) Intersection
c) Complement
d) All of the mentioned
Answer: d
Explanation: Regular languages are closed under the following operations:
a) Regular expression operations
b) Boolean operations
c) Homomorphism
d) Inverse Homomorphism
37. Suppose a language L1 has 2 states and L2 has 2 states. After using the cross product construction method, we have a machine M that accepts L1 ∩ L2. The total number of states in M:
a) 6
b) 4
c) 2
d) 8
Answer: 4
Explanation: M is defined as: (Q, S, d, q0, F)
where Q=Q1*Q2 and F=F1*F2
38. If L is a regular language, then (L’)’ U L will be :
a) L
b) L’
c) f
d) none of the mentioned
Answer: a
Explanation: (L’)’ is equivalent to L and L U L is subsequently equivalent to L.
39. If L is a regular language, then (((L’)r)’)* is:
a) regular
b) non regular
c) may be regular
d) none of the mentioned
Answer: a
Explanation: If L is regular so is its complement, if L’ is regular so is its reverse, if (L’)r is regular so is its Kleene.
40. Which among the following is the closure property of a regular language?
a) Emptiness
b) Universality
c) Membership
d) None of the mentioned
Answer: d
Explanation: All the following mentioned are decidability properties of a regular language. The closure properties of a regular language include union, concatenation, intersection, Kleene, complement , reverse and many more operations.
41. Relate the following statement:
Statement: All sufficiently long words in a regular language can have a middle section of words repeated a number of times to produce a new word which also lies within the same language.
a) Turing Machine
b) Pumping Lemma
c) Arden’s theorem
d) None of the mentioned
Answer: b
Explanation: Pumping lemma defines an essential property for every regular language in automata theory. It has certain rules which decide whether a language is regular or not.
42. While applying Pumping lemma over a language, we consider a string w that belong to L and fragment it into _________ parts.
a) 2
b) 5
c) 3
d) 6
Answer: c
Explanation: We select a string w such that w=xyz and |y|>0 and other conditions. However, there exists an integer n such that |w|>=n for any wÎL.
43. If we select a string w such that w∈L, and w=xyz. Which of the following portions cannot be an empty string?
a) x
b) y
c) z
d) all of the mentioned
View Answer
Explanation: The lemma says, the portion y in xyz cannot be zero or empty i.e. |y|>0, this condition needs to be fulfilled to check the conclusion condition.
44. Let w= xyz and y refers to the middle portion and |y|>0.What do we call the process of repeating y 0 or more times before checking that they still belong to the language L or not?
a) Generating
b) Pumping
c) Producing
d) None of the mentioned
Answer: b
Explanation: The process of repeatation is called pumping and so, pumping is the process we perform before we check whether the pumped string belongs to L or not.
45. There exists a language L. We define a string w such that w∈L and w=xyz and |w| >=n for some constant integer n.What can be the maximum length of the substring xy i.e. |xy|<=?
a) n
b) |y|
c) |x|
d) none of the mentioned
Answer: a
Explanation: It is the first conditional statement of the lemma that states that |xy|<=n, i.e. the maximum length of the substring xy in w can be n only.
46. Fill in the blank in terms of p, where p is the maximum string length in L.
Statement: Finite languages trivially satisfy the pumping lemma by having n = ______
a) p*1
b) p+1
c) p-1
d) None of the mentioned
Answer: b
Explanation: Finite languages trivially satisfy the pumping lemma by having n equal to the maximum string length in l plus 1.
47. Answer in accordance to the third and last statement in pumping lemma:
For all _______ xyiz ∈L
a) i>0
b) i<0
c) i<=0
d) i>=0
Answer: d
Explanation: Suppose L is a regular language . Then there is an integer n so that for any x∈L and |x|>=n, there are strings u,v,w so that
x= uvw
|uv|<=n
|v|>0
for any m>=0, uvmw ∈L.
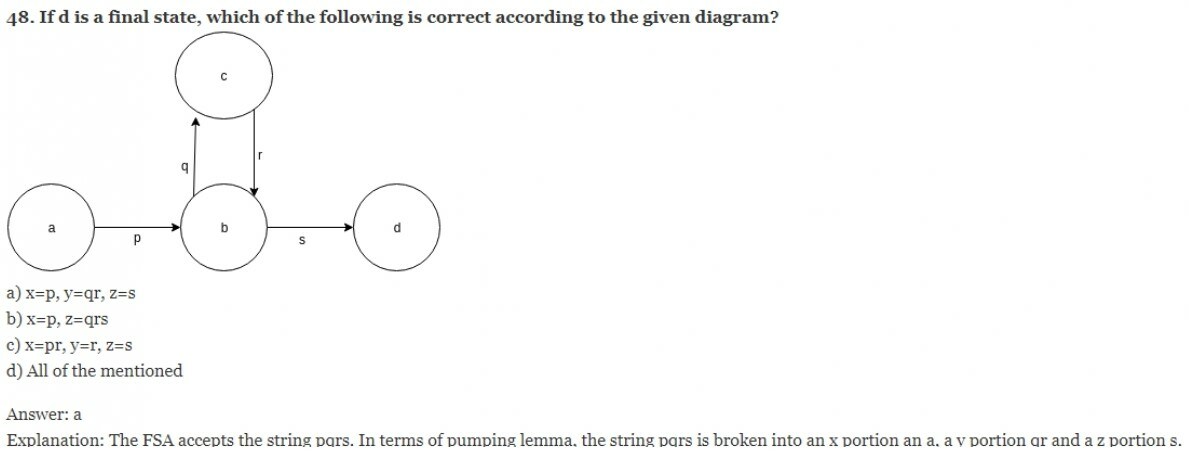
49. Let w be a string and fragmented by three variable x, y, and z as per pumping lemma. What does these variables represent?
a) string count
b) string
c) both (a) and (b)
d) none of the mentioned
Answer: a
Explanation: Given: w =xyz. Here, xyz individually represents strings or rather substrings which we compute over conditions to check the regularity of the language.
50. Which of the following one can relate to the given statement:
Statement: If n items are put into m containers, with n>m, then atleast one container must contain more than one item.
a) Pumping lemma
b) Pigeon Hole principle
c) Count principle
d) None of the mentioned
Answer: b
Explanation: Pigeon hole principle states the following example: If there exists n=10 pigeons in m=9 holes, then since 10>9, the pigeonhole principle says that at least one hole has more than one pigeon.













No comments:
Post a Comment