Definition of NP class Problem: - The set of all decision-based problems came into the division of NP Problems that can't be solved or produce an output within polynomial time but verified in the polynomial time. NP class contains P class as a subset. NP problems are hard to solve.
Note: - The term "NP" does not mean "not polynomial." Originally, the term meant "non-deterministic polynomial. It means according to the one input number of output will be produced.
Definition of P class Problem: - The set of decision-based problems come into the division of P Problems who can be solved or produced an output within polynomial time. P problems being easy to solve
Definition of Polynomial time: - If we produce an output according to the given input within a specific amount of time such as within a minute, hours. This is known as Polynomial time.
Definition of Non-Polynomial time: - If we produce an output according to the given input but there are no time constraints is known as Non-Polynomial time. But yes output will produce but time is not fixed yet.
Definition of Decision Based Problem: - A problem is called a decision problem if its output is a simple "yes" or "no" (or you may need this of this as true/false, 0/1, accept/reject.) We will phrase many optimization problems as decision problems. For example, Greedy method, D.P., given a graph G= (V, E) if there exists any Hamiltonian cycle.
Definition of NP-hard class: - Here you to satisfy the following points to come into the division of NP-hard
- If we can solve this problem in polynomial time, then we can solve all NP problems in polynomial time
- If you convert the issue into one form to another form within the polynomial time
Definition of NP-complete class: - A problem is in NP-complete, if
- It is in NP
- It is NP-hard
Pictorial representation of all NP classes which includes NP, NP-hard, and NP-complete
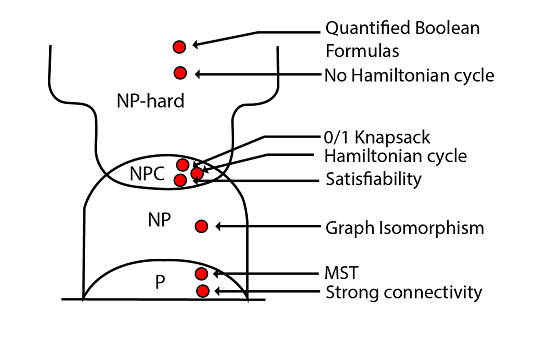
Fig: Complexity Classes
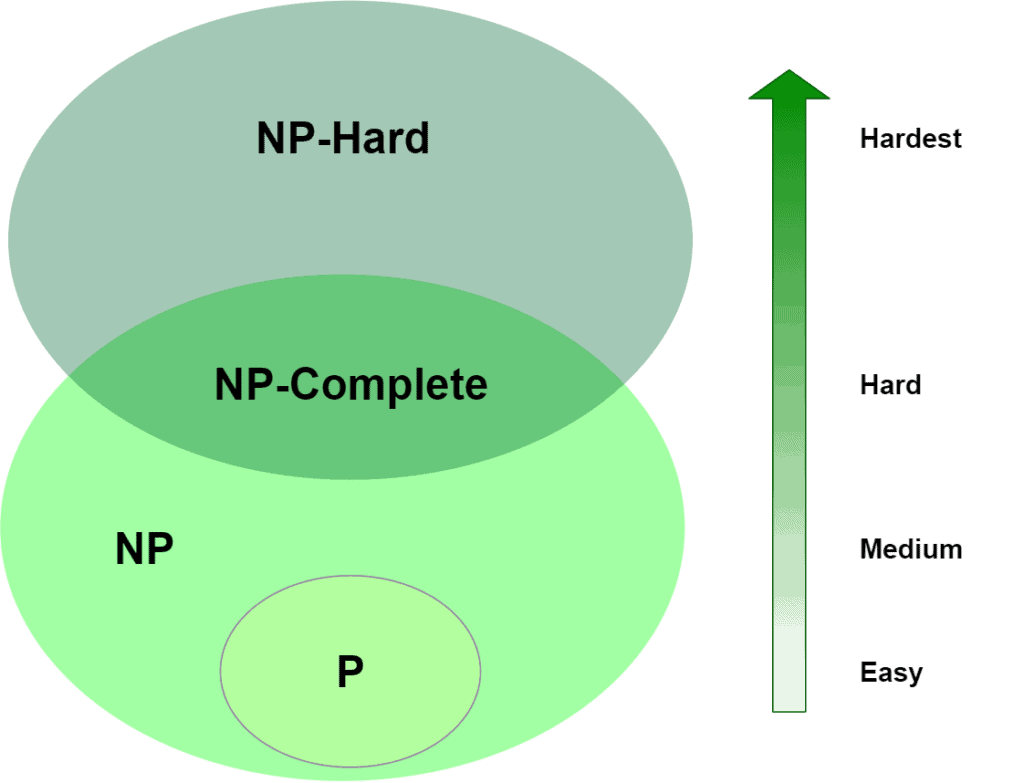
And we can visualize their relationship, too:





No comments:
Post a Comment