Finite state machine

Finite state machine

• Finite state machine is used to recognize patterns.
• Finite automata machine takes the string of symbol as input and changes its state accordingly. In the input, when a desired symbol is found then the transition occurs.
• While transition, the automata can either move to the next state or stay in the same state.
• FA has two states: accept state or reject state. When the input string is successfully processed and the automata reached its final state then it will accept.

A finite automata consists of following:

Q: finite set of states
∑: finite set of input symbol
q0: initial state
F: final state
δ: Transition function

Transition function can be define as

δ: Q x ∑ →Q  

FA is characterized into two ways:

1. DFA (finite automata)
2. NDFA (non deterministic finite automata)

DFA

DFA stands for Deterministic Finite Automata. Deterministic refers to the uniqueness of the computation. In DFA, the input character goes to one state only. DFA doesn't accept the null move that means the DFA cannot change state without any input character.

DFA has five tuples {Q, ∑, q0, F, δ}

Q: set of all states
∑: finite set of input symbol where δ: Q x ∑ →Q
q0: initial state
F: final state
δ: Transition function

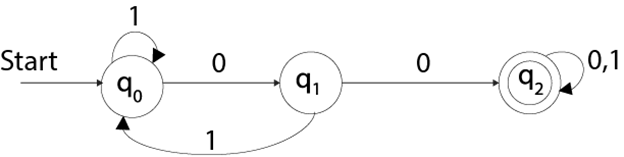
Example

See an example of deterministic finite automata:

Q = {q0, q1, q2}  
∑ = {0, 1}  
q0 = {q0}  
F = {q3}  

NDFA

NDFA refer to the Non Deterministic Finite Automata. It is used to transit the any number of states for a particular input. NDFA accepts the NULL move that means it can change state without reading the symbols.

NDFA also has five states same as DFA. But NDFA has different transition function.

Transition function of NDFA can be defined as:

δ: Q x ∑ →2^Q

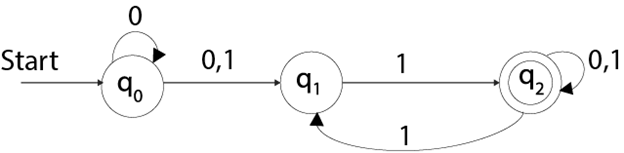
Example

See an example of non deterministic finite automata:

Q = {q0, q1, q2}  
∑ = {0, 1}  
q0 = {q0}  
F = {q3}