Hamiltonian Circuit Problems

The Hamiltonian cycle is the cycle in the graph which visits all the vertices in graph exactly once and terminates at the starting node. It may not include all the edges

• The Hamiltonian cycle problem is the problem of finding a Hamiltonian cycle in a graph if there exists any such cycle.
• The input to the problem is an undirected, connected graph. For the graph shown in Figure (a), a path A – B – E – D – C – A forms a Hamiltonian cycle. It visits all the vertices exactly once, but does not visit the edges <B, D>.

Figure (a)

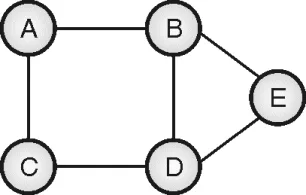
• The Hamiltonian cycle problem is also both, decision problem and an optimization problem. A decision problem is stated as, “Given a path, is it a Hamiltonian cycle of the graph?”.
• The optimization problem is stated as, “Given graph G, find the Hamiltonian cycle for the graph.”
• We can define the constraint for the Hamiltonian cycle problem as follows:
  • In any path, vertex i and (i + 1) must be adjacent.
  • 1st and (n – 1)th vertex must be adjacent (nth of cycle is the initial vertex itself).
  • Vertex i must not appear in the first (i – 1) vertices of any path.
• With the adjacency matrix representation of the graph, the adjacency of two vertices can be verified in constant time.

Algorithm for Hamiltonian Cycle Problem using Backtracking

Algorithm

Complexity Analysis

Looking at the state space graph, in worst case, total number of nodes in tree would be,

T(n) = 1 + (n – 1) + (n – 1)² + (n – 1)³ + … + (n – 1)^{n – 1}

=frac(n−1)n–1n–2

T(n) = O(nⁿ). Thus, the Hamiltonian cycle algorithm runs in exponential time.

Examples

Example: Show that given graph has a Hamiltonian cycle

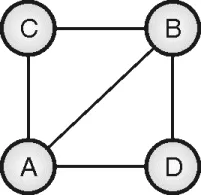
Solution:

We can start with any random vertex. Let us start with vertex A.  Neighbors of A are {B, C, D}. The inclusion of B does not lead to a complete solution. So explore it as shown in Figure (c).

Adjacent vertices to B are {C, D}. The inclusion of C does not lead to a complete solution. All adjacent vertices of C are already members of the path formed so far. So it leads to a dead end.

Backtrack and go to B and explore its next neighbor i.e. D.

The inclusion of D does not lead to a complete solution, and all adjacent vertices of D are already a member of the path formed so far. So it leads to a dead end.

Figure: (b) initial tree

Figure (c): Added node B

Figure (d): Node C added, dead-end

Figure (e): Node D added, dead-end

Backtrack and go to B. Now B does not have any more neighbors, so backtrack and go to A. Explore the next neighbor of A i.e. C. By repeating the same procedure, we get the state space trees as shown below. And path
A – C – B – D – A is detected as the Hamiltonian cycle of the input graph.

(a) initial tree	(b) Added node C	(c) Added node B	(d) Added node D, Success

Another Hamiltonian cycle with A as a start vertex is A – D – B – C – A.

Example

Example: Explain how to find Hamiltonian Cycle by using Backtracking in a given graph

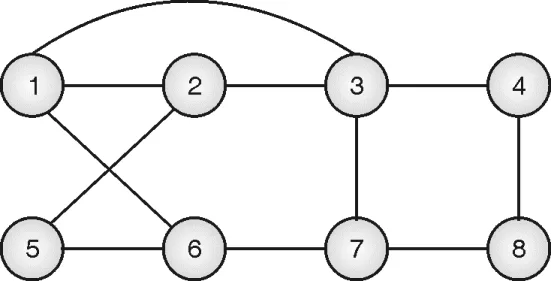
Solution:

The backtracking approach uses a state-space tree to check if there exists a Hamiltonian cycle in the graph. Figure (f) shows the simulation of the Hamiltonian cycle algorithm. For simplicity, we have not explored all possible paths, the concept is self-explanatory.

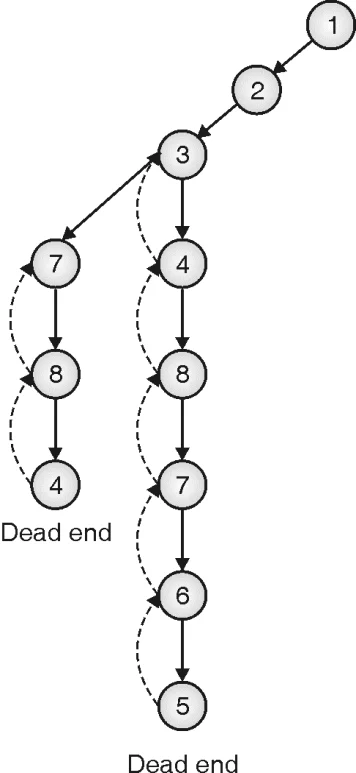
Step 1: Tour is started from vertex 1. There is no path from 5 to 1. So it’s the dead-end state.

Figure (f)

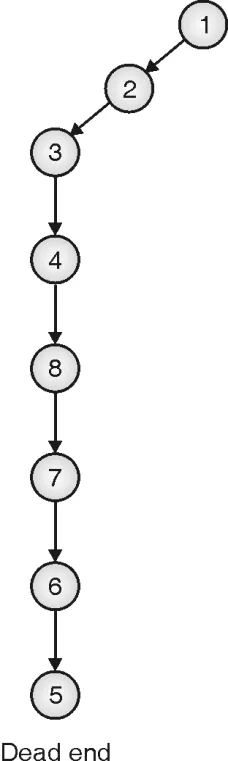
Step 2: Backtrack to the node from where the new path can be explored, that is 3 here

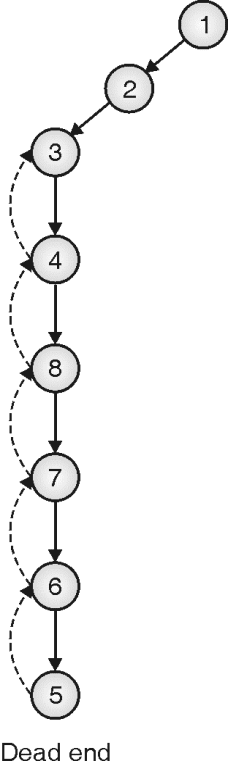
Step 3: New path also leads to a dead end so backtrack and explore all possible paths

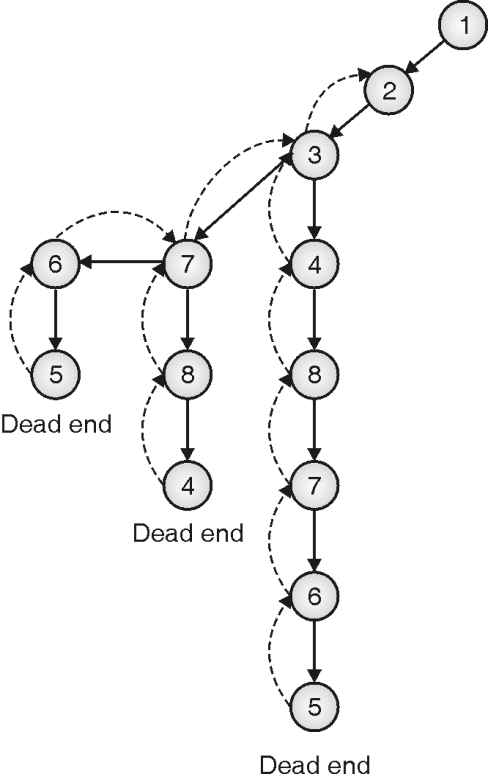
Step 4: Next path is also leading to a dead-end so keep backtracking until we get some node that can generate a new path, i.e .vertex 2 here

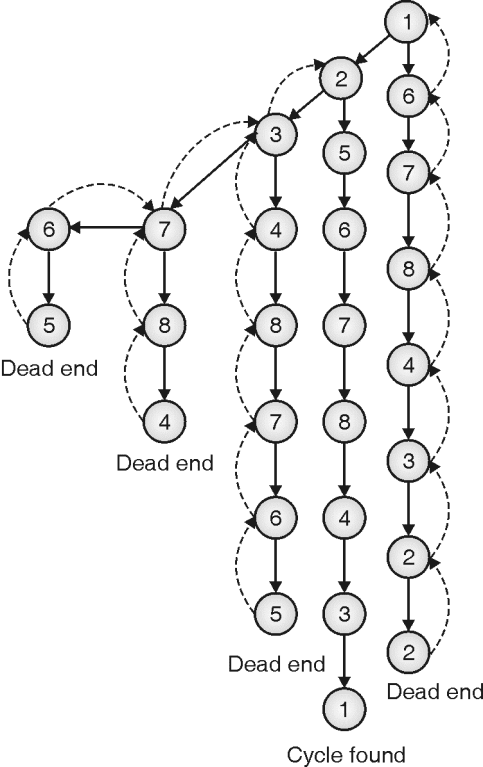
Step 5: One path leads to Hamiltonian cycle, next leads to a dead end so backtrack and explore all possible paths at each vertex

Step 6: Total two Hamiltonian cycles are detected in a given graph

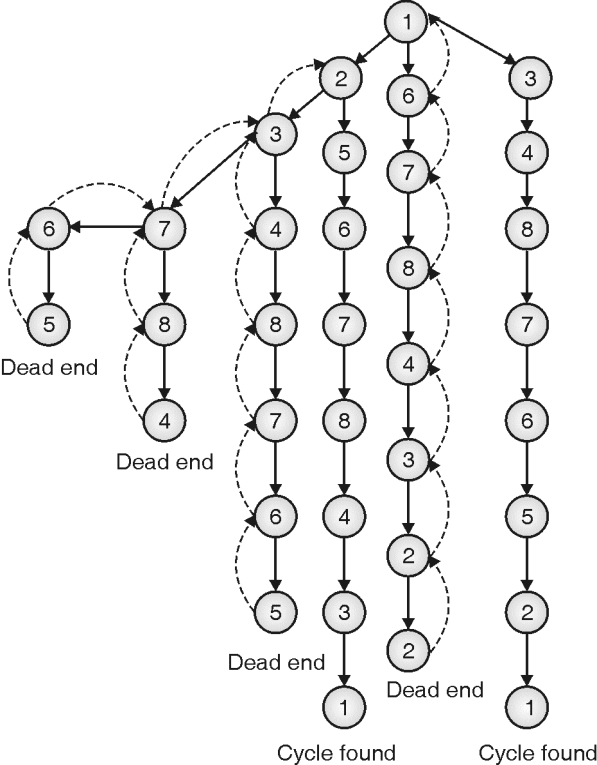
Example: Find the Hamiltonian cycle by using the backtracking approach for a given graph.

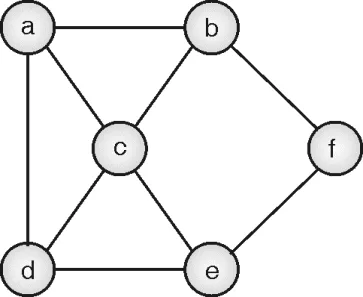
Solution:

Figure (g)

The backtracking approach uses a state-space tree to check if there exists a Hamiltonian cycle in the graph. Figure (g) shows the simulation of the Hamiltonian cycle algorithm. For simplicity, we have not explored all possible paths, the concept is self-explanatory. It is not possible to include all the paths in the graph, so few of the successful and unsuccessful paths are traced in the graph. Black nodes indicate the Hamiltonian cycle.