The (binary) heap data structure is an array object that we can view as a nearly complete binary tree. A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Macros functions:
- PARENT(i): return floor(i.2)
- LEFT(i): return 2 * i
- RIGHT(i): return 2 * i + 1
Procedure Functions:
- MAX-HEAPIFY procedure, runs in O(lg n) time, is the key to maintaining the max-heap property
- BUILD-MAX-HEAP procedure, runs in a linear time, produces a max-heap from an unordered input array
- HEAPSORT procedure, runs in O(n lg n) time, sorts an array in place
- MAX-HEAP-INSERT, HEAP-EXTRACT-MAX, HEAP-INCREASE-KEY and HEAP-MAXIMUM procedures, all runs in O(lg n) time. Those procedures are used at implementing a priority queue
The Heapsort Algorithm
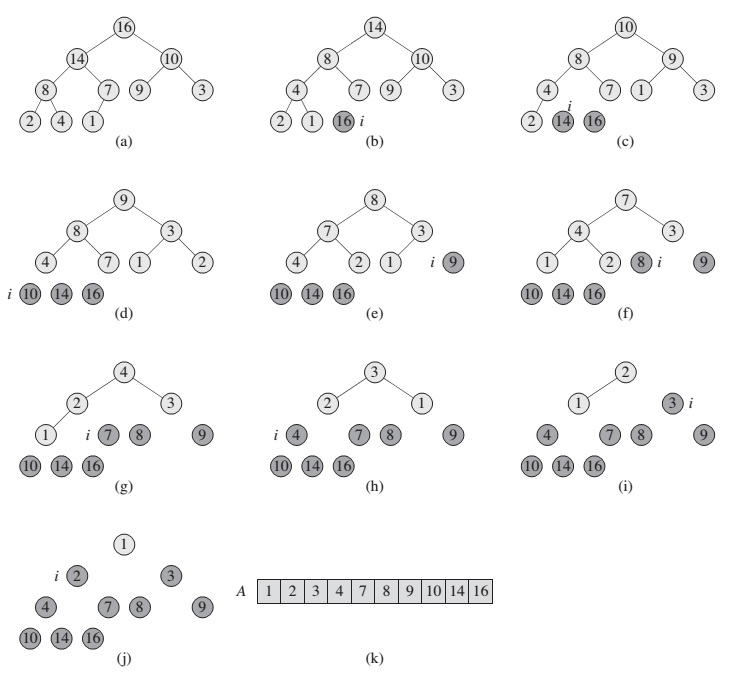
The heapsort algorithm starts with BUILD-MAX-HEAP to build a max-heap on the input array A[1 .. n], where n = A.length. Since the maximum element of the array is stored at the root A[1], we can put it into its correct final position to exchanging it with A[n].
HEAPSORT(A):
BUILD-MAX-HEAP(A)
for i = A.length downto 2
exchange A[1] with A[i]
A.heap-size = A.heap-size - 1
MAX-HEAPIFY(A, 1)Building a heap
The procedure BUILD-MAX-HEAP goes through the remaining nodes of the tree and runs MAX-HEAPIFY on each one:
BUILD-MEAX-HEAP(A):
A.heap-size = A.length
for i = floor(A.length / 2) downto 1
MAX-HEAPIFY(A, i)The time required by MAX-HEAPIFY when called on a node of height h is O(h), and so we can express the total cost of BUILD-MAX-HEAP as being bounded from above. Hence, it is possible to build a max-heap from an unordered array in a linear time.
Maintaining the heap property
MAX-HEAPIFY is the procedure which is responsible for maintaining the max-heap property. Receives an array A and index i as an input. It simply checks the LEFT(i) and RIGHT(i) child nodes of the given index i for being small. if both childs are are greater than current element then the bigger one is selected, and exchanged the positions with current node. That way the max-heap rule can be supported (max-heap rule: parrent node is bigger than childs)
MAX-HEAPIFY(A,i):
l = LEFT(i)
r = RIGHT(i)
if l <= A.heap-size and A[l] > A[i]
largest = l
else largest = i
if r <= A.heap-size and A[r] > A[largest]
largest = r
if largest != i
exchange A[i] with A[largest]
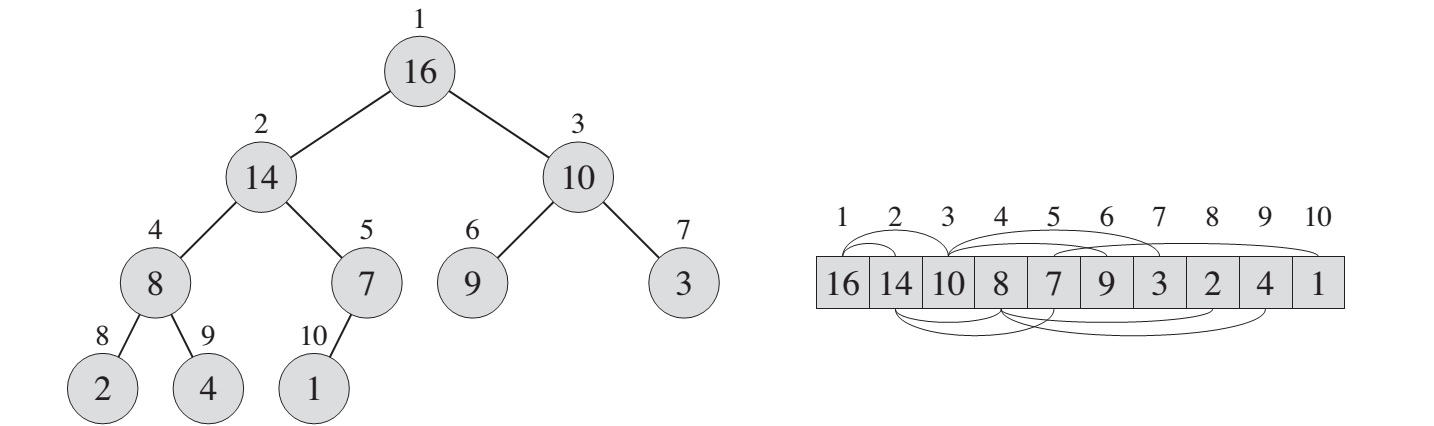
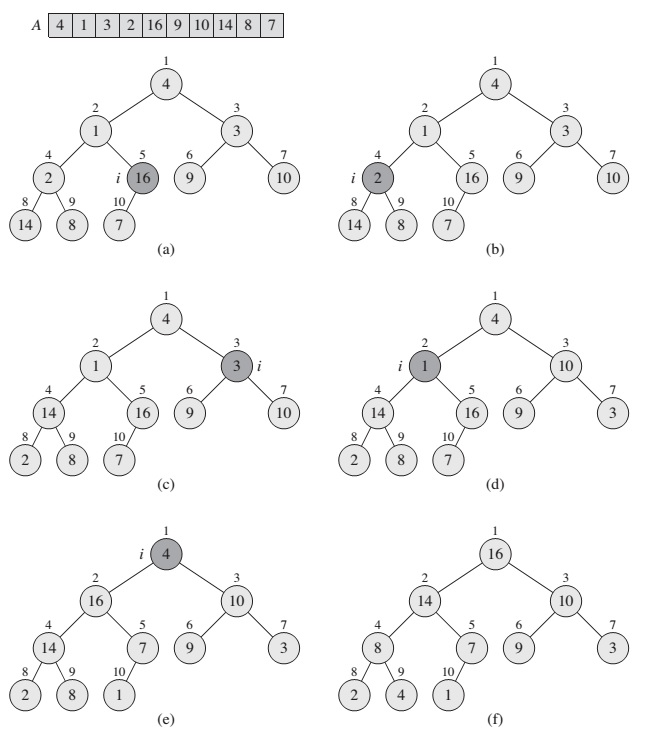
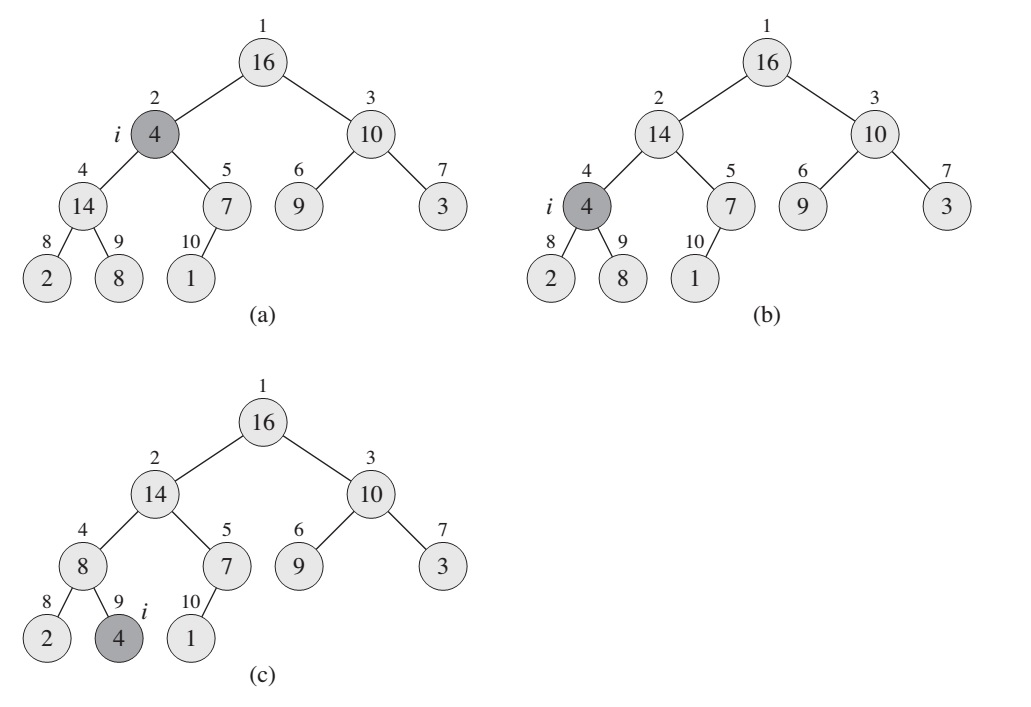
MAX-HEAPIFY(A, largest)Example:
Figure: The action of MAX-HEAPIFY(A, 2), where A.heap-size = 10
The running time of MAX-HEAPIFY on a subtree of size n rooted at a given node i is the O(1) time to fix up the relationships among elements. The children’s subtrees each have a size at most 2n/3. That is why worst case of running time of MAX-HEAPIFY by the recurrence is: T(n) <= T(2n/3) + O(1),
- The first step includes the creation of a heap by adjusting the elements of the array.
- After the creation of heap, now remove the root element of the heap repeatedly by shifting it to the end of the array, and then store the heap structure with the remaining elements.
The HEAPSORT procedure takes time O(n log n), since the call to BUILD-MAX-HEAP takes time O(n) and each of the n-1 calls to MAX-HEAPIFY takes time O(lg n)
Example:
Now let's see the working of heap sort in detail by using an example. To understand it more clearly, let's take an unsorted array and try to sort it using heap sort. It will make the explanation clearer and easier.

First, we have to construct a heap from the given array and convert it into max heap.
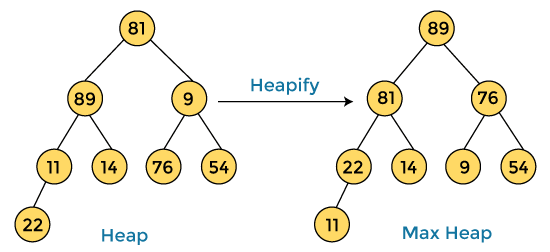
After converting the given heap into max heap, the array elements are -

Next, we have to delete the root element (89) from the max heap. To delete this node, we have to swap it with the last node, i.e. (11). After deleting the root element, we again have to heapify it to convert it into max heap.
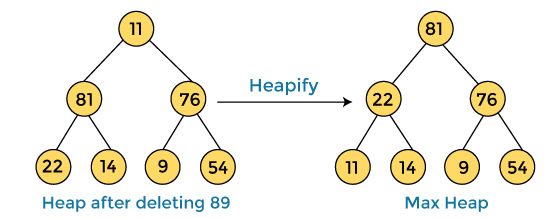
After swapping the array element 89 with 11, and converting the heap into max-heap, the elements of array are -

In the next step, again, we have to delete the root element (81) from the max heap. To delete this node, we have to swap it with the last node, i.e. (54). After deleting the root element, we again have to heapify it to convert it into max heap.
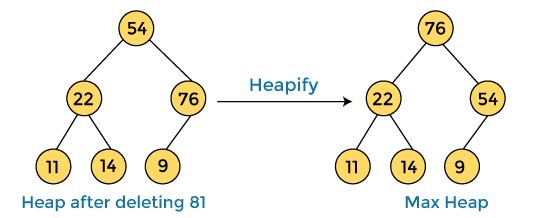
After swapping the array element 81 with 54 and converting the heap into max-heap, the elements of array are -

In the next step, we have to delete the root element (76) from the max heap again. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap.
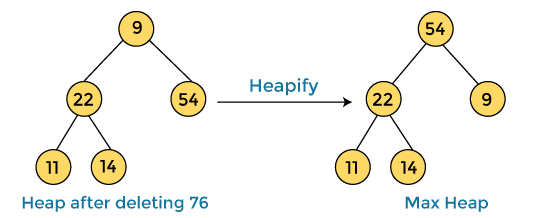
After swapping the array element 76 with 9 and converting the heap into max-heap, the elements of array are -

In the next step, again we have to delete the root element (54) from the max heap. To delete this node, we have to swap it with the last node, i.e. (14). After deleting the root element, we again have to heapify it to convert it into max heap.
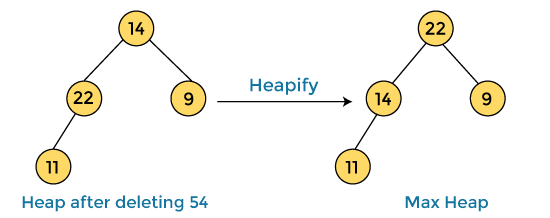
After swapping the array element 54 with 14 and converting the heap into max-heap, the elements of array are -

In the next step, again we have to delete the root element (22) from the max heap. To delete this node, we have to swap it with the last node, i.e. (11). After deleting the root element, we again have to heapify it to convert it into max heap.
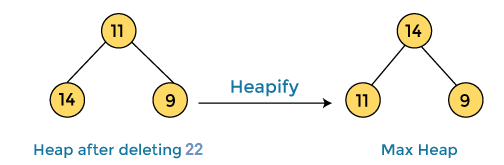
After swapping the array element 22 with 11 and converting the heap into max-heap, the elements of array are -

In the next step, again we have to delete the root element (14) from the max heap. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap.
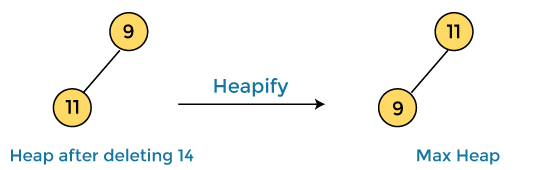
After swapping the array element 14 with 9 and converting the heap into max-heap, the elements of array are -

In the next step, again we have to delete the root element (11) from the max heap. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap.

After swapping the array element 11 with 9, the elements of array are -

Now, heap has only one element left. After deleting it, heap will be empty.

After completion of sorting, the array elements are -

Now, the array is completely sorted.





No comments:
Post a Comment