Introduction of Minimum Spanning Tree

Introduction to Minimum Spanning Tree

The minimum spanning tree algorithm is developed by referencing the field of graph theory in mathematics. Thus, to understand this algorithm, we shall first understand what a spanning tree is? 

A spanning tree of a connected undirected graph is a subgraph, i.e., a tree structure that binds all vertices with a minimum edge cost sum. If you have graph G with vertices V and edges E, then that graph can be represented as G(V, E). For this graph G(V, E), if you construct a tree structure G’(V’, E’) such that the formed tree structure follows constraints mentioned below, then that structure can be called a Spanning Tree. 

1. V’ = V   (number of Vertices in G’ must be equal to the number of vertices in G)
2. E’ = |V| - 1   (Edges of G’ must be equal to the number of vertices in graph G minus 1)

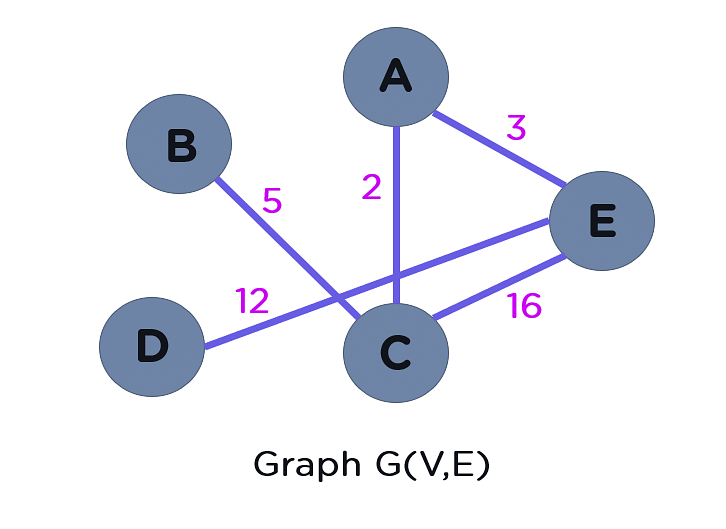
Let's create spanning trees for a given graph topology to understand this concept better.

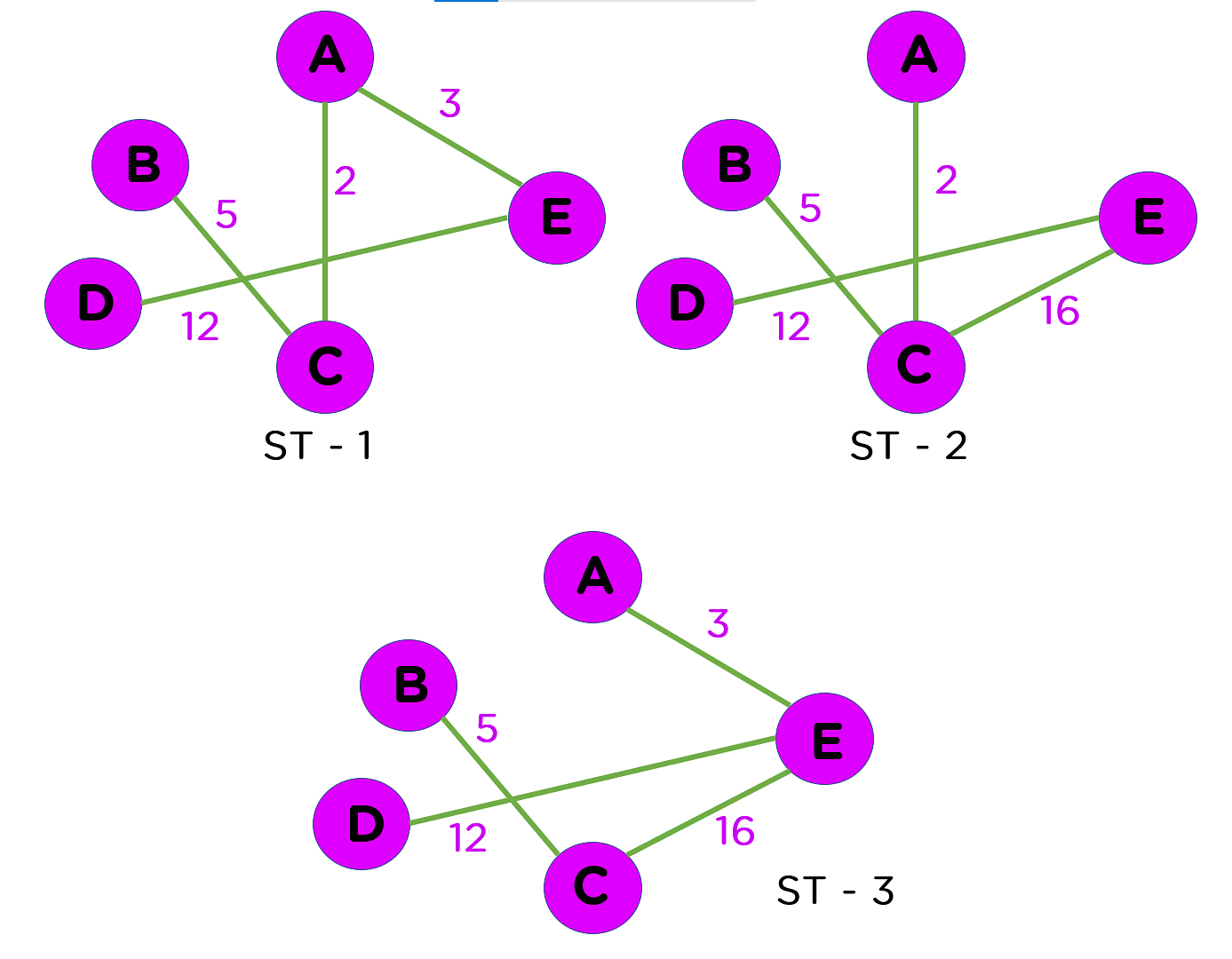
For the graph above, possible spanning tree structures are:

Now, let’s look at the sum of edge weight costs for all these spanning trees represented in the table below: 

Spanning Tree	Sum of Edge Costs
ST - 1	22
ST - 2	35
ST - 3	36

Table - 1: Sum of Edge costs

The spanning tree structure 1 has an overall edge weight cost of 22. Which is the least possible substructure cost for given graph G. Thus, ST-1 is considered the minimum spanning tree of graph G. A minimum spanning tree in a weighted graph is one that has the least weight of all the other spanning tree structures.

How to Find the Minimum Spanning Tree?

The naive method we discussed above is not an ideal approach to find out possible MST structures. In that method, we will have to generate all possible spanning trees at first and then calculate the overall sum of edge weights for each generated spanning tree. After that, we will have to determine the minima of all those spanning trees, which will cost us more time and memory. 

A better method is to locate a vital attribute of the MST, which will provide clarification if some particular edge should be included in it or not. And then, we can use that property to build up the MST gradually. Let’s find out how we can do that with the help of the greedy programming paradigm. The greedy algorithms that we can use are Prim’s Algorithm and Kruskal’s Algorithm. 

1. Prim’s Algorithm

Prim's algorithm begins with a single node and adds up adjacent nodes one by one by discovering all of the connected edges along the way. Edges with the lowest weights that don't generate cycles are chosen for inclusion in the MST structure. As a result, we can claim that Prim's algorithm finds the globally best answer by making locally optimal decisions.

2. Kruskal’s Algorithm

Kruskal's approach sorts all the edges in ascending order of edge weights and only adds nodes to the tree if the chosen edge does not form a cycle. It also selects the edge with the lowest cost first and the edge with the highest cost last. As a result, we can say that the Kruskal algorithm makes a locally optimum decision in the hopes of finding the global optimal solution. Hence, this algorithm can also be considered as a Greedy Algorithm.

Properties of Spanning Tree:

1. There may be several minimum spanning trees of the same weight having the minimum number of edges.
2. If all the edge weights of a given graph are the same, then every spanning tree of that graph is minimum.
3. If each edge has a distinct weight, then there will be only one, unique minimum spanning tree.
4. A connected graph G can have more than one spanning trees.
5. A disconnected graph can't have to span the tree, or it can't span all the vertices.
6. Spanning Tree doesn't contain cycles.
7. Spanning Tree has (n-1) edges where n is the number of vertices.

Addition of even one single edge results in the spanning tree losing its property of Acyclicity and elimination of one single edge results in its losing the property of connectivity.

Application of Minimum Spanning Tree

1. Consider n stations are to be linked using a communication network & laying of communication links between any two stations involves a cost.
   The ideal solution would be to extract a subgraph termed as minimum cost spanning tree.
2. Suppose you want to construct highways or railroads spanning several cities then we can use the concept of minimum spanning trees.
3. Designing Local Area Networks.
4. Laying pipelines connecting offshore drilling sites, refineries and consumer markets.
5. Suppose you want to apply a set of houses with
   • Electric Power
   • Water
   • Telephone lines
   • Sewage lines

To reduce cost, you can connect houses with minimum cost spanning trees.

The following are the applications of minimum spanning tree in data structures:

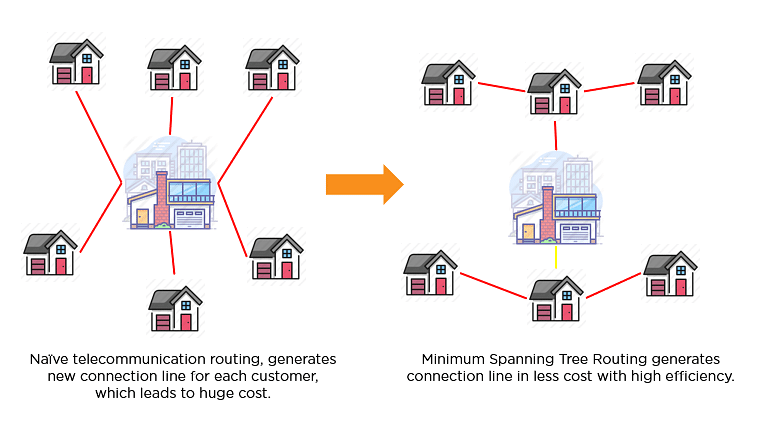
• Telecommunication Network Building: A basic naive approach will be more expensive if we develop a telecommunication network for the entire city. Using the MST approach in data structures, we can design a communication system at a much lesser cost. The distinction between Naive and MST routing is illustrated in the diagram below.

• Constructing Highways or Railroads: The Minimum Spanning Tree (MST) technique is used globally for building roadways or railroads. The MST approach determines the best route between two cities depending on all potential routes. Essentially, the algorithm treats cities as vertices and roads connecting them as edges to produce a subtree that connects two cities with less cost.