Isomorphism and Homeomorphism of graphs

Isomorphic Graphs

Consider a graph G(V, E) and G* (V*,E*) are said to be isomorphic if there exists one to one correspondence i.e. f:V→V* such that {u, v} is an edge of G if and only if {f(u), f(v)} is an edge of G*.

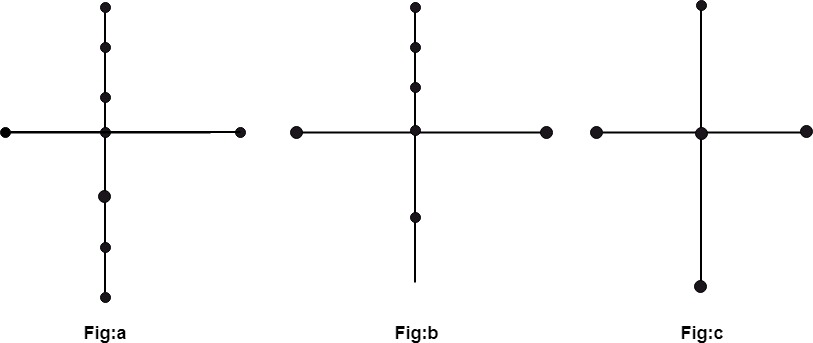
Number of vertices of graph (a) must be equal to graph (b), i.e., one to one correspondence some goes for edges.

Homeomorphic Graphs:

Two graphs G and G* are said to homeomorphic if they can be obtained from the same graph or isomorphic graphs by this method. The graphs (a) and (b) are not isomorphic, but they are homeomorphic since they can be obtained from the graph (c) by adding appropriate vertices.

Subgraph:

A subgraph of a graph G=(V, E) is a graph G'=(V',E') in which V'⊆V and E'⊆E and each edge of G' have the same end vertices in G' as in graph G.

Note: A single vertex is a subgraph.

Example: Consider the graph G shown in fig. Show the different subgraph of this graph.

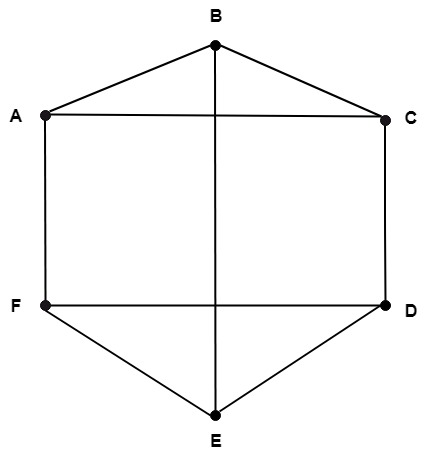
Solution: The following are all subgraphs of the above graph as shown in fig:

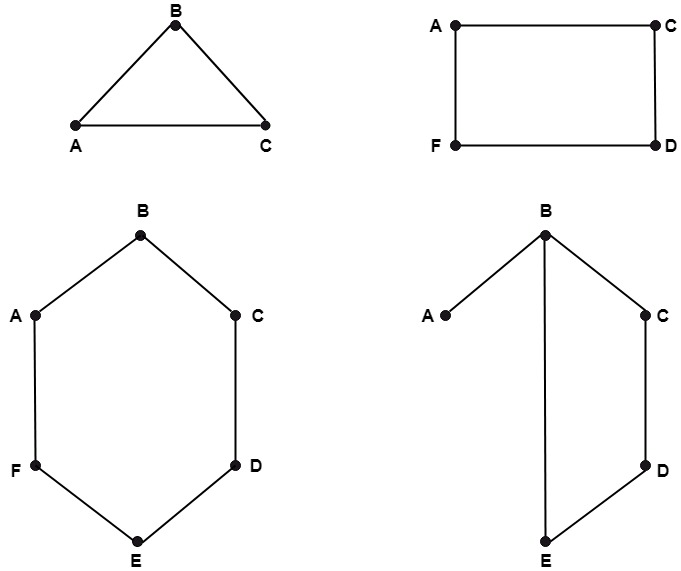
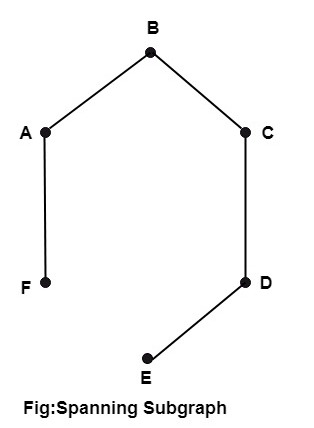
Spanning Subgraph:

A graph G₁ is called a spanning subgraph of G if G₁ contains all the vertices of G.

Example: The following fig is the spanning subgraph of the graph shown in Fig: