Prim's Algorithm

Prim's Algorithm is used to find the minimum spanning tree from a graph. Prim's algorithm finds the subset of edges that includes every vertex of the graph such that the sum of the weights of the edges can be minimized.

Prim's algorithm starts with the single node and explores all the adjacent nodes with all the connecting edges at every step. The edges with the minimal weights causing no cycles in the graph got selected.

The algorithm is given as follows.

EXAMPLE:
Use Prim’s Algorithm to find a minimal spanning tree for the graph shown below starting with the vertex A.

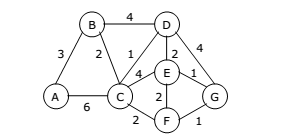
Solution:

The stepwise progress of the prim’s algorithm is as follows:

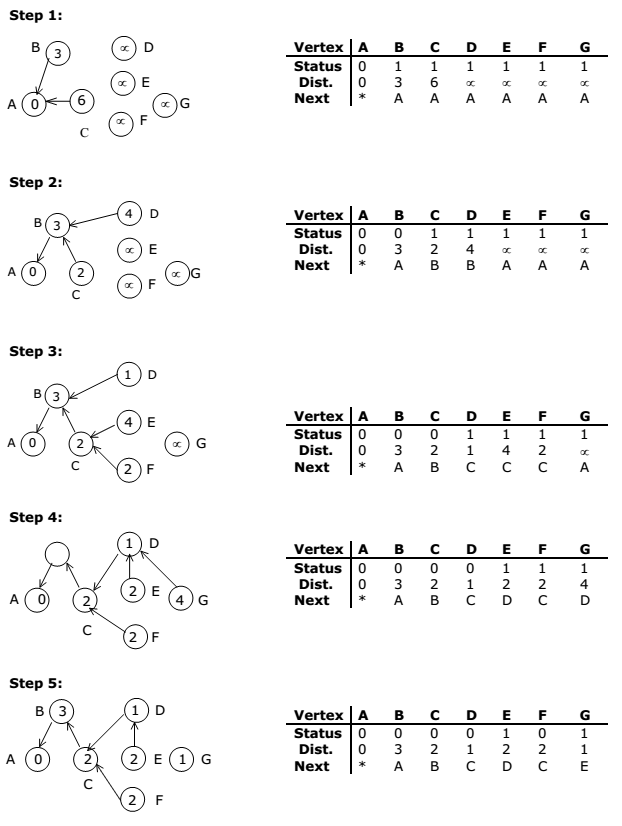
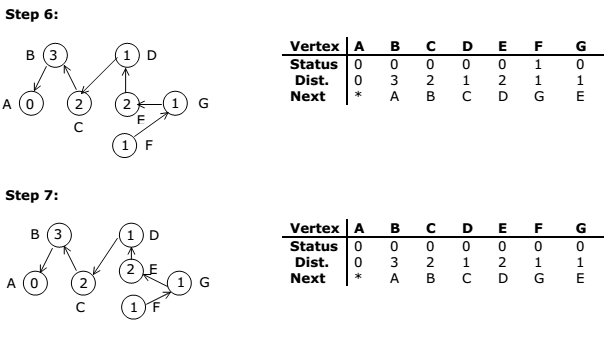
C Program:

#include <stdio.h>  
#include <limits.h>  
#define vertices 5  
  
int minimum_key(int k[], int mst[])  
{  
   int minimum  = INT_MAX, min,i;  
   
   for (i = 0; i < vertices; i++)  
     if (mst[i] == 0 && k[i] < minimum )  
         minimum  = k[i], min = i;  
   
   return min;  
}  
  
   
void prim(int g[vertices][vertices])  
{  
     int parent[vertices];   
     int k[vertices];     
     int mst[vertices];    
     int i, count,u,v;   
     for (i = 0; i < vertices; i++)  
        k[i] = INT_MAX, mst[i] = 0;  
   
     k[0] = 0;       
     parent[0] = -1;   
   
     for (count = 0; count < vertices-1; count++)  
     {  
     
        u = minimum_key(k, mst);  
      mst[u] = 1;  
   
        for (v = 0; v < vertices; v++)  
   
          if (g[u][v] && mst[v] == 0 && g[u][v] <  k[v])  
             parent[v]  = u, k[v] = g[u][v];  
     }  
   
    for (i = 1; i < vertices; i++)  
      printf("%d  %d    %d \n", parent[i], i, g[i][parent[i]]);  
}  
   
   
void main()  
{  
   int g[vertices][vertices] = {{3, 2, 1, 9, 0},  
                      {5, 1, 2, 10, 4},  
                      {0, 4, 1, 0, 9},  
                      {8, 10, 0, 2, 10},  
                      {1, 6, 8, 11, 0},  
                     };  
   
    prim(g);  
}

Output:

0  1    5 
0  2    0 
0  3    8 
1  4    6