Types of Sets

Sets can be classified into many categories. Some of which are finite, infinite, subset, universal, proper, power, singleton set, etc.

1. Finite Sets: A set is said to be finite if it contains exactly n distinct element where n is a non-negative integer. Here, n is said to be "cardinality of sets." The cardinality of sets is denoted by|A|, # A, card (A) or n (A).

Example:

1. Cardinality of empty set θ is 0 and is denoted by |θ| = 0
2. Sets of even positive integer is not a finite set.

A set is called a finite set if there is one to one correspondence between the elements in the set and the element in some set n, where n is a natural number and n is the cardinality of the set. Finite Sets are also called numerable sets. n is termed as the cardinality of sets or a cardinal number of sets.

2. Infinite Sets: A set which is not finite is called as Infinite Sets.

Countable Infinite: If there is one to one correspondence between the elements in set and element in N. A countably infinite set is also known as Denumerable. A set that is either finite or denumerable is known as countable. A set which is not countable is known as Uncountable. The set of a non-negative even integer is countable Infinite.

Uncountable Infinite: A set which is not countable is called Uncountable Infinite Set or non-denumerable set or simply Uncountable.

Example: Set R of all +ve real numbers less than 1 that can be represented by the decimal form 0. a₁,a₂,a₃..... Where a₁ is an integer such that 0 ≤ a_i ≤ 9.

3. Subsets: If every element in a set A is also an element of a set B, then A is called a subset of B. It can be denoted as A ⊆ B. Here B is called Superset of A.

Example: If A= {1, 2} and B= {4, 2, 1} the A is the subset of B or A ⊆ B.

Properties of Subsets:

1. Every set is a subset of itself.
2. The Null Set i.e.∅ is a subset of every set.
3. If A is a subset of B and B is a subset of C, then A will be the subset of C. If A⊂B and B⊂ C ⟹ A ⊂ C
4. A finite set having n elements has 2ⁿ subsets.

4. Proper Subset: If A is a subset of B and A ≠ B then A is said to be a proper subset of B. If A is a proper subset of B then B is not a subset of A, i.e., there is at least one element in B which is not in A.

Example:

(i) Let A = {2, 3, 4}
B = {2, 3, 4, 5}

A is a proper subset of B.

(ii) The null ∅ is a proper subset of every set.

5. Improper Subset: If A is a subset of B and A = B, then A is said to be an improper subset of B.

Example

(i) A = {2, 3, 4}, B = {2, 3, 4}

A is an improper subset of B.

(ii) Every set is an improper subset of itself.

6. Universal Set: If all the sets under investigations are subsets of a fixed set U, then the set U is called Universal Set.

Example: In the human population studies the universal set consists of all the people in the world.

7. Null Set or Empty Set: A set having no elements is called a Null set or void set. It is denoted by∅.

8. Singleton Set: It contains only one element. It is denoted by {s}.

Example: S= {x|x∈N, 7<x<9} = {8}

9. Equal Sets: Two sets A and B are said to be equal and written as A = B if both have the same elements. Therefore, every element which belongs to A is also an element of the set B and every element which belongs to the set B is also an element of the set A.

1. A = B ⟺ {x ϵ A  ⟺  x ϵ B}.  

If there is some element in set A that does not belong to set B or vice versa then A ≠ B, i.e., A is not equal to B.

10. Equivalent Sets: If the cardinalities of two sets are equal, they are called equivalent sets.

Example: If A= {1, 2, 6} and B= {16, 17, 22}, they are equivalent as cardinality of A is equal to the cardinality of B. i.e. |A|=|B|=3

11. Disjoint Sets: Two sets A and B are said to be disjoint if no element of A is in B and no element of B is in A.

Example:

R = {a, b, c}
S = {k, p, m}

R and S are disjoint sets.

12. Power Sets: The power of any given set A is the set of all subsets of A and is denoted by P (A). If A has n elements, then P (A) has 2ⁿ elements.

Example: A = {1, 2, 3}
P (A) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.

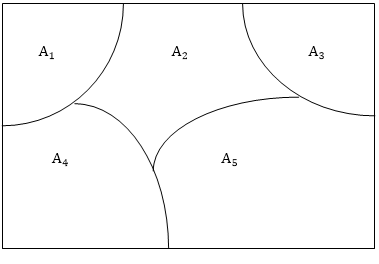
Partitions of a Set:

Let S be a nonempty set. A partition of S is a subdivision of S into nonoverlapping, nonempty subsets. Speceficially, a partition of S is a collection {Ai} of nonempty subsets of S such that:

• Each a in S belongs to one of the Ai.
• The sets of {Ai} are mutually disjoint; that is,

Aj≠ Ak Then Aj ∩ Ak= ∅

The subsets in a partition are called cells.

Fig: Venn diagram of a partition of the rectangular set S of points into five cells,A₁,A₂,A₃,A₄,A₅

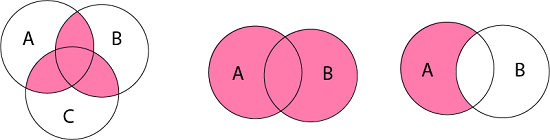
Venn Diagrams:

Venn diagram is a pictorial representation of sets in which an enclosed area in the plane represents sets.

Examples: