Vertex Cover

A Vertex Cover of a graph G is a set of vertices such that each edge in G is incident to at least one of these vertices.

The decision vertex-cover problem was proven NPC. Now, we want to solve the optimal version of the vertex cover problem, i.e., we want to find a minimum size vertex cover of a given graph. We call such vertex cover an optimal vertex cover C*.

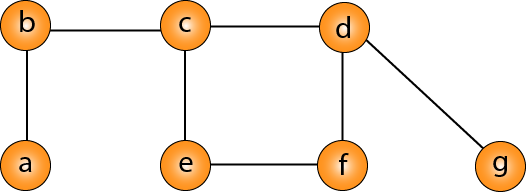
An approximate algorithm for vertex cover:

1. Approx-Vertex-Cover (G = (V, E))  
2. {             
3.        C = empty-set;  
4.     E'= E;  
5.     While E' is not empty do  
6.       {  
7.     Let (u, v) be any edge in E': (*)  
8.     Add u and v to C;  
9.     Remove from E' all edges incident to  
10.        u or v;  
11.       }  
12.     Return C;  
13. }  

The idea is to take an edge (u, v) one by one, put both vertices to C, and remove all the edges incident to u or v. We carry on until all edges have been removed. C is a VC. But how good is C?

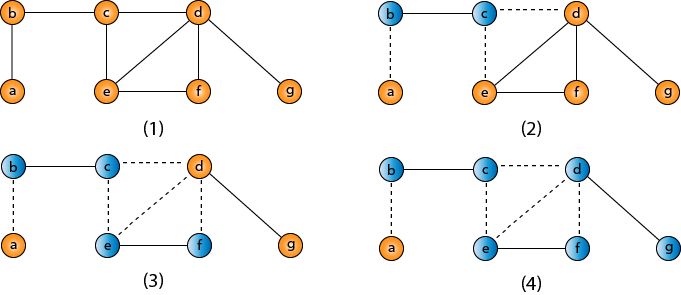
VC = {b, c, d, e, f, g}