Genetic Algorithms

Genetic Algorithms

Genetic Algorithms(GAs) are adaptive heuristic search algorithms that belong to the larger part of evolutionary algorithms. Genetic algorithms are based on the ideas of natural selection and genetics. These are intelligent exploitation of random search provided with historical data to direct the search into the region of better performance in solution space. They are commonly used to generate high-quality solutions for optimization problems and search problems.

Genetic algorithms simulate the process of natural selection which means those species who can adapt to changes in their environment are able to survive and reproduce and go to next generation. In simple words, they simulate “survival of the fittest” among individual of consecutive generation for solving a problem. Each generation consist of a population of individuals and each individual represents a point in search space and possible solution. Each individual is represented as a string of character/integer/float/bits. This string is analogous to the Chromosome.

Foundation of Genetic Algorithms

Genetic algorithms are based on an analogy with genetic structure and behavior of chromosomes of the population. Following is the foundation of GAs based on this analogy –  

1. Individual in population compete for resources and mate
2. Those individuals who are successful (fittest) then mate to create more offspring than others
3. Genes from “fittest” parent propagate throughout the generation, that is sometimes parents create offspring which is better than either parent.
4. Thus each successive generation is more suited for their environment.

Search space

The population of individuals are maintained within search space. Each individual represents a solution in search space for given problem. Each individual is coded as a finite length vector (analogous to chromosome) of components. These variable components are analogous to Genes. Thus a chromosome (individual) is composed of several genes (variable components). 

Fitness Score

A Fitness Score is given to each individual which shows the ability of an individual to “compete”. The individual having optimal fitness score (or near optimal) are sought. 

The GAs maintains the population of n individuals (chromosome/solutions) along with their fitness scores.The individuals having better fitness scores are given more chance to reproduce than others. The individuals with better fitness scores are selected who mate and produce better offspring by combining chromosomes of parents. The population size is static so the room has to be created for new arrivals. So, some individuals die and get replaced by new arrivals eventually creating new generation when all the mating opportunity of the old population is exhausted. It is hoped that over successive generations better solutions will arrive while least fit die. 

Each new generation has on average more “better genes” than the individual (solution) of previous generations. Thus each new generations have better “partial solutions” than previous generations. Once the offspring produced having no significant difference from offspring produced by previous populations, the population is converged. The algorithm is said to be converged to a set of solutions for the problem.

GA cycle of reproduction

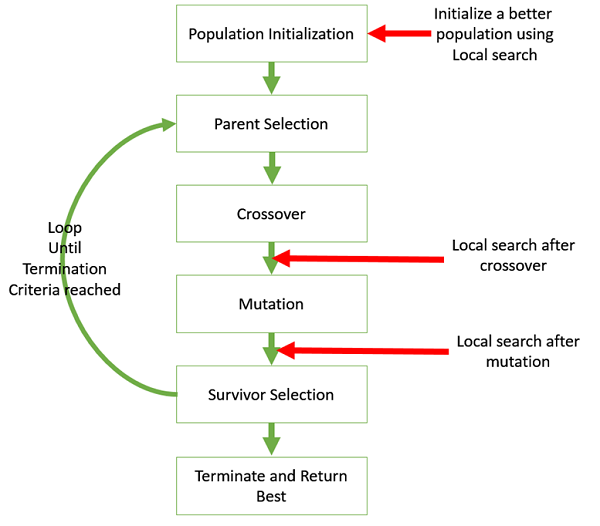
Components of Genetic Algorithms

Once the initial generation is created, the algorithm evolves the generation using following operators – 

1. Crossover

The crossover operator is analogous to reproduction and biological crossover. In this more than one parent is selected and one or more off-springs are produced using the genetic material of the parents. Crossover is usually applied in a GA with a high probability – pc .

Crossover Operators

In this section we will discuss some of the most popularly used crossover operators. It is to be noted that these crossover operators are very generic and the GA Designer might choose to implement a problem-specific crossover operator as well.

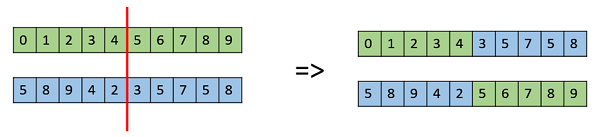
One Point Crossover

In this one-point crossover, a random crossover point is selected and the tails of its two parents are swapped to get new off-springs.

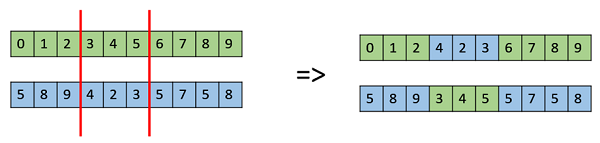
Multi Point Crossover

Multi point crossover is a generalization of the one-point crossover wherein alternating segments are swapped to get new off-springs.

Uniform Crossover

In a uniform crossover, we don’t divide the chromosome into segments, rather we treat each gene separately. In this, we essentially flip a coin for each chromosome to decide whether or not it’ll be included in the off-spring. We can also bias the coin to one parent, to have more genetic material in the child from that parent.

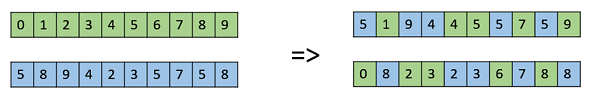
Whole Arithmetic Recombination

This is commonly used for integer representations and works by taking the weighted average of the two parents by using the following formulae −

• Child1 = α.x + (1-α).y
• Child2 = α.x + (1-α).y

Obviously, if α = 0.5, then both the children will be identical as shown in the following image.

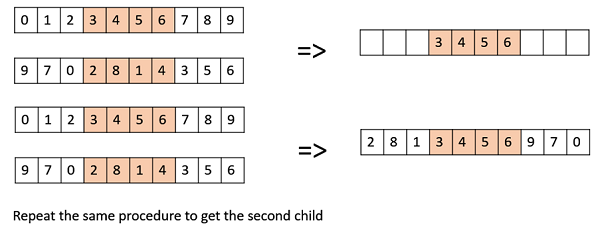
Davis’ Order Crossover (OX1)

OX1 is used for permutation based crossovers with the intention of transmitting information about relative ordering to the off-springs. It works as follows −

• Create two random crossover points in the parent and copy the segment between them from the first parent to the first offspring.

• Now, starting from the second crossover point in the second parent, copy the remaining unused numbers from the second parent to the first child, wrapping around the list.

• Repeat for the second child with the parent’s role reversed.

There exist a lot of other crossovers like Partially Mapped Crossover (PMX), Order based crossover (OX2), Shuffle Crossover, Ring Crossover, etc.

 2. Mutation

In simple terms, mutation may be defined as a small random tweak in the chromosome, to get a new solution. It is used to maintain and introduce diversity in the genetic population and is usually applied with a low probability – pm. If the probability is very high, the GA gets reduced to a random search.

Mutation is the part of the GA which is related to the “exploration” of the search space. It has been observed that mutation is essential to the convergence of the GA while crossover is not.

Mutation Operators

In this section, we describe some of the most commonly used mutation operators. Like the crossover operators, this is not an exhaustive list and the GA designer might find a combination of these approaches or a problem-specific mutation operator more useful.

Bit Flip Mutation

In this bit flip mutation, we select one or more random bits and flip them. This is used for binary encoded GAs.

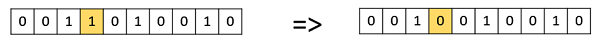
Random Resetting

Random Resetting is an extension of the bit flip for the integer representation. In this, a random value from the set of permissible values is assigned to a randomly chosen gene.

Swap Mutation

In swap mutation, we select two positions on the chromosome at random, and interchange the values. This is common in permutation based encodings.

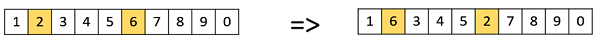
Scramble Mutation

Scramble mutation is also popular with permutation representations. In this, from the entire chromosome, a subset of genes is chosen and their values are scrambled or shuffled randomly.

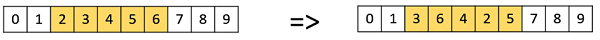
Inversion Mutation

In inversion mutation, we select a subset of genes like in scramble mutation, but instead of shuffling the subset, we merely invert the entire string in the subset.

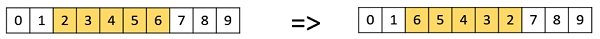
The whole algorithm can be summarized as –  

1) Randomly initialize populations p
2) Determine fitness of population
3) Until convergence repeat:
      a) Select parents from population
      b) Crossover and generate new population
      c) Perform mutation on new population
      d) Calculate fitness for new population

Example problem and solution using Genetic Algorithms

Given a target string, the goal is to produce target string starting from a random string of the same length. In the following implementation, following analogies are made – 

• Characters A-Z, a-z, 0-9, and other special symbols are considered as genes
• A string generated by these characters is considered as chromosome/solution/Individual

Fitness score is the number of characters which differ from characters in target string at a particular index. So individual having lower fitness value is given more preference.