Derivation Tree

Derivation tree is a graphical representation for the derivation of the given production rules for a given CFG. It is the simple way to show how the derivation can be done to obtain some string from a given set of production rules. The derivation tree is also called a parse tree.

Parse tree follows the precedence of operators. The deepest sub-tree traversed first. So, the operator in the parent node has less precedence over the operator in the sub-tree.

A parse tree contains the following properties:

1. The root node is always a node indicating start symbols.
2. The derivation is read from left to right.
3. The leaf node is always terminal nodes.
4. The interior nodes are always the non-terminal nodes.

Example 1:

Production rules:

E = E + E  

E = E * E  

E = a | b | c  

Input

a * b + c  

Step 1:

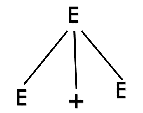
Step 2:

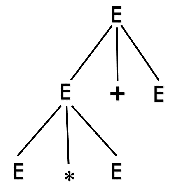
Step 2:

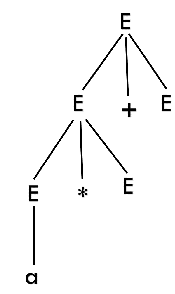
Step 4:

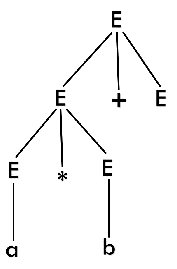
Step 5:

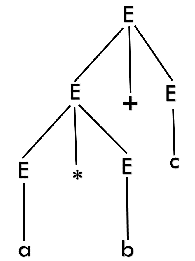
Note: We can draw a derivation tree step by step or directly in one step.

Example 2:

Draw a derivation tree for the string "bab" from the CFG given by

S → bSb | a | b  

Solution:

Now, the derivation tree for the string "bbabb" is as follows:

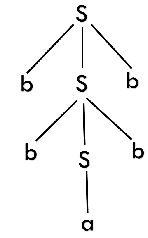
The above tree is a derivation tree drawn for deriving a string bbabb. By simply reading the leaf nodes, we can obtain the desired string. The same tree can also be denoted by,

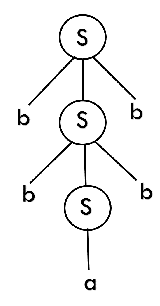
Example 3:

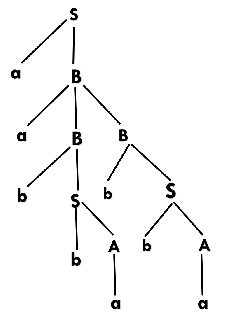
Construct a derivation tree for the string aabbabba for the CFG given by,

S → aB | bA  

A → a | aS | bAA  

B → b | bS | aBB  

Solution:

To draw a tree, we will first try to obtain derivation for the string aabbabba

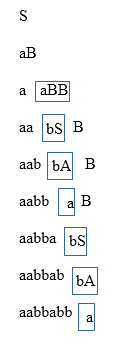
Now, the derivation tree is as follows:

Example 4:

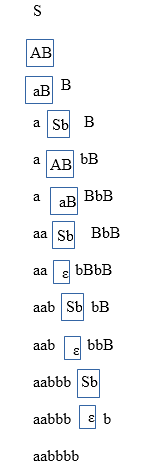
Show the derivation tree for string "aabbbb" with the following grammar.

S → AB | ε  

A → aB  

B → Sb  

Solution:

To draw a tree we will first try to obtain derivation for the string aabbbb

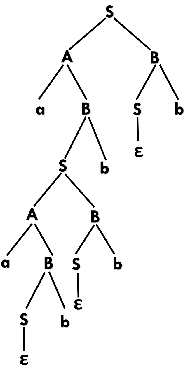
Now, the derivation tree for the string "aabbbb" is as follows: