DFA (Deterministic finite automata)

• DFA refers to deterministic finite automata. Deterministic refers to the uniqueness of the computation. The finite automata are called deterministic finite automata if the machine is read an input string one symbol at a time.
• In DFA, there is only one path for specific input from the current state to the next state.
• DFA does not accept the null move, i.e., the DFA cannot change state without any input character.
• DFA can contain multiple final states. It is used in Lexical Analysis in Compiler.

In the following diagram, we can see that from state q0 for input a, there is only one path which is going to q1. Similarly, from q0, there is only one path for input b going to q2.

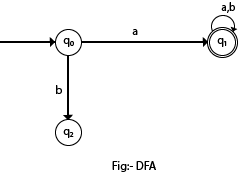
Formal Definition of DFA

A DFA can be expressed by the same 5-tuple (Q, ∑, δ, q0, F) that we used to express Finite Automata where:

1. Q: Set of finite states (for eg: {q0,q1,q2,……,qf})
2. Σ: Set of symbols (for eg: a,b....1,0…..)
3. 𝛿: Transition Function (function applied/ condition applied onto the string)
4. q0: Initial/start state
5. F: Set of final states (here, qf but there can be multiple final states)

 

Each input symbol must have one transition for each state.

The transition function can be defined as δ: Q x ∑→Q.

Graphical Representation of DFA

Graphical Representation of DFA is called state diagram

• The vertices represent the states.
• The arrow (à) labeled with an input alphabet (∑) show the transitions (δ).
• The initial state (q0) is denoted by a circle with single incoming arrow.
• The final state is denoted by double circles.

Following figure shows all

Need of DFA

DFAs make it much easier to use certain projects and applications that switch between valid and invalid states. DFAs are useful in the functionality of applications such as

• Vending Machines
• Traffic Lights
• Video Games
• Text Parsing
• Regular Expression Matching
• CPU Controllers
• Protocol Analysis
• Natural Language Processing
• Speech Recognition

Properties of DFA

Properties of DFA are:

• If a Language L is a Regular Language, then there must be a Deterministic Finite Automaton M such that L(M) = L.
• If Language L is a Regular Language, then the Language ~L (complement of L) is also a Regular Language. So, if there is a Deterministic Finite Automaton M for L, there exists another Deterministic Finite Automaton N for ~L.
• A model of Computation is called Deterministic if there is only one choice at every step for a given input. It can be modeled using Deterministic Finite Automaton (DFA).
• Deterministic Finite Automaton is always complete that is transition from every state has been defined for every possible input.
• DFA is closed under the following operation:
• Union
• Intersection
• Concatenation
• Negation
• Kleene closure
• Reversal
• Quotient
• Substitution
• Homomorphism

Construction of DFA

Suppose we are going to construct a DFA which accept a language of all strings, end with “a” and input sigma (∑) = {0, 1}. Then,

1. First draw all possible strings of that language.

L= {a, aa, aaa, ba, baba, aba, bbbba……….}

Note: epsilon and those strings which are ending with b (i.e. aabab) are not accepted.

2. For each sigma value (0, 1…n) there must be a provided path from each state (q0, q1, q2….qn).

Possibilities of path for each input from a any state

• May Go to next state if exist
• Self-loop
• Go to trap state
• May Go to previous state if exist

3. Now Draw the Automata model which will always according to generated language. Automata machine must accept the strings of given language (i.e. minimum length string to last maximum string).,

Steps for Construction of DFA

Let construct DFA for language L= {a, aa, aaa, ba, baba, aba, bbbba……….}

Step 01: As Minimum length string is “a” which will be accepted as

Step 02: At initial state (q0), the path for input “a” is provided.  There must be a path for input “b” from initial state (q0).

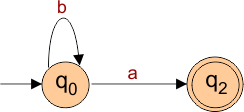
Step 03: Now in the same way q1 must tell the path against each input  value of sigma “a” and “b” .  So final DFA which will accept all the strings of given language is given below

Example 1: Design a DFA over the input alphabets {a,b} which accepts all strings that end with a.

Step 1: Consider the strings {a, aa, ba, aba, bba………} that follow the above condition. We can derive from the preceding example that any number of alphabets can come before a.

Step 2: Design the DFA for the lowest possible string.

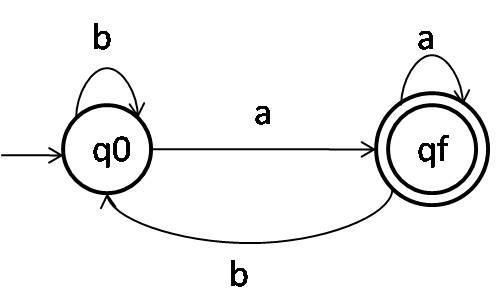
As we can see, in order to answer the question, we need a machine that accepts strings that end in a, it doesn’t matter what is the starting of the string, only the ending string should be a. Because our condition only involves one symbol, we have only one necessary transition, so we take two states. In this case, the string can begin with any symbol but must end with an a. As a result, any presence of b is directed to q0, which is our initial state, whereas a's are directed to the final state qf, which is the final state of the DFA.

The transition table for the above DFA is as followed:

Dead state in DFA

If the machine has successfully progressed to the final string accepting state, we can say that the string has been accepted by the DFA.

However, if we arrive at a point where the machine can no longer progress to its final state, we have arrived at a dead state. A Dummy state is another name for a dead state.

Let us look at the following example to understand the dead state in a better way

 

In this example, the machine will begin, and if we want to read strings that begin with 0, the machine will reach its final state B, which will allow it to accept a string.

However, if we start the machine with 1, it will not be able to advance to the final state. It will reach another intermediate state which is C. We are now in a dead state after reading 1. And the string will not be accepted by DFA.

The transition table for the above DFA is as followed:

Example 2: DFA with ∑ = {0, 1} accepts all starting with 0.

Solution:

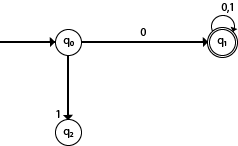
Explanation: In the above diagram, we can see that on given 0 as input to DFA in state q0 the DFA changes state to q1 and always go to final state q1 on starting input 0. It can accept 00, 01, 000, 001....etc. It can't accept any string which starts with 1, because it will never go to final state on a string starting with 1.

Example 3: DFA with ∑ = {0, 1} accepts all ending with 0.

Solution:

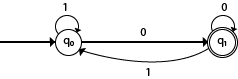
Explanation:

In the above diagram, we can see that on given 0 as input to DFA in state q0, the DFA changes state to q1. It can accept any string which ends with 0 like 00, 10, 110, 100....etc. It can't accept any string which ends with 1, because it will never go to the final state q1 on 1 input, so the string ending with 1, will not be accepted or will be rejected.