Unambiguous Grammar

A grammar can be unambiguous if the grammar does not contain ambiguity that means if it does not contain more than one leftmost derivation or more than one rightmost derivation or more than one parse tree for the given input string.

To convert ambiguous grammar to unambiguous grammar, we will apply the following rules:

1. If the left associative operators (+, -, *, /) are used in the production rule, then apply left recursion in the production rule. Left recursion means that the leftmost symbol on the right side is the same as the non-terminal on the left side. For example,

X → Xa  

2. If the right associative operates(^) is used in the production rule then apply right recursion in the production rule. Right recursion means that the rightmost symbol on the left side is the same as the non-terminal on the right side. For example,

X → aX  

Example 1:

Consider a grammar G is given as follows:

S → AB | aaB  

A → a | Aa  

B → b  

Determine whether the grammar G is ambiguous or not. If G is ambiguous, construct an unambiguous grammar equivalent to G.

Solution:

Let us derive the string "aab"

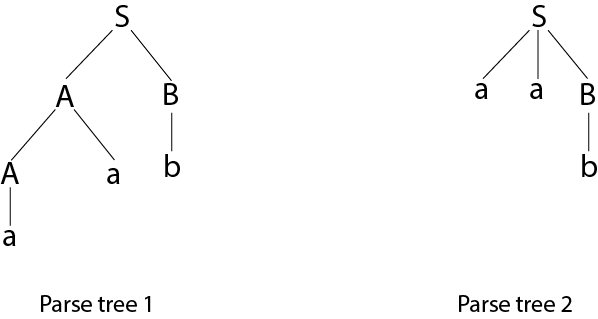
As there are two different parse tree for deriving the same string, the given grammar is ambiguous.

Unambiguous grammar will be:

S → AB  

A → Aa | a  

B → b  

Example 2:

Show that the given grammar is ambiguous. Also, find an equivalent unambiguous grammar.

S → ABA  

A → aA | ε  

B → bB | ε  

Solution:

The given grammar is ambiguous because we can derive two different parse tree for string aa.

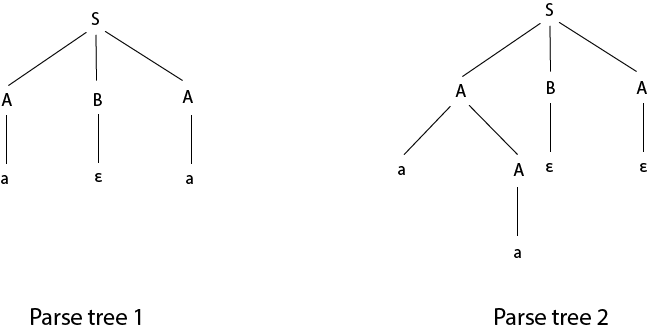
The unambiguous grammar is:

S → aXY | bYZ | ε  

Z → aZ | a  

X → aXY | a | ε  

Y → bYZ | b | ε 

Example 3:

Show that the given grammar is ambiguous. Also, find an equivalent unambiguous grammar.

E → E + E  

E → E * E  

E → id  

Solution:

Let us derive the string "id + id * id"

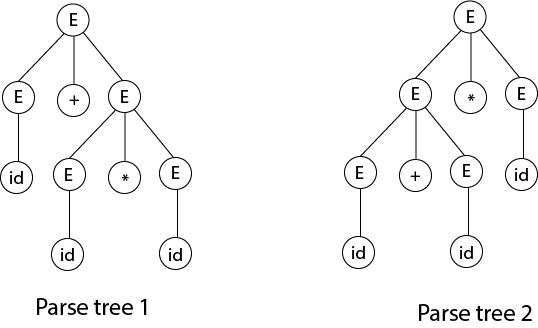
As there are two different parse tree for deriving the same string, the given grammar is ambiguous.

Unambiguous grammar will be:

E → E + T  

E → T  

T → T * F  

T → F  

F → id  

Example 4:

Check that the given grammar is ambiguous or not. Also, find an equivalent unambiguous grammar.

S → S + S  

S → S * S  

S → S ^ S  

S → a  

Solution:

The given grammar is ambiguous because the derivation of string aab can be represented by the following string:

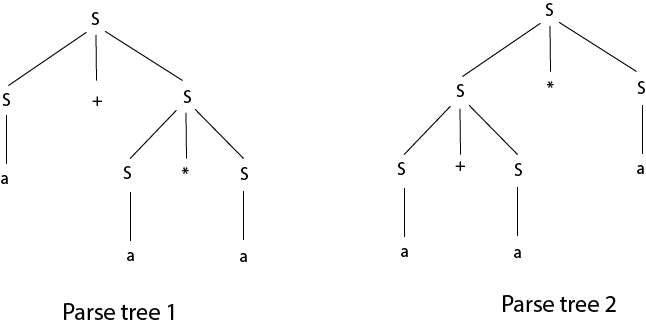
Unambiguous grammar will be:

S → S + A |  

A → A * B | B  

B → C ^ B | C  

C → a