Introduction to Undecidability

In the theory of computation, we often come across such problems that are answered either 'yes' or 'no'. The class of problems which can be answered as 'yes' are called solvable or decidable. Otherwise, the class of problems is said to be unsolvable or undecidable.

Undecidability of Universal Languages:

The universal language L_u is a recursively enumerable language and we have to prove that it is undecidable (non-recursive).

Theorem: L_u is RE but not recursive.

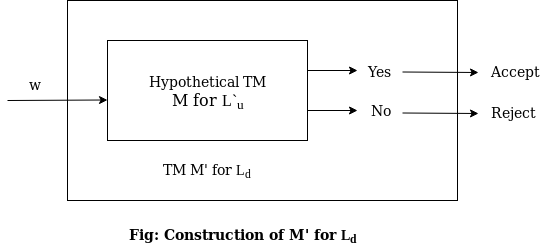
Proof: Consider that language L_u is recursively enumerable language. We will assume that L_u is recursive. Then the complement of L_u that is L`u is also recursive. However, if we have a TM M to accept L`u then we can construct a TM L_d. But L_d the diagonalization language is not RE. Thus our assumption that L_u is recursive is wrong (not RE means not recursive). Hence we can say that L_u is RE but not recursive. The construction of M for L_d is as shown in the following diagram: