Two stack Pushdown Automata

Two stacks push down automata (PDA) includes the following factors −

• A Turing machine can accept languages that are not accepted by any PDA with one stack.
• The strength of pushdown automata is increased by adding extra stacks.
• A PDA with two stacks has the same computation power as for a Turing Machine.

Two-Stack PDA is a computational model which is based on the generalization of Pushdown Automata (PDA) and Non-deterministic Two-Stack PDA which is equivalent to a deterministic Two-Stack PDA.

The moves of the Two-Stack PDA are based on the following −

• The state of finite control.
• The input symbol that reads.
• The top of the stack symbol on each of its stacks.

Some of the characteristics of the Turing Machine (TM) and the Two-stack Push down automaton (Two-stack PDA) Machine are as follows −

Turing Machine	Two-stack PDA Machine
Change state.	Change state.
Write a tape symbol in cell scanned.	The input symbol read.
Move the head left or right.	Replace the symbol of each stack with a string of zero or more stack symbols.

The diagram given below is of the TM variant Two-stack PDA machine.

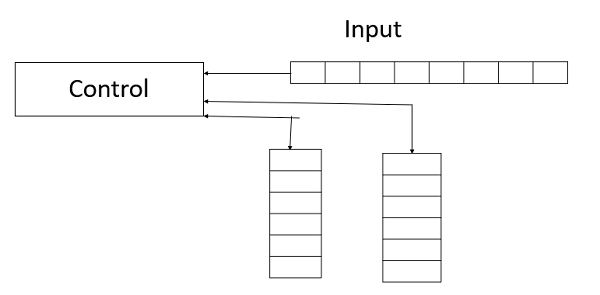
The right half of the tape is kept on one stack, and the left half on the other.

As we move along, we pop characters off one and push them onto the other.

Example: 

2- Stack PDA for L= {an bn cn | n1}

            = {abc, aabbcc, aaabbbccc, aaaabbbbcccc, . . . . . . . . }

Logic to design 2-Stack PDA: 

If a is read, push a in Stack 1, No change in Stack 2 

If b is read, pop a from Stack1 and push b into Stack 2 // this ensures number of a = b

If c is read, pop b from Stack 2 // this ensures number of b = c

Transition Function:

We assume Z01 and Z02 as initial symbols placed in Stack1 and Stack 2 respectively

δ(q0, a, Z01 , Z02 )= δ(q1, aZ01 , Z02 )  //when a is read, State is changed, Push a into Stack1 and Stack2 has Z02

δ(q1, a, a , Z02 ) = δ(q1, aa , Z02 )  // when a is read, Push a into Stack1 and Stack2 is unchanged

δ(q1, b, a , Z02 ) = δ(q2, ε , bZ02 ) // when b is read, State is changed,  Pop a from Stack1 and Push b in Stack2

δ(q2, b, a , b ) = δ(q2, ε , bb )  //when b is read, Pop a from Stack1 and Push b in Stack2

δ(q2, c, Z01 , b ) = δ(q3, Z01 , ε ) when c is read, State is changed,  top of Stack1 has Z01 and pop b from Stack2

δ(q3, c, Z01 , b ) = δ(q3, Z01 , ε ) when c is read, State is changed,  top of Stack1 is unchanged and pop b from Stack2

δ(q3, ε, Z01 , Z02) = δ(qf, ε , ε ) //Acceptance by Empty Stack