This algorithm is used for scan converting a line. It was developed by Bresenham. It is an efficient method because it involves only integer addition, subtractions, and multiplication operations. These operations can be performed very rapidly so lines can be generated quickly.
In this method, next pixel selected is that one who has the least distance from true line.
The method works as follows:
Assume a pixel P1'(x1',y1'),then select subsequent pixels as we work our may to the night, one pixel position at a time in the horizontal direction toward P2'(x2',y2').
Once a pixel in choose at any step
The next pixel is
- Either the one to its right (lower-bound for the line)
- One top its right and up (upper-bound for the line)
The line is best approximated by those pixels that fall the least distance from the path between P1',P2'.
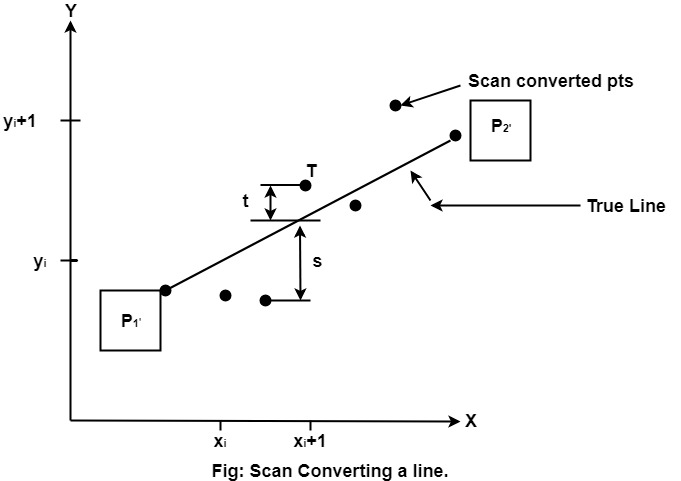
To chooses the next one between the bottom pixel S and top pixel T.
If S is chosen
We have xi+1=xi+1 and yi+1=yi
If T is chosen
We have xi+1=xi+1 and yi+1=yi+1
The actual y coordinates of the line at x = xi+1is
y=mxi+1+b
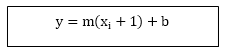
The distance from S to the actual line in y direction
s = y-yi
The distance from T to the actual line in y direction
t = (yi+1)-y
Now consider the difference between these 2 distance values
s - t
When (s-t) <0 ⟹ s < t
The closest pixel is S
When (s-t) ≥0 ⟹ s < t
The closest pixel is T
This difference is
s-t = (y-yi)-[(yi+1)-y]
= 2y - 2yi -1
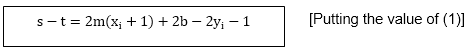
Substituting m by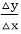 
and introducing decision variable
di=△x (s-t)
di=△x (2 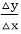(xi+1)+2b-2yi-1)
=2△xyi-2△y-1△x.2b-2yi△x-△x
di=2△y.xi-2△x.yi+c
Where c= 2△y+△x (2b-1)
We can write the decision variable di+1 for the next slip on
di+1=2△y.xi+1-2△x.yi+1+c
di+1-di=2△y.(xi+1-xi)- 2△x(yi+1-yi)
Since x_(i+1)=xi+1,we have
di+1+di=2△y.(xi+1-xi)- 2△x(yi+1-yi)
Special Cases
If chosen pixel is at the top pixel T (i.e., di≥0)⟹ yi+1=yi+1
di+1=di+2△y-2△x
If chosen pixel is at the bottom pixel T (i.e., di<0)⟹ yi+1=yi
di+1=di+2△y
Finally, we calculate d1
d1=△x[2m(x1+1)+2b-2y1-1]
d1=△x[2(mx1+b-y1)+2m-1]
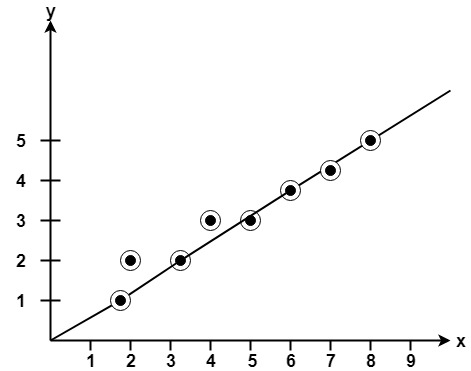
Since mx1+b-yi=0 and m = 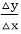, we have
d1=2△y-△x
Advantage:
1. It involves only integer arithmetic, so it is simple.
2. It avoids the generation of duplicate points.
3. It can be implemented using hardware because it does not use multiplication and division.
4. It is faster as compared to DDA (Digital Differential Analyzer) because it does not involve floating point calculations like DDA Algorithm.
Disadvantage:
1. This algorithm is meant for basic line drawing only Initializing is not a part of Bresenham's line algorithm. So to draw smooth lines, you should want to look into a different algorithm.
Bresenham's Line Algorithm:
Step1: Start Algorithm
Step2: Declare variable x1,x2,y1,y2,d,i1,i2,dx,dy
Step3: Enter value of x1,y1,x2,y2
Where x1,y1are coordinates of starting point
And x2,y2 are coordinates of Ending point
Step4: Calculate dx = x2-x1
Calculate dy = y2-y1
Calculate i1=2*dy
Calculate i2=2*(dy-dx)
Calculate d=i1-dx
Step5: Consider (x, y) as starting point and xendas maximum possible value of x.
If dx < 0
Then x = x2
y = y2
xend=x1
If dx > 0
Then x = x1
y = y1
xend=x2
Step6: Generate point at (x,y)coordinates.
Step7: Check if whole line is generated.
If x > = xend
Stop.
Step8: Calculate co-ordinates of the next pixel
If d < 0
Then d = d + i1
If d ≥ 0
Then d = d + i2
Increment y = y + 1
Step9: Increment x = x + 1
Step10: Draw a point of latest (x, y) coordinates
Step11: Go to step 7
Step12: End of Algorithm
Example: Starting and Ending position of the line are (1, 1) and (8, 5). Find intermediate points.
Solution: x1=1
y1=1
x2=8
y2=5
dx= x2-x1=8-1=7
dy=y2-y1=5-1=4
I1=2* ∆y=2*4=8
I2=2*(∆y-∆x)=2*(4-7)=-6
d = I1-∆x=8-7=1
|
x |
y |
d=d+I1 or
I2 |
|
1 |
1 |
d+I2=1+(-6)=-5 |
|
2 |
2 |
d+I1=-5+8=3 |
|
3 |
2 |
d+I2=3+(-6)=-3 |
|
4 |
3 |
d+I1=-3+8=5 |
|
5 |
3 |
d+I2=5+(-6)=-1 |
|
6 |
4 |
d+I1=-1+8=7 |
|
7 |
4 |
d+I2=7+(-6)=1 |
|
8 |
5 |
Program to implement Bresenham's Line Drawing Algorithm:
#include<stdio.h>
#include<graphics.h>
void drawline(int x0, int y0, int x1, int y1)
{
int dx, dy, p, x, y;
dx=x1-x0;
dy=y1-y0;
x=x0;
y=y0;
p=2*dy-dx;
while(x<x1)
{
if(p>=0)
{
putpixel(x,y,7);
y=y+1;
p=p+2*dy-2*dx;
}
else
{
putpixel(x,y,7);
p=p+2*dy;}
x=x+1;
}
}
int main()
{
int gdriver=DETECT, gmode, error, x0, y0, x1, y1;
initgraph(&gdriver, &gmode, "c:\\turboc3\\bgi");
printf("Enter co-ordinates of first point: ");
scanf("%d%d", &x0, &y0);
printf("Enter co-ordinates of second point: ");
scanf("%d%d", &x1, &y1);
drawline(x0, y0, x1, y1);
return 0;
}
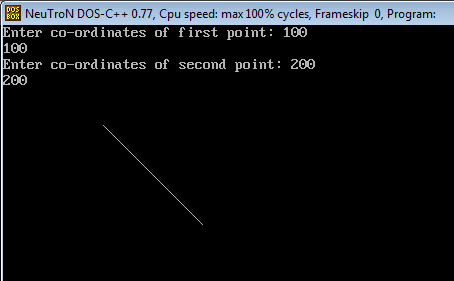
Output:
Differentiate between DDA Algorithm and Bresenham's Line Algorithm:
|
DDA Algorithm |
Bresenham's Line
Algorithm |
|
1. DDA Algorithm use
floating point, i.e., Real Arithmetic. |
1. Bresenham's Line
Algorithm use fixed point, i.e., Integer Arithmetic |
|
2. DDA Algorithms
uses multiplication & division its operation |
2.Bresenham's Line
Algorithm uses only subtraction and addition its operation |
|
3. DDA Algorithm is
slowly than Bresenham's Line Algorithm in line drawing because it uses real
arithmetic (Floating Point operation) |
3. Bresenham's
Algorithm is faster than DDA Algorithm in line because it involves only
addition & subtraction in its calculation and uses only integer
arithmetic. |
|
4. DDA Algorithm is
not accurate and efficient as Bresenham's Line Algorithm. |
4. Bresenham's Line
Algorithm is more accurate and efficient at DDA Algorithm. |
|
5.DDA Algorithm can
draw circle and curves but are not accurate as Bresenham's Line Algorithm |
5. Bresenham's Line
Algorithm can draw circle and curves with more accurate than DDA Algorithm. |
0 Comments