circle using Polynomial Method

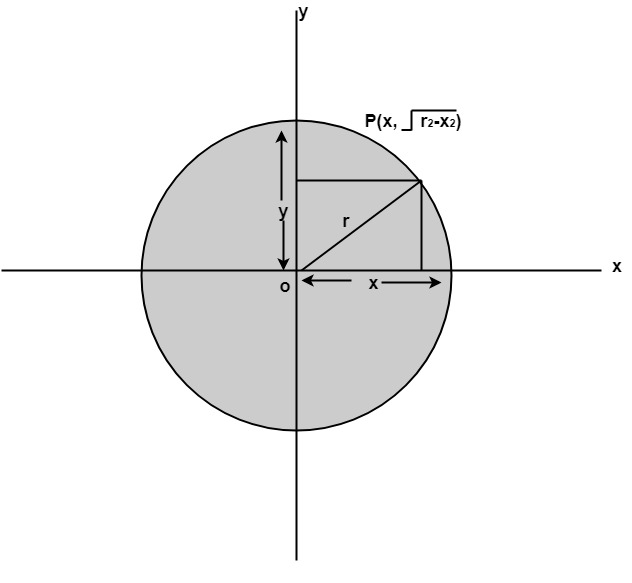
The first method defines a circle with the second-order polynomial equation as shown in fig:

                    y²=r²-x²
Where x = the x coordinate
          y = the y coordinate
          r = the circle radius

With the method, each x coordinate in the sector, from 90° to 45°, is found by stepping x from 0 to 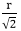 & each y coordinate is found by evaluating  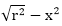for each step of x.

Algorithm:

Step1: Set the initial variables
          r = circle radius
          (h, k) = coordinates of circle center
                x=o
                I = step size
                x_end=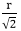 

Step2: Test to determine whether the entire circle has been scan-converted.

If x > x_end then stop.

Step3: Compute y =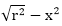 

Step4: Plot the eight points found by symmetry concerning the center (h, k) at the current (x, y) coordinates.

                Plot (x + h, y +k)          Plot (-x + h, -y + k)
                Plot (y + h, x + k)          Plot (-y + h, -x + k)
                Plot (-y + h, x + k)          Plot (y + h, -x + k)
                Plot (-x + h, y + k)          Plot (x + h, -y + k)

Step5: Increment x = x + i

Step6: Go to step (ii).

Program to draw a circle using Polynomial Method:

#include<graphics.h>  
#include<conio.h>  
#include<math.h>  
voidsetPixel(int x, int y, int h, int k)  
{  
    putpixel(x+h, y+k, RED);  
    putpixel(x+h, -y+k, RED);  
    putpixel(-x+h, -y+k, RED);  
    putpixel(-x+h, y+k, RED);  
    putpixel(y+h, x+k, RED);  
    putpixel(y+h, -x+k, RED);  
    putpixel(-y+h, -x+k, RED);  
    putpixel(-y+h, x+k, RED);  
}  
main()  
{  
    intgd=0, gm,h,k,r;  
    double x,y,x2;  
    h=200, k=200, r=100;  
    initgraph(&gd, &gm, "C:\\TC\\BGI ");  
    setbkcolor(WHITE);  
    x=0,y=r;  
    x2 = r/sqrt(2);  
    while(x<=x2)  
    {  
        y = sqrt(r*r - x*x);  
        setPixel(floor(x), floor(y), h,k);  
        x += 1;  
    }  
    getch();  
    closegraph();  
    return 0;  
}

  

Output: