Cryptography

Nowadays, computing systems play a significant role in every aspect of human activity. Every marketing, software, banking, healthcare, and education application uses this computing technology. However, you might be curious about how businesses protect their data and maintain the privacy of their banking activities.

"Cryptography" is the answer to each of these questions. In today's connected world, sensitive information must be protected, which is why cryptography has influenced the current information age.

Additionally, Gmail data is secured using cryptography and is transmitted throughout Google data centers in an encrypted manner. Cryptography is therefore regarded as the essential component for protecting shared information.

Cryptography

Cryptography uses codes to protect data and communications so only the intended receivers can decode and understand them. Consequently, restricting access to information from outside parties.

"Crypto" indicates "hidden," and "graphy" indicates "writing," respectively. The techniques used in cryptography to secure data are based on mathematical principles and a set of rule-based calculations known as algorithms to modify signals in a way that makes them challenging to decode.

These algorithms generate cryptographic keys, create digital signatures, safeguard data privacy, enable online browsing on the Internet, and ensure the confidentiality of private transactions like credit and debit card payments.

History of Cryptography

Cryptography started with ciphers, the initial among which was the Caesar Cipher. Contrasted to modern algorithms for cryptography, ciphers were much simpler to decode, yet both employed plaintext and keys.

Though simple, the earliest forms of encryption were ciphers. Modern cryptosystems and algorithms are considerably more advanced. They employ numerous iterations of ciphers and encrypt the ciphertext of messages to ensure the most secure data transportation and storage.

Currently used cryptography techniques can potentially be irreversible, ensuring the message's security forever. The requirement for data to be safeguarded more securely than ever before has led to the development of more complex cryptography methods. Most early cryptographic ciphers and algorithms have been cracked, making them ineffective for data security.

It would sometimes take years or even decades to figure out the meaning of a single message, even though it is possible to interpret today's algorithms. Thus, the competition to develop newer and more powerful cryptographic techniques continues.

What is The Purpose of Cryptography?

Cryptography aims to keep data and messages private and inaccessible to possible threats or bad actors. It frequently works invisibly to encrypt and decrypt the data you send through email, social media, applications, and website interactions.

There are several uses for symmetric cryptography, including:

• Payment applications and card transactions
• Random number generation
• Verify the sender's signature to be sure they are who they claim they are

There are several uses for asymmetric cryptography, including:

• Email messages
• SIM card authentication
• Web security
• Exchange of private keys

Types of Cryptography

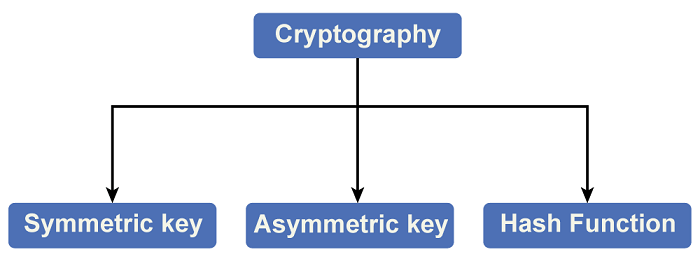
There are three main types of cryptography:

Symmetric key Cryptography: With the encryption technique, the sender and the recipient use the same shared key to encrypt and decrypt messages.

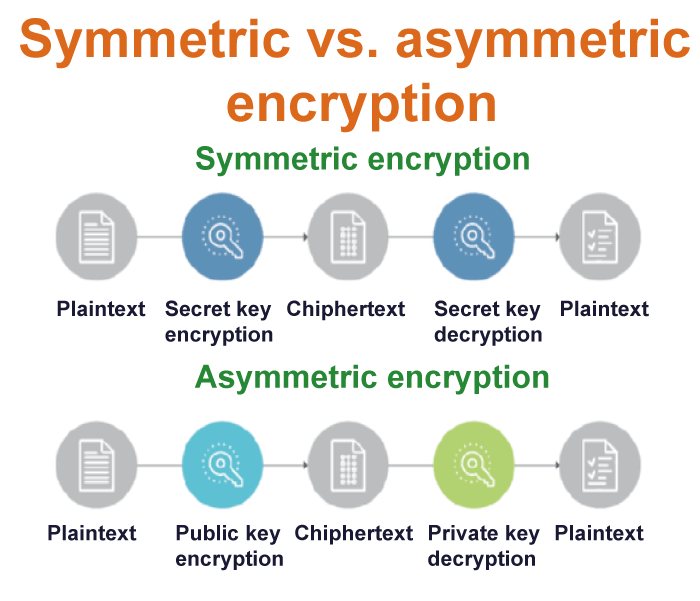
Although symmetric key systems are quicker and easier to use, they have the drawback of requiring a secure key exchange between the sender and the receiver. Data Encryption System (DES) is the most widely used symmetric key encryption method.

Hash Functions: In this algorithm, no key is used. The plain text is used to produce a hash value that has a fixed length, making it challenging to retrieve the plain text's information. Hash functions are widely used by operating systems to encrypt passwords.

Asymmetric Key Cryptography: This approach uses a set of keys to encrypt and decrypt data. Public keys are used for encryption, whereas private keys are used for decryption.

The Public Key and Private Key are different from one another. Even if everyone knows the public key, only the intended recipient may decode the message since only he can access the private key.

Techniques Used for Cryptography

In the age of computers, cryptography is frequently associated with converting plain text into cipher text, which is text that the intended recipient can only decode. This process is known as encryption. The process of converting encrypted text into plain text is called decryption.

Features of Cryptography

Cryptography has the following features:

• Confidentiality: The only person who can access information is the one it is intended for, which is the primary feature of cryptography.
• Integrity: Information cannot be altered while it is being stored or sent from the sender to the intended destination without the recipient spotting the addition of new information in Cryptography.
• Non-repudiation: The creator/sender of a message cannot deny his intent to send information at a future point.
• Authentication: The identities of the sender and the recipient have been confirmed. Furthermore, the information's source and final destination are confirmed.
• Availability: It also ensures that the required information is available to authorized users at the appropriate time.
• Key Management: The creation, distribution, storage, and alteration of cryptographic keys take place in this process.
• Algorithm: Mathematical formulae are used in cryptography to encrypt and decrypt messages.
• Digital Signatures: A signature that can be applied to messages to protect the message's authenticity and sender identification.

Cryptography vs. Cryptology

Cryptography refers to "secret writing," with the word "crypt" standing for "hidden" or "secret." While the terms cryptography and cryptology are sometimes used interchangeably, respectively, cryptology is the theory, and cryptography is the practice of composing secret messages.

Cryptology is defined as "knowledge of secrecy." Converting plaintext into ciphertext is known as encryption or "making secret." Although encryption is an integral component of cryptography, it does not cover the full field of science. The reverse of encryption is decryption.

The most important aspect of the encryption process is that it usually includes both an algorithm and a key. A key is only an extra bit of information?almost always a number?that describes how the plaintext will be treated when the algorithm encrypts it.

In a safe cryptographic system, even though you know the process by which a particular message is encrypted, it must be hard or impossible to decrypt without that key.

Encryption and Decryption

Cryptography involves two phases at its most fundamental level: Encryption and Decryption.

Encryption uses a cipher to encrypt and transform the plaintext into ciphertext. On the other hand, decryption transforms the ciphertext into plaintext by employing the same cipher.

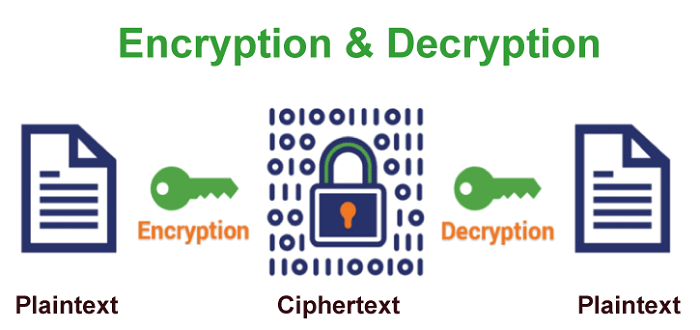
The most popular application of cryptography when sending electronic data is encrypting and decrypting emails and other plaintext messages. The simplest method is the "secret key" or symmetric approach.

The secret key is used to encrypt data, and after decoding, the secret key and encoded message are sent to the recipient. What is the problem, then? A third party is all they need to decode and analyze the message if it is intercepted.

Cryptologists developed the asymmetric or "public key" approach to solve this issue. Each user, in this case, has two keys: a private key and a public key. Senders request the recipient's public key before encrypting and sending the message.

Cryptographic Algorithms

Cryptosystems encrypt and decrypt information using cryptographic algorithms, or ciphers, to secure communications between computer systems, devices, and applications.

A cipher suite uses three different algorithms: one for encryption, message authentication, and key exchange. This process, integrated into protocols and developed using software that runs on operating systems (OS) and networked computer systems, involves:

• Data encryption and decryption using the production of public and private keys
• To authenticate messages, use digital signature and verification
• Key exchange

Advantages

Access Management: Access control can use cryptography to guarantee that only individuals with the appropriate authorizations are granted access to a resource. The resource is encrypted and can only be accessed by those with the proper decryption key.

Secure Communication: Cryptography is essential for private communication over the Internet. It provides safe methods for sending sensitive data like bank account numbers, passwords, and other private information over the Internet.

Protection against attacks: Attacks like replay and man-in-the-middle attacks can be defended against with the help of cryptography. It provides techniques for identifying and preventing these assaults.

Compliance with legal requirements: Businesses can use cryptography to help them deal with several legal obligations, such as data protection and privacy laws.

Applications of Cryptography

Computer passwords: Cryptography is frequently used in computer security, especially when creating and managing passwords. When users log in, their password is hashed and contrasted with the previously saved hash. To store them, passwords are first hashed and encrypted. This method encrypts the passwords so that even if hackers can access the password database, they can't comprehend the passwords.

Digital Currencies: Cryptography is also used by digital currencies like Bitcoin to secure transactions and prevent fraud. Since advanced algorithms and cryptographic keys safeguard transactions, tampering with or creating fake transactions is practically impossible.

Secure web browsing: Cryptography protects users from eavesdropping in on their conversations and man-in-the-middle attacks and provides online browsing security. The Secure Sockets Layer (SSL) and Transport Layer Security (TLS) protocols use public key cryptography to encrypt data between the web server and the client, creating a secure communication channel.

Digital signatures: Digital signatures are used to sign papers and act as the handwritten signature's digital copy. Cryptography is used to create digital signatures, and public key cryptography is used to verify them. Digital signatures are becoming more widely used, and many countries have laws that make them legally binding.

Authentication: When logging into a computer, cryptography is employed as the authentication method, for example, a bank account or a secure network. The authentication protocols use cryptographic techniques to validate the user's identity and possession of the necessary access privileges to the resource.

Cryptocurrencies: Cryptocurrencies like Bitcoin and Ethereum largely rely on cryptography to protect transactions, prevent fraud, and uphold the integrity of the network. Transactions are protected by complicated algorithms and cryptographic keys, making it nearly impossible to tamper with or fake transactions.

End-to-End Encryption: Email, instant messages, and video chats are all examples of two-way communications protected by end-to-end encryption. Even if a message is encrypted, this guarantees that only the intended recipients can decode it. End-to-end encryption is frequently employed in messaging apps like WhatsApp and Signal, offering users high protection and anonymity.

RSA Encryption Algorithm

RSA encryption algorithm is a type of public-key encryption algorithm. To better understand RSA, lets first understand what is public-key encryption algorithm.

Public key encryption algorithm:

Public Key encryption algorithm is also called the Asymmetric algorithm. Asymmetric algorithms are those algorithms in which sender and receiver use different keys for encryption and decryption. Each sender is assigned a pair of keys:

• Public key
• Private key

The Public key is used for encryption, and the Private Key is used for decryption. Decryption cannot be done using a public key. The two keys are linked, but the private key cannot be derived from the public key. The public key is well known, but the private key is secret and it is known only to the user who owns the key. It means that everybody can send a message to the user using user's public key. But only the user can decrypt the message using his private key.

The Public key algorithm operates in the following manner:

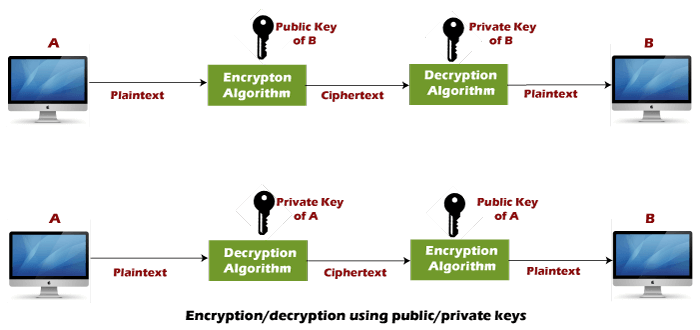
• The data to be sent is encrypted by sender A using the public key of the intended receiver
• B decrypts the received ciphertext using its private key, which is known only to B. B replies to A encrypting its message using A's public key.
• A decrypts the received ciphertext using its private key, which is known only to him.

RSA encryption algorithm:

RSA is the most common public-key algorithm, named after its inventors Rivest, Shamir, and Adelman (RSA).

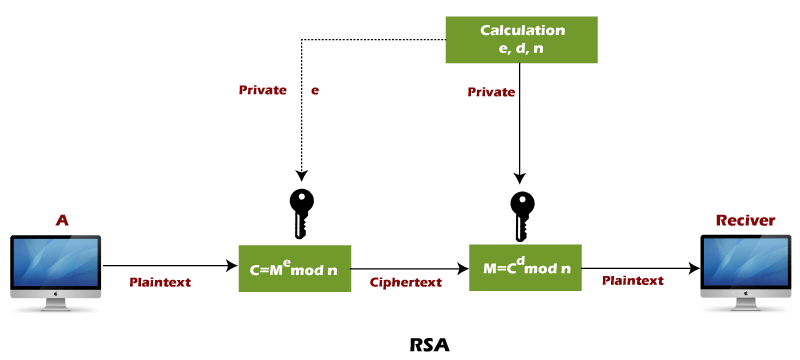
RSA algorithm uses the following procedure to generate public and private keys:

• Select two large prime numbers, p and q.
• Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.
• Choose a number e less than n, such that n is relatively prime to (p - 1) x (q -1). It means that e and (p - 1) x (q - 1) have no common factor except 1. Choose "e" such that 1<e < φ (n), e is prime to φ (n),
  gcd (e,d(n)) =1
• If n = p x q, then the public key is <e, n>. A plaintext message m is encrypted using public key <e, n>. To find ciphertext from the plain text following formula is used to get ciphertext C.
  C = m^e mod n
  Here, m must be less than n. A larger message (>n) is treated as a concatenation of messages, each of which is encrypted separately.
• To determine the private key, we use the following formula to calculate the d such that:
  D_e mod {(p - 1) x (q - 1)} = 1
  Or
  D_e mod φ (n) = 1
• The private key is <d, n>. A ciphertext message c is decrypted using private key <d, n>. To calculate plain text m from the ciphertext c following formula is used to get plain text m.
  m = c^d mod n

Example of RSA encryption algorithm:

Example 1:

This example shows how we can encrypt plaintext 9 using the RSA public-key encryption algorithm. This example uses prime numbers 7 and 11 to generate the public and private keys.

Explanation:

Step 1: Select two large prime numbers, p, and q.

p = 7

q = 11

Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.

First, we calculate

n = p x q

n = 7 x 11

n = 77

Step 3: Choose a number e less that n, such that n is relatively prime to (p - 1) x (q -1). It means that e and (p - 1) x (q - 1) have no common factor except 1. Choose "e" such that 1<e < φ (n), e is prime to φ (n), gcd (e, d (n)) =1.

Second, we calculate

φ (n) = (p - 1) x (q-1)

φ (n) = (7 - 1) x (11 - 1)

φ (n) = 6 x 10

φ (n) = 60

Let us now choose relative prime e of 60 as 7.

Thus the public key is <e, n> = (7, 77)

Step 4: A plaintext message m is encrypted using public key <e, n>. To find ciphertext from the plain text following formula is used to get ciphertext C.

To find ciphertext from the plain text following formula is used to get ciphertext C.

C = m^e mod n

C = 9⁷ mod 77

C = 37

Step 5: The private key is <d, n>. To determine the private key, we use the following formula d such that:

D_e mod {(p - 1) x (q - 1)} = 1

7d mod 60 = 1, which gives d = 43

The private key is <d, n> = (43, 77)

Step 6: A ciphertext message c is decrypted using private key <d, n>. To calculate plain text m from the ciphertext c following formula is used to get plain text m.

m = c^d mod n

m = 37⁴³ mod 77

m = 9

In this example, Plain text = 9 and the ciphertext = 37

Example 2:

In an RSA cryptosystem, a particular A uses two prime numbers, 13 and 17, to generate the public and private keys. If the public of A is 35. Then the private key of A is ……………?.

Explanation:

Step 1: in the first step, select two large prime numbers, p and q.

p = 13

q = 17

Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.

First, we calculate

n = p x q

n = 13 x 17

n = 221

Step 3: Choose a number e less that n, such that n is relatively prime to (p - 1) x (q -1). It means that e and (p - 1) x (q - 1) have no common factor except 1. Choose "e" such that 1<e < φ (n), e is prime to φ (n), gcd (e, d (n)) =1.

Second, we calculate

φ (n) = (p - 1) x (q-1)

φ (n) = (13 - 1) x (17 - 1)

φ (n) = 12 x 16

φ (n) = 192

g.c.d (35, 192) = 1

Step 3: To determine the private key, we use the following formula to calculate the d such that:

Calculate       d = d_e mod φ (n) = 1

d = d x 35 mod 192 = 1

d = (1 + k.φ (n))/e           [let k =0, 1, 2, 3………………]

Put k = 0

d = (1 + 0 x 192)/35

d = 1/35

Put k = 1

d = (1 + 1 x 192)/35

d = 193/35

Put k = 2

d = (1 + 2 x 192)/35

d = 385/35

d = 11

The private key is <d, n> = (11, 221)

Hence, private key i.e. d = 11

Example 3:

A RSA cryptosystem uses two prime numbers 3 and 13 to generate the public key= 3 and the private key = 7. What is the value of cipher text for a plain text?

Explanation:

Step 1: In the first step, select two large prime numbers, p and q.

p = 3

q = 13

Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.

First, we calculate

n = p x q

n = 3 x 13

n = 39

Step 3: If n = p x q, then the public key is <e, n>. A plaintext message m is encrypted using public key <e, n>. Thus the public key is <e, n> = (3, 39).

To find ciphertext from the plain text following formula is used to get ciphertext C.

C = m^e mod n

C = 5³ mod 39

C = 125 mod 39

C = 8

Hence, the ciphertext generated from plain text, C = 8.

Example 4:

A RSA cryptosystem uses two prime numbers, 3 and 11, to generate private key = 7. What is the value of ciphertext for a plain text 5 using the RSA public-key encryption algorithm?

Explanation:

Step 1: in the first step, select two large prime numbers, p and q.

p = 3

q = 11

Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.

First, we calculate

n = p x q

n = 3 x 11

n = 33

Step 3: Choose a number e less that n, such that n is relatively prime to (p - 1) x (q -1). It means that e and (p - 1) x (q - 1) have no common factor except 1. Choose "e" such that 1< e < φ (n), e is prime to φ (n), gcd (e, d (n)) =1.

Second, we calculate

φ (n) = (p - 1) x (q-1)

φ (n) = (3 - 1) x (11 - 1)

φ (n) = 2 x 10

φ (n) = 20

Step 4: To determine the public key, we use the following formula to calculate the d such that:

Calculate e x d = 1 mod φ (n)

e x 7 = 1 mod 20

e x 7 = 1 mod 20

e = (1 + k. φ (n))/ d              [let k =0, 1, 2, 3………………]

Put k = 0

e = (1 + 0 x 20) / 7

e = 1/7

Put k = 1

e = (1 + 1 x 20) / 7

e = 21/7

e = 3

The public key is <e, n> = (3, 33)

Hence, public key i.e. e = 3