Here knapsack is like a container or a bag. Suppose we have given some items which have some weights or profits. We have to put some items in the knapsack in such a way total value produces a maximum profit.
For example, the weight of the container is 20 kg. We have to select the items in such a way that the sum of the weight of items should be either smaller than or equal to the weight of the container, and the profit should be maximum.
There are two types of knapsack problems:
- 0/1 knapsack problem
- Fractional knapsack problem
What is the 0/1 knapsack problem?
The 0/1 knapsack problem means that the items are either completely or no items are filled in a knapsack. For example, we have two items having weights 2kg and 3kg, respectively. If we pick the 2kg item then we cannot pick 1kg item from the 2kg item (item is not divisible); we have to pick the 2kg item completely. This is a 0/1 knapsack problem in which either we pick the item completely or we will pick that item. The 0/1 knapsack problem is solved by the dynamic programming.
What is the fractional knapsack problem?
The fractional knapsack problem means that we can divide the item. For example, we have an item of 3 kg then we can pick the item of 2 kg and leave the item of 1 kg. The fractional knapsack problem is solved by the Greedy approach.
Algorithm of 0/1 Knapsack Problem
1. for w = 0, W 2. do V [0,w] ← 0 3. for i=0, n 4. do V [i, 0] ← 0 5. for w = 0, W 6. do if (wi≤ w & vi + V [i-1, w - wi]> V [i -1,W]) 7. then V [i, W] ← vi + V [i - 1, w - wi] 8. else V [i, W] ← V [i - 1, w]
Example of 0/1 knapsack problem.
Consider the problem having weights and profits are:
Weights: {3, 4, 6, 5}
Profits: {2, 3, 1, 4}
The weight of the knapsack is 8 kg
The number of items is 4
The above problem can be solved by using the following method:
xi = {1, 0, 0, 1}
= {0, 0, 0, 1}
= {0, 1, 0, 1}
The above are the possible combinations. 1 denotes that the item is completely picked and 0 means that no item is picked. Since there are 4 items so possible combinations will be:
24 = 16; So. There are 16 possible combinations that can be made by using the above problem. Once all the combinations are made, we have to select the combination that provides the maximum profit.
Another approach to solve the problem is dynamic programming approach. In dynamic programming approach, the complicated problem is divided into sub-problems, then we find the solution of a sub-problem and the solution of the sub-problem will be used to find the solution of a complex problem.
How this problem can be solved by using the Dynamic programming approach?
First,
we create a matrix shown as below:
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
0 | |||||||||
1 | |||||||||
2 | |||||||||
3 | |||||||||
4 |
In the above matrix, columns represent the weight, i.e., 8. The rows represent the profits and weights of items. Here we have not taken the weight 8 directly, problem is divided into sub-problems, i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8. The solution of the sub-problems would be saved in the cells and answer to the problem would be stored in the final cell. First, we write the weights in the ascending order and profits according to their weights shown as below:
wi = {3, 4, 5, 6}
pi = {2, 3, 4, 1}
The first row and the first column would be 0 as there is no item for w=0
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
| |||||||
|
2 |
0 |
| |||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
w1 = 3; Since we have only one item in the set having weight 3, but the capacity of the knapsack is 1. We cannot fill the item of 3kg in the knapsack of capacity 1 kg so add 0 at M[1][1] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
| ||||||
|
2 |
0 |
| |||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i = 1, W = 2
w1 = 3; Since we have only one item in the set having weight 3, but the capacity of the knapsack is 2. We cannot fill the item of 3kg in the knapsack of capacity 2 kg so add 0 at M[1][2] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
| |||||
|
2 |
0 |
| |||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i=1, W=3
w1 = 3; Since we have only one item in the set having weight equal to 3, and weight of the knapsack is also 3; therefore, we can fill the knapsack with an item of weight equal to 3. We put profit corresponding to the weight 3, i.e., 2 at M[1][3] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
| ||||
|
2 |
0 |
| |||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i=1, W = 4
W1 = 3; Since we have only one item in the set having weight equal to 3, and weight of the knapsack is 4; therefore, we can fill the knapsack with an item of weight equal to 3. We put profit corresponding to the weight 3, i.e., 2 at M[1][4] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
| |||
|
2 |
0 |
| |||||||
|
3 |
0 |
||||||||
|
4 |
0 |
|
When i=1, W = 5
W1 = 3; Since we have only one item in the set having weight equal to 3, and weight of the knapsack is 5; therefore, we can fill the knapsack with an item of weight equal to 3. We put profit corresponding to the weight 3, i.e., 2 at M[1][5] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
| ||
|
2 |
0 |
| |||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i =1, W=6
W1 = 3; Since we have only one item in the set having weight equal to 3, and weight of the knapsack is 6; therefore, we can fill the knapsack with an item of weight equal to 3. We put profit corresponding to the weight 3, i.e., 2 at M[1][6] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
| |
|
2 |
0 |
| |||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i=1, W = 7
W1 = 3; Since we have only one item in the set having weight equal to 3, and weight of the knapsack is 7; therefore, we can fill the knapsack with an item of weight equal to 3. We put profit corresponding to the weight 3, i.e., 2 at M[1][7] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
|
|
2 |
0 |
| |||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i =1, W =8
W1 = 3; Since we have only one item in the set having weight equal to 3, and weight of the knapsack is 8; therefore, we can fill the knapsack with an item of weight equal to 3. We put profit corresponding to the weight 3, i.e., 2 at M[1][8] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
| |||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
Now the value of 'i' gets incremented, and becomes 2.
When i =2, W = 1
The weight corresponding to the value 2 is 4, i.e., w2 = 4. Since we have only one item in the set having weight equal to 4, and the weight of the knapsack is 1. We cannot put the item of weight 4 in a knapsack, so we add 0 at M[2][1] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
| ||||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i =2, W = 2
The weight corresponding to the value 2 is 4, i.e., w2 = 4. Since we have only one item in the set having weight equal to 4, and the weight of the knapsack is 2. We cannot put the item of weight 4 in a knapsack, so we add 0 at M[2][2] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
| |||||
|
3 |
0 |
| |||||||
|
4 |
0 |
When i =2, W = 3
The weight corresponding to the value 2 is 4, i.e., w2 = 4. Since we have two items in the set having weights 3 and 4, and the weight of the knapsack is 3. We can put the item of weight 3 in a knapsack, so we add 2 at M[2][3] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
| ||||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i =2, W = 4
The weight corresponding to the value 2 is 4, i.e., w2 = 4. Since we have two items in the set having weights 3 and 4, and the weight of the knapsack is 4. We can put item of weight 4 in a knapsack as the profit corresponding to weight 4 is more than the item having weight 3, so we add 3 at M[2][4] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
| |||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i = 2, W = 5
The weight corresponding to the value 2 is 4, i.e., w2 = 4. Since we have two items in the set having weights 3 and 4, and the weight of the knapsack is 5. We can put item of weight 4 in a knapsack and the profit corresponding to weight is 3, so we add 3 at M[2][5] shown as below:.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
| ||
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i = 2, W = 6
The weight corresponding to the value 2 is 4, i.e., w2 = 4. Since we have two items in the set having weights 3 and 4, and the weight of the knapsack is 6. We can put item of weight 4 in a knapsack and the profit corresponding to weight is 3, so we add 3 at M[2][6] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
| |
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i = 2, W = 7
The weight corresponding to the value 2 is 4, i.e., w2 = 4. Since we have two items in the set having weights 3 and 4, and the weight of the knapsack is 7. We can put item of weight 4 and 3 in a knapsack and the profits corresponding to weights are 2 and 3; therefore, the total profit is 5, so we add 5 at M[2][7] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
|
|
3 |
0 |
| |||||||
|
4 |
0 |
|
When i = 2, W = 8
The weight corresponding to the value 2 is 4, i.e., w2 = 4. Since we have two items in the set having weights 3 and 4, and the weight of the knapsack is 7. We can put item of weight 4 and 3 in a knapsack and the profits corresponding to weights are 2 and 3; therefore, the total profit is 5, so we add 5 at M[2][7] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
| |||||||
|
4 |
0 |
|
Now the value of 'i' gets incremented, and becomes 3.
When i = 3, W = 1
The weight corresponding to the value 3 is 5, i.e., w3 = 5. Since we have three items in the set having weights 3, 4, and 5, and the weight of the knapsack is 1. We cannot put neither of the items in a knapsack, so we add 0 at M[3][1] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
| ||||||
|
4 |
0 |
When i = 3, W = 2
The weight corresponding to the value 3 is 5, i.e., w3 = 5. Since we have three items in the set having weight 3, 4, and 5, and the weight of the knapsack is 1. We cannot put neither of the items in a knapsack, so we add 0 at M[3][2] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
| |||||
|
4 |
0 |
|
When i = 3, W = 3
The weight corresponding to the value 3 is 5, i.e., w3 = 5. Since we have three items in the set of weight 3, 4, and 5 respectively and weight of the knapsack is 3. The item with a weight 3 can be put in the knapsack and the profit corresponding to the item is 2, so we add 2 at M[3][3] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
| ||||
|
4 |
0 |
|
When i = 3, W = 4
The weight corresponding to the value 3 is 5, i.e., w3 = 5. Since we have three items in the set of weight 3, 4, and 5 respectively, and weight of the knapsack is 4. We can keep the item of either weight 3 or 4; the profit (3) corresponding to the weight 4 is more than the profit corresponding to the weight 3 so we add 3 at M[3][4] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
| |||
|
4 |
0 |
|
When i = 3, W = 5
The weight corresponding to the value 3 is 5, i.e., w3 = 5. Since we have three items in the set of weight 3, 4, and 5 respectively, and weight of the knapsack is 5. We can keep the item of either weight 3, 4 or 5; the profit (3) corresponding to the weight 4 is more than the profits corresponding to the weight 3 and 5 so we add 3 at M[3][5] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
| ||
|
4 |
0 |
|
When i =3, W = 6
The weight corresponding to the value 3 is 5, i.e., w3 = 5. Since we have three items in the set of weight 3, 4, and 5 respectively, and weight of the knapsack is 6. We can keep the item of either weight 3, 4 or 5; the profit (3) corresponding to the weight 4 is more than the profits corresponding to the weight 3 and 5 so we add 3 at M[3][6] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
| |
|
4 |
0 |
|
When i =3, W = 7
The weight corresponding to the value 3 is 5, i.e., w3 = 5. Since we have three items in the set of weight 3, 4, and 5 respectively, and weight of the knapsack is 7. In this case, we can keep both the items of weight 3 and 4, the sum of the profit would be equal to (2 + 3), i.e., 5, so we add 5 at M[3][7] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
|
|
4 |
0 |
|
When i = 3, W = 8
The weight corresponding to the value 3 is 5, i.e., w3 = 5. Since we have three items in the set of weight 3, 4, and 5 respectively, and the weight of the knapsack is 8. In this case, we can keep both the items of weight 3 and 4, the sum of the profit would be equal to (2 + 3), i.e., 5, so we add 5 at M[3][8] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
|
When i = 4, W = 1
The weight corresponding to the value 4 is 6, i.e., w4 = 6. Since we have four items in the set of weights 3, 4, 5, and 6 respectively, and the weight of the knapsack is 1. The weight of all the items is more than the weight of the knapsack, so we cannot add any item in the knapsack; Therefore, we add 0 at M[4][1] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
|
When i = 4, W = 2
The weight corresponding to the value 4 is 6, i.e., w4 = 6. Since we have four items in the set of weights 3, 4, 5, and 6 respectively, and the weight of the knapsack is 2. The weight of all the items is more than the weight of the knapsack, so we cannot add any item in the knapsack; Therefore, we add 0 at M[4][2] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
|
The weight corresponding to the value 4 is 6, i.e., w4 = 6. Since we have four items in the set of weights 3, 4, 5, and 6 respectively, and the weight of the knapsack is 3. The item with a weight 3 can be put in the knapsack and the profit corresponding to the weight 4 is 2, so we will add 2 at M[4][3] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
|
When i = 4, W = 4
The weight corresponding to the value 4 is 6, i.e., w4 = 6. Since we have four items in the set of weights 3, 4, 5, and 6 respectively, and the weight of the knapsack is 4. The item with a weight 4 can be put in the knapsack and the profit corresponding to the weight 4 is 3, so we will add 3 at M[4][4] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
3 |
|
When i = 4, W = 5
The weight corresponding to the value 4 is 6, i.e., w4 = 6. Since we have four items in the set of weights 3, 4, 5, and 6 respectively, and the weight of the knapsack is 5. The item with a weight 4 can be put in the knapsack and the profit corresponding to the weight 4 is 3, so we will add 3 at M[4][5] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
3 |
4 |
|
When i = 4, W = 6
The weight corresponding to the value 4 is 6, i.e., w4 = 6. Since we have four items in the set of weights 3, 4, 5, and 6 respectively, and the weight of the knapsack is 6. In this case, we can put the items in the knapsack either of weight 3, 4, 5 or 6 but the profit, i.e., 4 corresponding to the weight 6 is highest among all the items; therefore, we add 4 at M[4][6] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
|
|
The weight corresponding to the value 4 is 6, i.e., w4 = 6. Since we have four items in the set of weights 3, 4, 5, and 6 respectively, and the weight of the knapsack is 7. Here, if we add two items of weights 3 and 4 then it will produce the maximum profit, i.e., (2 + 3) equals to 5, so we add 5 at M[4][7] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
3 |
3 |
4 |
5 |
|
When i = 4, W = 8
The weight corresponding to the value 4 is 6, i.e., w4 = 6. Since we have four items in the set of weights 3, 4, 5, and 6 respectively, and the weight of the knapsack is 8. Here, if we add two items of weights 3 and 4 then it will produce the maximum profit, i.e., (2 + 3) equals to 5, so we add 5 at M[4][8] shown as below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
As we can observe in the above table that 5 is the maximum profit among all the entries. The pointer points to the last row and the last column having 5 value. Now we will compare 5 value with the previous row; if the previous row, i.e., i = 3 contains the same value 5 then the pointer will shift upwards. Since the previous row contains the value 5 so the pointer will be shifted upwards as shown in the below table:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
Again, we will compare the value 5 from the above row, i.e., i = 2. Since the above row contains the value 5 so the pointer will again be shifted upwards as shown in the below table:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
Again, we will compare the value 5 from the above row, i.e., i = 1. Since the above row does not contain the same value so we will consider the row i=1, and the weight corresponding to the row is 4. Therefore, we have selected the weight 4 and we have rejected the weights 5 and 6 shown below:
x = { 1, 0, 0}
The profit corresponding to the weight is 3. Therefore, the remaining profit is (5 - 3) equals to 2. Now we will compare this value 2 with the row i = 2. Since the row (i = 1) contains the value 2; therefore, the pointer shifted upwards shown below:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
0 |
0 |
0 |
2 |
3 |
3 |
3 |
5 |
5 |
|
3 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
|
4 |
0 |
0 |
0 |
2 |
3 |
4 |
4 |
5 |
6 |
Again we compare the value 2 with a above row, i.e., i = 1. Since the row i =0 does not contain the value 2, so row i = 1 will be selected and the weight corresponding to the i = 1 is 3 shown below:
X = {1, 0, 0, 1}
The profit corresponding to the weight is 2. Therefore, the remaining profit is 0. We compare 0 value with the above row. Since the above row contains a 0 value but the profit corresponding to this row is 0. In this problem, two weights are selected, i.e., 3 and 4 to maximize the profit.
Example: The maximum weight the knapsack can hold is W is 11. There are five items to choose from. Their weights and values are presented in the following table:
The [i, j] entry here will be V [i, j], the best value obtainable using the first "i" rows of items if the maximum capacity were j. We begin by initialization and first row.
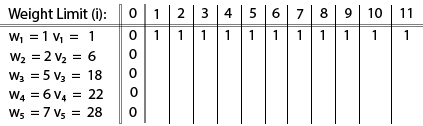
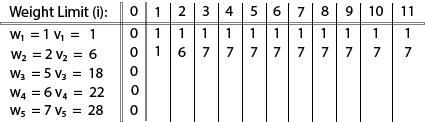
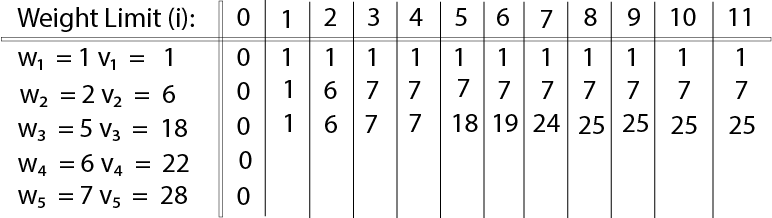
The value of V [3, 7] was computed as follows:
V [3, 7] = max {V [3 - 1, 7], v3 + V [3 - 1, 7 - w3]
= max {V [2, 7], 18 + V [2, 7 - 5]}
= max {7, 18 + 6}
= 24
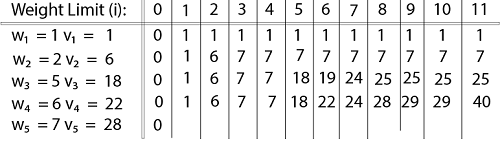
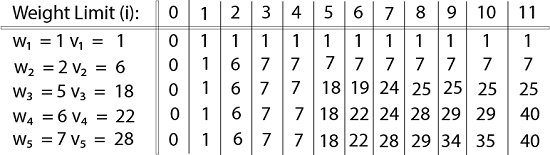
Finally, the output is:




No comments:
Post a Comment