Floyd-Warshall Algorithm

Let the vertices of G be V = {1, 2........n} and consider a subset {1, 2........k} of vertices for some k. For any pair of vertices i, j ∈ V, considered all paths from i to j whose intermediate vertices are all drawn from {1, 2.......k}, and let p be a minimum weight path from amongst them. The Floyd-Warshall algorithm exploits a link between path p and shortest paths from i to j with all intermediate vertices in the set {1, 2.......k-1}. The link depends on whether or not k is an intermediate vertex of path p.

If k is not an intermediate vertex of path p, then all intermediate vertices of path p are in the set {1, 2........k-1}. Thus, the shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2.......k-1} is also the shortest path i to j with all intermediate vertices in the set {1, 2.......k}.

If k is an intermediate vertex of path p, then we break p down into i → k → j.

Let d_ij^(k) be the weight of the shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2.......k}.

FLOYD - WARSHALL (W)

 1. n ← rows [W].
 2. D0 ← W
 3. for k ← 1 to n
 4.     do for i ← 1 to n     
 5.         do for j ← 1 to n     
 6.             do dij(k) ← min (dij(k-1),dik(k-1)+dkj(k-1) )
 7. return D(n)

The strategy adopted by the Floyd-Warshall algorithm is Dynamic Programming. The running time of the Floyd-Warshall algorithm is determined by the triply nested for loops of lines 3-6. Each execution of line 6 takes O (1) time. The algorithm thus runs in time θ(n³ ).

Principle of optimality :

If k is the node on the shortest path from i to j, then the path from i to k and k to j, must also be shortest.

In the following figure, the optimal path from i to j is either p or summation of p₁ and p₂.

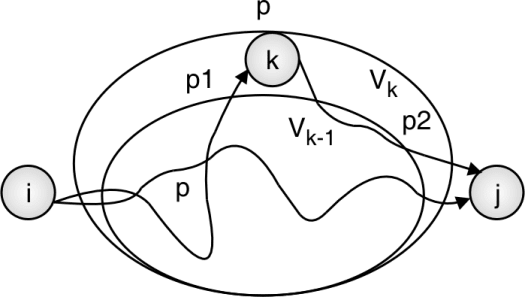
While considering k^th vertex as intermediate vertex, there are two possibilities :

• If k is not part of shortest path from i to j, we keep the distance D[i, j] as it is.
• If k is part of shortest path from i to j, update distance D[i, j] as
  D[i, k] + D[k, j].

Optimal sub structure of the problem is given as :

D^k [i, j] = min{ D^{k – 1} [i, j], D^{k – 1} [i, k] + D^{k – 1} [k, j] }

D^k = Distance matrix after k^th iteration

Example: Shortcut Process

Example:

Step (i) When k = 0

Step (ii) When k =1

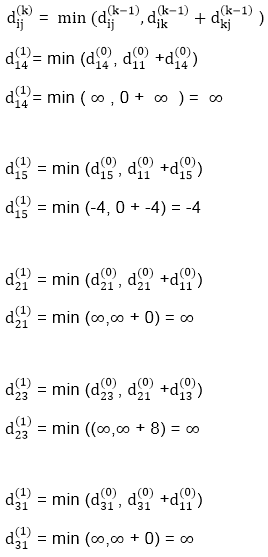
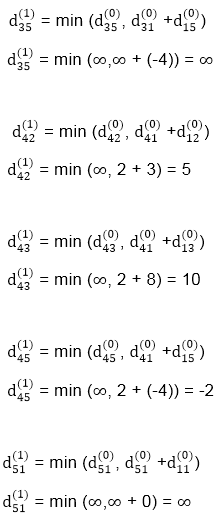
Step (iii) When k = 2

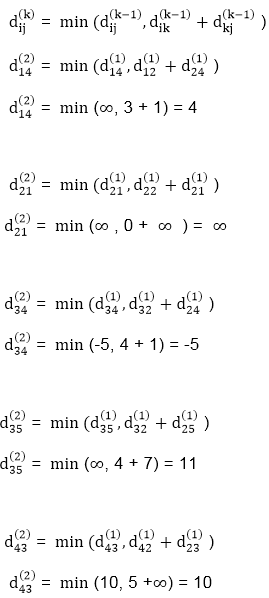
Step (iv) When k = 3

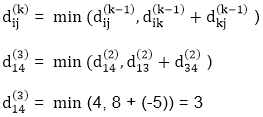
Step (v) When k = 4

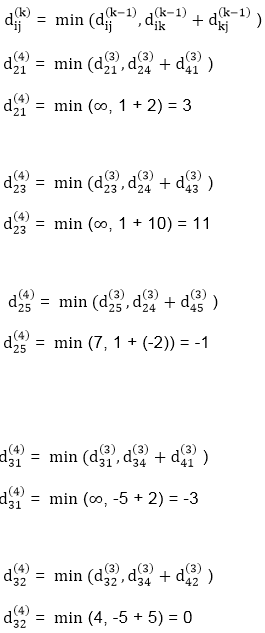
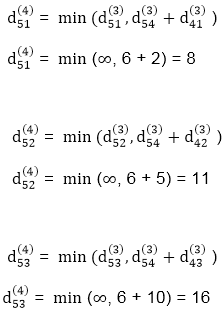
Step (vi) When k = 5

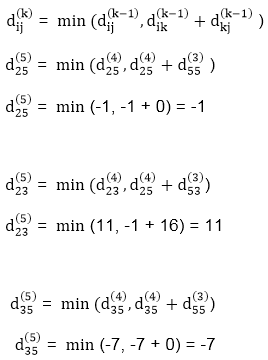
Problem: Apply Floyd’s method to find the shortest path for the below-mentioned all pairs.

Solution:

Optimal substructure formula for Floyd’s algorithm,                                

D^k [i, j] = min { D^{k – 1} [i, j], D^{k – 1} [i, k] + D^{k – 1} [k, j] }

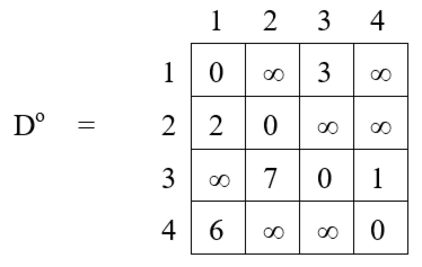
Iteration 1 : k = 1 :

D¹[1, 2] = min { D^o [1, 2], D^o [1, 1] + D^o [1, 2] }

= min {∞, 0 + ∞} 

=  ∞

D¹[1, 3] = min { D^o [1, 3], D^o [1, 1] + D^o [1, 3] }

= min {3, 0 + 3} 

= 3

D¹[1, 4] = min { D^o [1, 4], D^o [1, 1] + D^o [1, 4] }

= min {∞, 0 + ∞} 

=  ∞

D¹[2, 1] = min { D^o [2, 1], D^o [2, 1] + D^o [1, 1] }

= min {2, 2 + 0} 

= 2

D¹[2, 3] = min { D^o [2, 3], D^o [2, 1] + D^o [1, 3] }

= min {∞, 2 + 3} 

= 5

D¹[2, 4] = min { D^o [2, 4], D^o [2, 1] + D^o [1, 4] }

= min {∞, 2 + ∞} 

= ∞

D¹[3, 1] = min { D^o [3, 1], D^o [3, 1] + D^o [1, 1] }

= min {∞, 0 + ∞} 

= ∞

D¹[3, 2] = min { D^o [3, 2], D^o [3, 1] + D^o [1, 2] }

= min {7, ∞ + ∞} 

= 7

D¹[3, 4] = min { D^o [3, 4], D^o [3, 1] + D^o [1, 4] }

= min {1, ∞ + ∞} 

= 1

D¹[4, 1] = min { D^o [4, 1], D^o [4, 1] + D^o [1, 1] }

= min {6, 6 + 0} 

= 6

D¹[4, 2] = min { D^o [4, 2], D^o [4, 1] + D^o [1, 2] }

= min {∞, 6 + ∞} 

= ∞

D¹[4, 3] = min { D^o [4, 3], D^o [4, 1] + D^o [1, 3] }

= min {∞, 6 + 3} 

= 9

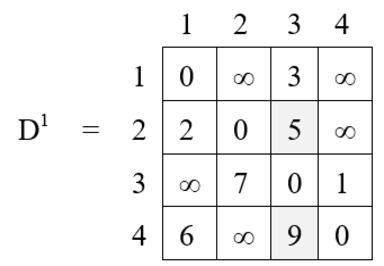
Note : Path distance for highlighted cell is improvement over original matrix.

Iteration 2 (k = 2) :

D²[1, 2] = D¹ [1, 2]  =  ∞

D²[1, 3] = min { D¹ [1, 3], D¹ [1, 2] + D¹ [2, 3] }

= min {3, ∞ + 5} 

= 3

D²[1, 4] = min { D¹ [1, 4], D¹ [1, 2] + D¹ [2, 4] }

= min {∞, ∞ + ∞} 

= ∞

D²[2, 1] = D¹ [2, 1]  =  2

D²[2, 3] = D¹ [2, 3]  =  5

D²[2, 4] = D¹ [2, 4]  =  ∞

D²[3, 1] = min { D¹ [3, 1], D¹ [3, 2] + D¹ [2, 1] }

= min {∞, 7 + 2} 

= 9

D²[3, 2] = D¹ [3, 2]  =  7

D²[3, 4] = min { D¹ [3, 4], D¹ [3, 2] + D¹ [2, 4] }

= min {1, 7 + ∞} 

= 1

D²[4, 1] = min { D¹ [4, 1], D¹ [4, 2] + D¹ [2, 1] }

= min {6, ∞ + 2} 

= 6

D²[4, 2] = D¹ [4, 2]  =  ∞                                

D²[4, 3]  =  min { D¹ [4, 3], D¹ [4, 2] + D¹ [2, 3] }

= min {9, ∞ + 5} 

= 9

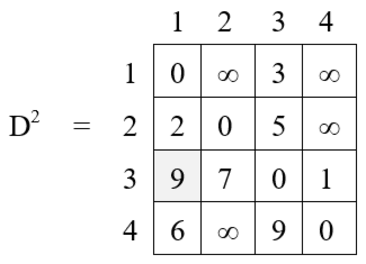
Iteration 3 (k = 3) :

D³[1, 2] = min { D² [1, 2], D² [1, 3] + D² [3, 2] }

= min {∞, 3 + 7} 

= 10

D³[1, 3] = D² [1, 3]  =  3

D³[1, 4] = min { D² [1, 4], D² [1, 3] + D² [3, 4] }

= min {∞, 3 + 1} 

= 4

D³[2, 1] = min { D² [2, 1], D² [2, 3] + D² [3, 1] }

= min {2, 5 + 9} 

= 2

D³[2, 3] = D² [2, 3]  =  5

D³[2, 4] = min { D² [2, 4], D² [2, 3] + D² [3, 4] }

= min {∞, 5 + 1} 

= 6

D³[3, 1] = D² [3, 1]  =  9

D³[3, 2] = D² [3, 2]  =  7

D³[3, 4] = D² [3, 4]  =  1

D³[4, 1] = min { D² [4, 1], D² [4, 3] + D² [3, 1] }

= min {6, 9 + 9} 

= 6

D³[4, 2] = min { D² [4, 1], D² [4, 3] + D² [3, 2] }

= min {∞, 9 + 7} 

= 16

D³[4, 3] = D² [4, 3]  =  9

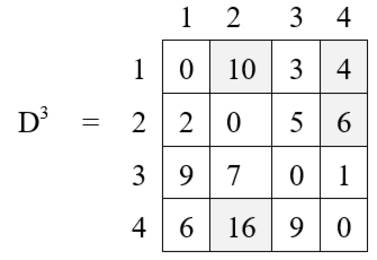
Iteration 4 (k = 4) :

D⁴[1, 2] = min { D³ [1, 2], D³ [1, 4] + D³ [4, 2] }

= min {10, 4 + 16} 

= 10

D⁴[1, 3] = min { D³ [1, 3], D³ [1, 4] + D³ [4, 1] }

= min {3, 4 + 9} 

= 3

D⁴[1, 4] = D³ [1, 4]  =  4

D⁴[2, 1] = min { D³ [2, 1], D³ [2, 4] + D³ [4, 1] }

= min {2, 6 + 6} 

= 2

D⁴[2, 3] = min { D³ [2, 3], D³ [2, 4] + D³ [4, 3] }

= min {5, 6 + 9} 

= 5

D⁴[2, 4] = D³ [2, 4]  =  6

D⁴[3, 1] = min { D³ [3, 1], D³ [3, 4] + D³ [4, 1] }

= min {9, 1 + 6} 

= 7

D⁴[3, 2] = min { D³ [3, 2], D³ [3, 4] + D³ [4, 2] }

= min {7, 1 + 16} 

= 7

D⁴[3, 4] = D³ [3, 4]  =  1

D⁴[4, 1] = D³ [4, 1]  =  6

D⁴[4, 2] = D³ [4, 2]  = 16

D⁴[4, 3] = D³ [4, 3]  =  9

Final distance matrix is,

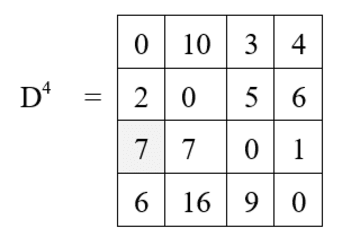
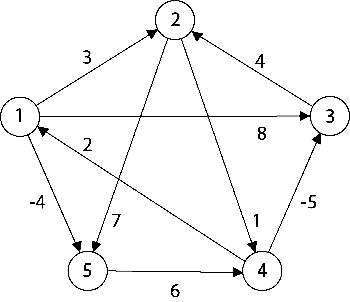
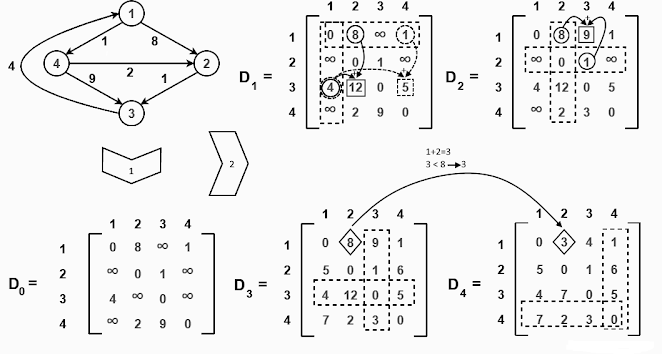
Problem: Obtain all pair shortest path using Floyd’s Algorithm for given weighted graph

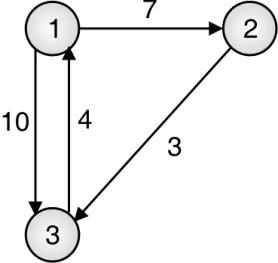
Solution:

Optimal substructure formula for Floyd’s algorithm,

D^k [i,j] = min{ D^{k – 1} [i, j], D^{k – 1} [i, k] + D^{k – 1} [k, j] }

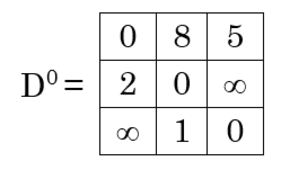
Iteration 1 (k = 1) :

D¹ [1, 2] = min {D⁰[1, 2], D⁰[1, 1] + D⁰[1, 2] }

= min {8, 0 + 8}

= 8

D¹[1, 3] = min {D⁰[1, 3], D⁰[1, 1] + D⁰[1, 3] }

= min {5, 0 + 5}

= 5

D¹[2, 1] = min {D⁰[2, 1], D⁰[2, 1] + D⁰[1, 1] }

= min {2, 2 + 0}

= 2

D¹[2, 3] = min {D⁰[2, 3], D⁰[2, 1] + D⁰[1, 3] }

= min {∞, 2 + 5}

= 7

D¹[3, 1] = min {D⁰[3, 1], D⁰[3, 1] + D⁰[1, 1] }

= min {∞, ∞ + 0}

= ∞

D¹[3, 2] = min {D⁰[3, 2], D⁰[3, 1] + D⁰[1, 2] }

= min {1, 1 + 8}

= 1

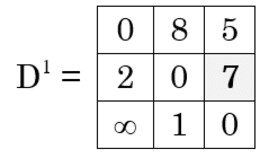
Iteration 2 (k = 2) :

D²[1, 2] = min {D¹[1, 2],  D¹[1, 2] + D¹[2, 2]}

= min {8, 8 + 0}

= 8

D²[1, 3] = min {D¹[1, 3], D¹[1, 2] +  D¹[2, 3] }

= min {5, 8 +7}

= 5

D²[2, 1] = min {D¹[2, 1], D¹[2, 2] + D¹[2, 1}

=  min {2, 0 + 2}

= 2

D²[2, 3] = min {D¹[2, 3], D¹[2, 2] + D¹[2, 3] }

=  min {7, 0 + 7}

= 7

D²[3, 1] = min {D¹[3, 1], D¹[3, 2] + D¹[2, 1] }

= min {∞, 1 + 2}

= 3

D²[3, 2] = min {D¹[3, 2], D¹[3, 2] + D¹[2, 2] }

= min {1, 1 + 0}

= 1

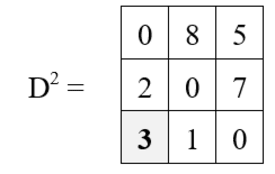
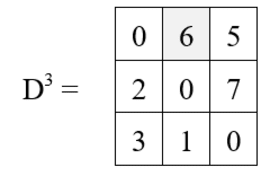
Iteration 3 (k = 3) :

D³[1, 2] = min {D²[1, 2],  D²[1, 3] + D²[3, 2]}

= min {8, 5 + 1}

= 6

D³[1, 3] = min {D²[1, 3], D²[1, 3] +  D²[3, 3] }

= min {5, 5 + 0}

= 5

D³[2, 1] = min {D²[2, 1], D²[2, 3] + D²[3, 1}

= min {2, 7 + 3}

= 2

D³[2, 3] = min {D²[2, 3], D²[2, 3] + D²[3, 3] }

= min {7, 7 + 0}

= 7

D³[3, 1] = min {D²[3, 1], D²[3, 3] + D²[3, 1] }

= min {3, 0 + 3}

= 3

D³[3, 2] = min {D²[3, 2], D²[3, 3] + D²[3, 2] }

= min {1, 0 + 1}

= 1