Multistage Graph problem

Resource Allocation Problem 

The resource allocation problem seeks to find an optimal allocation of a fixed amount of resources to activities so as to minimize the cost incurred by the allocation.

The amount of resources to be allocated to each activity is treated as a continuous or integer variable, depending on the cases. 

Resource Allocation or Resource Management is the scheduling of activities and the resources required by those activities while taking into consideration both the resource availability and the project time.

Resource allocation may be decided by using computer programs applied to a specific domain to automatically and dynamically distribute resources to applicants.

There are two types of dynamic resource allocation: 

Overflow

• Here all resources are pre-provisioned and ready
• We have a standby computer resource ready for on-demand access.

Tiering 

• Here all resources are pre-provisioned and ready
• We dynamically reprioritise an application’s access to the computer resources.

Using Multistage Graph 

Multistage Graph problem is defined as follow:

• Multistage graph G = (V, E, W) is a weighted directed graph in which vertices are partitioned into k ≥ 2 disjoint sub sets V = {V₁, V₂, …, V_k} such that if edge (u, v) is present in E then u ∈ V_i and v ∈ V_i+1, 1 ≤ i ≤ k. The goal of multistage graph problem is to find minimum cost path from source to destination vertex.
• The input to the algorithm is a k-stage graph, n vertices are indexed in increasing order of stages.
• The algorithm operates in the backward direction, i.e. it starts from the last vertex of the graph and proceeds in a backward direction to find minimum cost path.
• Minimum cost of vertex j ∈ V_i from vertex r ∈ V_i+1 is defined as,

Cost[j] = min{ c[j, r] + cost[r] }

         where, c[j, r] is the weight of edge <j, r> and cost[r] is the cost of moving from end vertex to vertex r.

• Algorithm for the multistage graph is described below :

Algorithm for Multistage Graph

Algorithm MULTI_STAGE(G, k, n, p)
// Description: Solve multi-stage problem using dynamic programming

// Input:
k: Number of stages in graph G = (V, E)
c[i, j]:Cost of edge (i, j)

// Output: p[1:k]:Minimum cost path

cost[n] ← 0
for j ← n – 1 to 1 do
    //Let r be a vertex such that (j, r) in E and c[j, r]+cost[r] is minimum
    cost[j] ← c[j, r] + cost[r]
    π[j] ← r
end

//Find minimum cost path
p[1] ← 1
p[k] ← n

for j ← 2 to k - 1 do
    p[j] ← π[p[j - 1]]
end

Complexity Analysis of Multistage Graph

If graph G has |E| edges, then cost computation time would be O(n + |E|). The complexity of tracing the minimum cost path would be O(k), k < n. Thus total time complexity of multistage graph using dynamic programming would be O(n + |E|).

Example: Find minimum path cost between vertex s and t for following multistage graph using dynamic programming.

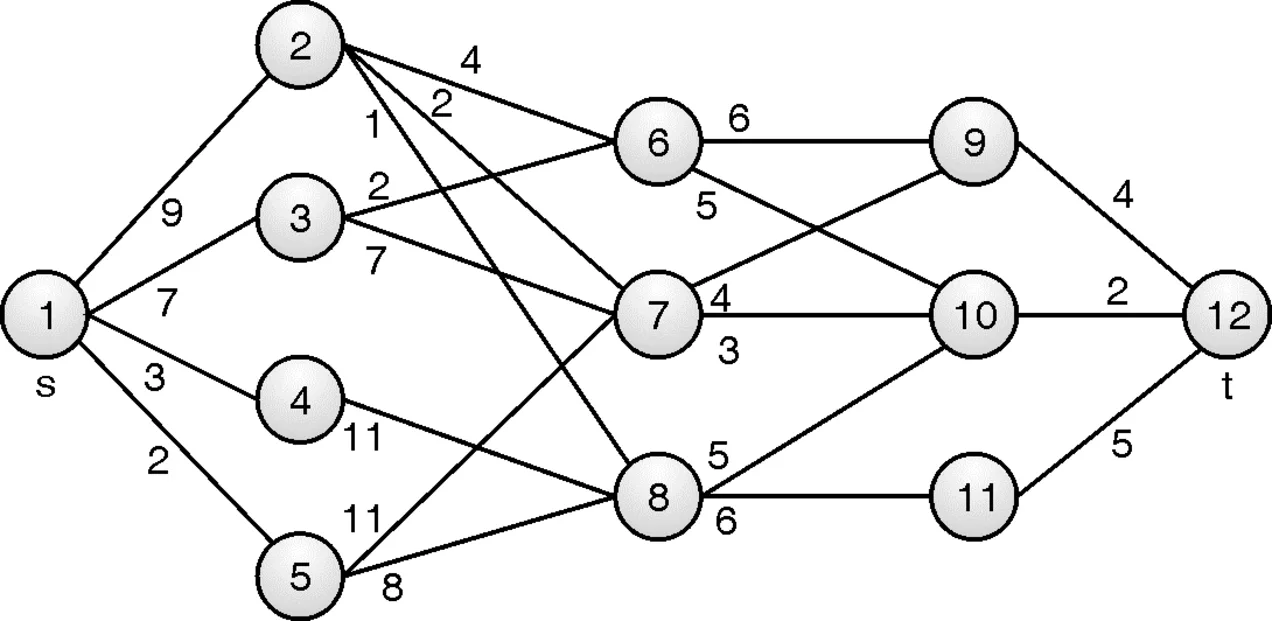
Solution:

Solution to multistage graph using dynamic programming is constructed as,

Cost[j] = min{c[j, r] + cost[r]}

Here, number of stages k = 5, number of vertices n = 12, source s = 1 and target t = 12

Initialization:

Cost[n] = 0 ⇒ Cost[12] = 0.

p[1] = s ⇒ p[1] = 1

p[k] = t ⇒ p[5] = 12.

r = t = 12.

Stage 4:

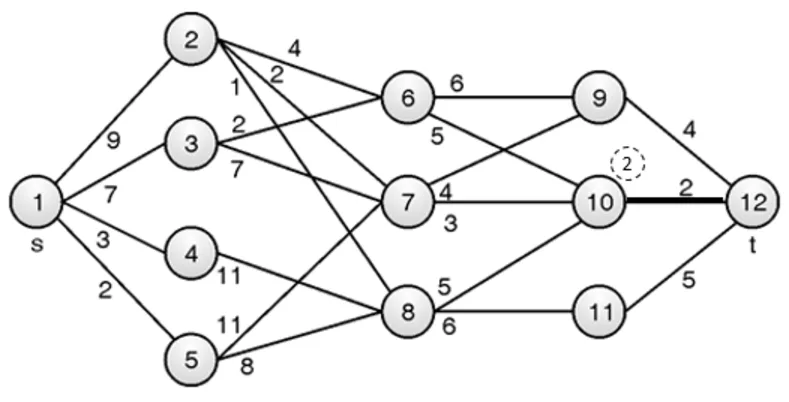
Stage 3:

Vertex 6 is connected to vertices 9 and 10:

Cost[6] = min{ c[6, 10] + Cost[10], c[6, 9] + Cost[9] }

= min{5 + 2, 6 + 4} = min{7, 10} = 7

p[6] = 10

Vertex 7 is connected to vertices 9 and 10:

Cost[7] = min{ c[7, 10] + Cost[10], c[7, 9] + Cost[9] }

= min{3 + 2, 4 + 4} = min{5, 8} = 5

p[7] = 10

Vertex 8 is connected to vertex 10 and 11:

Cost[8] = min{ c[8, 11] + Cost[11], c[8, 10] + Cost[10] }

= min{6 + 5, 5 + 2} = min{11, 7} = 7 p[8] = 10

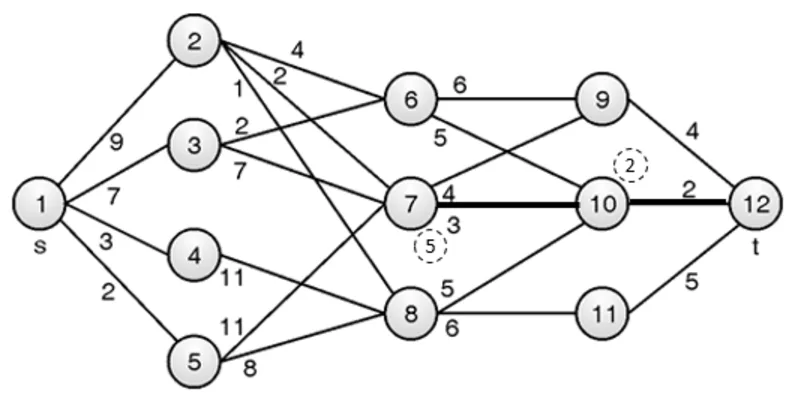
Stage 2:

Vertex 2 is connected to vertices6, 7 and 8:

Cost[2] = min{ c[2, 6] + Cost[6], c[2, 7] + Cost[7], c[2, 8] + Cost[8] }

= min{4 + 7, 2 + 5, 1 + 7} = min{11, 7, 8} = 7

p[2] = 7

Vertex 3 is connected to vertices 6and 7:

Cost[3] = min{ c[3, 6] + Cost[6], c[3, 7] + Cost[7] }

= min{2 + 7, 7 + 5} = min{9, 12} = 9

p[3] = 6

Vertex 4 is connected to vertex 8:

Cost[4] = c[4, 8] + Cost[8] = 11 + 7 = 18

p[4] = 8

Vertex 5 is connected to vertices 7 and 8:

Cost[5] = min{ c[5, 7] + Cost[7], c[5, 8] + Cost[8] }

= min{11 + 5, 8 + 7} = min{16, 15} = 15 p[5] = 8

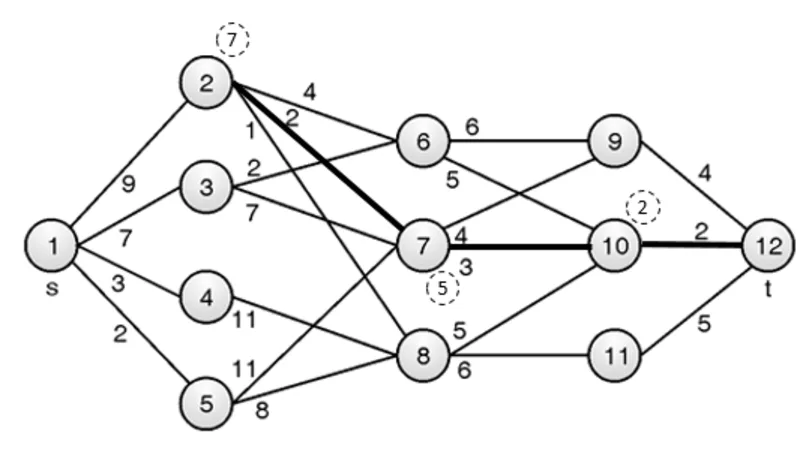
Stage 1:

Vertex 1 is connected to vertices 2, 3, 4 and 5:

Cost[1] = min{ c[1, 2] + Cost[2],  c[1, 3] + Cost[3], c[1, 4] + Cost[4], c[1, 5] + Cost[5]}

= min{ 9 + 7, 7 + 9, 3 + 18, 2 + 15 }

= min { 16, 16, 21, 17 } = 16 p[1] = 2

Trace the solution:

p[1] = 2

p[2] = 7

p[7] = 10

p[10] = 12

Minimum cost path is : 1 – 2 – 7 – 10 – 12

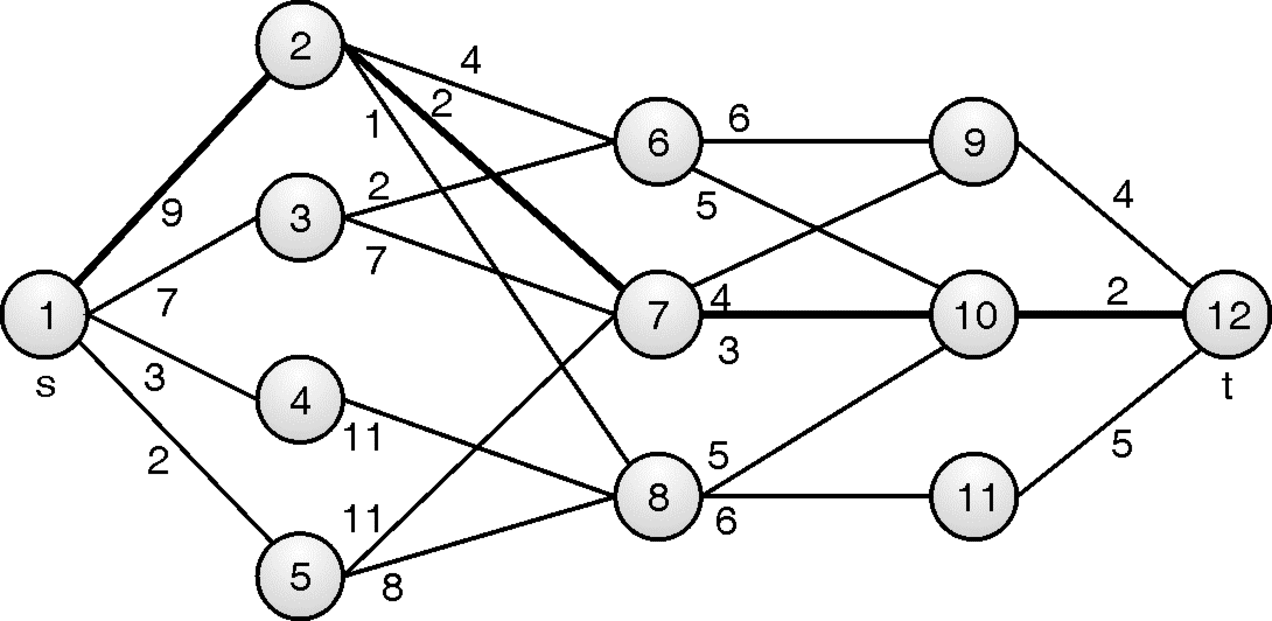
Cost of the path is : 9 + 2 + 3 + 2 = 16