Binary Heap

 A Binary Heap is a Binary Tree with following properties.

1) It’s a complete tree (All levels are completely filled except possibly the last level and the last level has all keys as left as possible). This property of Binary Heap makes them suitable to be stored in an array.

2) A Binary Heap is either Min Heap or Max Heap. In a Min Binary Heap, the key at root must be minimum among all keys present in Binary Heap. The same property must be recursively true for all nodes in Binary Tree. Max Binary Heap is similar to MinHeap.

Examples of Min Heap:

            10                      10
         /      \               /       \  
       20        100          15         30  
      /                      /  \        /  \
    30                     40    50    100   40

How is Binary Heap represented?
A Binary Heap is a Complete Binary Tree. A binary heap is typically represented as an array.

• The root element will be at Arr[0].
• Below table shows indexes of other nodes for the ith node, i.e., Arr[i]:
  

  Arr[(i-1)/2]	Returns the parent node
  Arr[(2*i)+1]	Returns the left child node
  Arr[(2*i)+2]	Returns the right child node

  The traversal method use to achieve Array representation is Level Order
  

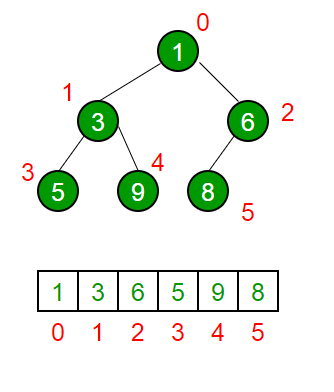
Array Representation Of Binary Heap

The complete binary tree that follows the properties of heap ordering is called binary heap.

Based on the ordering of binary heap, it can be of two types −

min Heap is the heap in which the value of node is greater than or equal to the value of its parent node. The root node of min heap is smallest.

max Heap is the heap in which the value of node is smaller than or equal to the value of its parent node. The root node of max heap is greatest.

The values of binary heap is typically represented as an array. The array representation of binary heap as −

• Index of the root element is 0.

• If i is the index of the node in the array. Then, the other nodes related to the node are index in the array as −

  • Left child : (2*i)+1

  • Right child : (2*i)+2

  • Parent child : (i-1)/2

Using the above rules of array representation of we can represent a heap in array −

1

4

7

8

9

11

12

Now, the types of heaps based on ordering can be discussed here

• Min Heap − The root node has the minimum value. The value of node is greater than value of parent node.

Example −

Array representation −

1

4

7

6

9

10

8

•  Max Heap − The root node has the maximum node. The value of node is smaller than the value of parent node.

Example −

Array representation −

11

8

9

6

4

5

1