Binary Search Algorithm

Binary search is the search technique that works efficiently on sorted lists. Hence, to search an element into some list using the binary search technique, we must ensure that the list is sorted.

Binary search follows the divide and conquer approach in which the list is divided into two halves, and the item is compared with the middle element of the list. If the match is found then, the location of the middle element is returned. Otherwise, we search into either of the halves depending upon the result produced through the match.

NOTE: Binary search can be implemented on sorted array elements. If the list elements are not arranged in a sorted manner, we have first to sort them.

Now, let's see the algorithm of Binary Search.

the working of the Binary search algorithm, let's take a sorted array. It will be easy to understand the working of Binary search with an example.

There are two methods to implement the binary search algorithm -

• Iterative method
• Recursive method

The recursive method of binary search follows the divide and conquer approach.

Let the elements of array are -

Let the element to search is, K = 56

We have to use the below formula to calculate the mid of the array -

mid = (beg + end)/2  

So, in the given array -

beg = 0

end = 8

mid = (0 + 8)/2 = 4. So, 4 is the mid of the array.

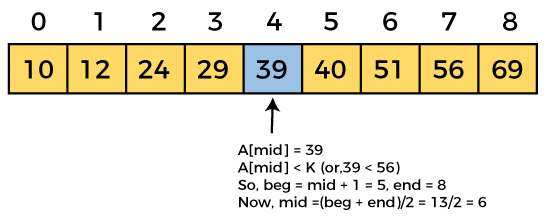
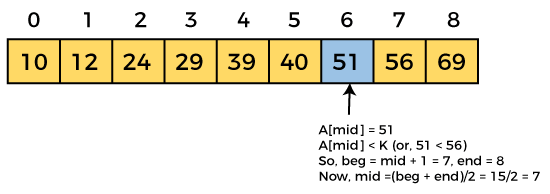
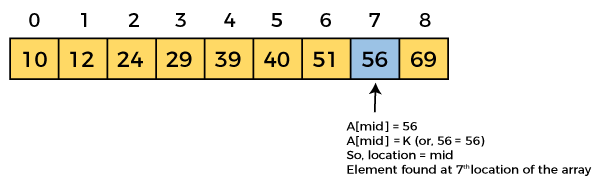
Now, the element to search is found. So algorithm will return the index of the element matched.

Binary Search complexity

Now, let's see the time complexity of Binary search in the best case, average case, and worst case. We will also see the space complexity of Binary search.

1. Time Complexity

Case	Time Complexity
Best Case	O(1)
Average Case	O(logn)
Worst Case	O(logn)

• Best Case Complexity - In Binary search, best case occurs when the element to search is found in first comparison, i.e., when the first middle element itself is the element to be searched. The best-case time complexity of Binary search is O(1).
• Average Case Complexity - The average case time complexity of Binary search is O(logn).
• Worst Case Complexity - In Binary search, the worst case occurs, when we have to keep reducing the search space till it has only one element. The worst-case time complexity of Binary search is O(logn).

2. Space Complexity

Space Complexity

O(1)

• The space complexity of binary search is O(1).

Implementation of Binary Search

Now, let's see the programs of Binary search in different programming languages.

Program: Write a program to implement Binary search in C language.

#include <stdio.h>  
int binarySearch(int a[], int beg, int end, int val)    
{    
    int mid;    
    if(end >= beg)     
    {        mid = (beg + end)/2;    
/* if the item to be searched is present at middle */  
        if(a[mid] == val)    
        {                 
            return mid+1;    
        }    
            /* if the item to be searched is smaller than middle, then it can only be in left subarray */  
        else if(a[mid] < val)     
        {  
            return binarySearch(a, mid+1, end, val);    
        }    
            /* if the item to be searched is greater than middle, then it can only be in right subarray */  
        else     
        {  
            return binarySearch(a, beg, mid-1, val);    
        }          
    }    
    return -1;     
}   
int main() {  
  int a[] = {11, 14, 25, 30, 40, 41, 52, 57, 70}; // given array  
  int val = 40; // value to be searched  
  int n = sizeof(a) / sizeof(a[0]); // size of array  
  int res = binarySearch(a, 0, n-1, val); // Store result  
  printf("The elements of the array are - ");  
  for (int i = 0; i < n; i++)  
  printf("%d ", a[i]);   
  printf("\nElement to be searched is - %d", val);  
  if (res == -1)  
  printf("\nElement is not present in the array");  
  else  
  printf("\nElement is present at %d position of array", res);  
  return 0;  
}

  

Output