What is a tree?
A tree is a kind of data structure that is used to represent the data in hierarchical form. It can be defined as a collection of objects or entities called as nodes that are linked together to simulate a hierarchy. Tree is a non-linear data structure as the data in a tree is not stored linearly or sequentially.
Now, let's start the topic, the Binary Search tree.
What is a Binary Search tree?
A binary search tree follows some order to arrange the elements. In a Binary search tree, the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node. This rule is applied recursively to the left and right subtrees of the root.
Let's understand the concept of Binary search tree with an example.
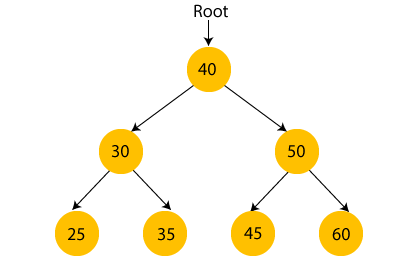
In the above figure, we can observe that the root node is 40, and all the nodes of the left subtree are smaller than the root node, and all the nodes of the right subtree are greater than the root node.
Similarly, we can see the left child of root node is greater than its left child and smaller than its right child. So, it also satisfies the property of binary search tree. Therefore, we can say that the tree in the above image is a binary search tree.
Suppose if we change the value of node 35 to 55 in the above tree, check whether the tree will be binary search tree or not.
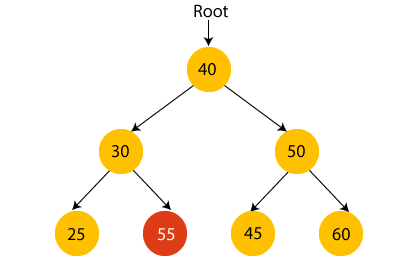
In the above tree, the value of root node is 40, which is greater than its left child 30 but smaller than right child of 30, i.e., 55. So, the above tree does not satisfy the property of Binary search tree. Therefore, the above tree is not a binary search tree.
Advantages of Binary search tree
- Searching an element in the Binary search tree is easy as we always have a hint that which subtree has the desired element.
- As compared to array and linked lists, insertion and deletion operations are faster in BST.
Example of creating a binary search tree
Now, let's see the creation of binary search tree using an example.
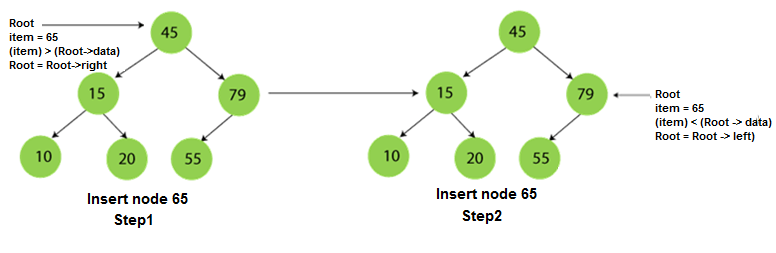
Suppose the data elements are - 45, 15, 79, 90, 10, 55, 12, 20, 50
- First, we have to insert 45 into the tree as the root of the tree.
- Then, read the next element; if it is smaller than the root node, insert it as the root of the left subtree, and move to the next element.
- Otherwise, if the element is larger than the root node, then insert it as the root of the right subtree.
Now, let's see the process of creating the Binary search tree using the given data element. The process of creating the BST is shown below -
Step 1 - Insert 45.

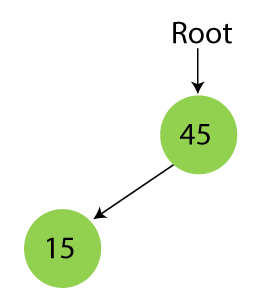
Step 2 - Insert 15.
As 15 is smaller than 45, so insert it as the root node of the left subtree.
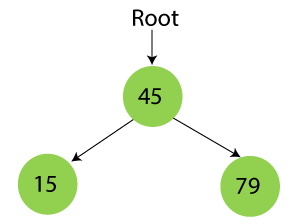
Step 3 - Insert 79.
As 79 is greater than 45, so insert it as the root node of the right subtree.
Step 4 - Insert 90.
90 is greater than 45 and 79, so it will be inserted as the right subtree of 79.
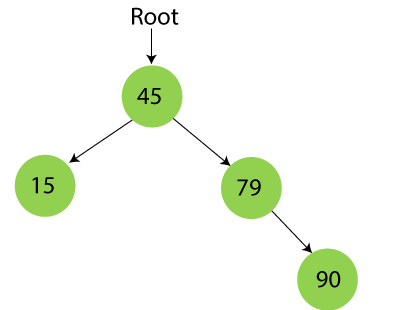
Step 5 - Insert 10.
10 is smaller than 45 and 15, so it will be inserted as a left subtree of 15.
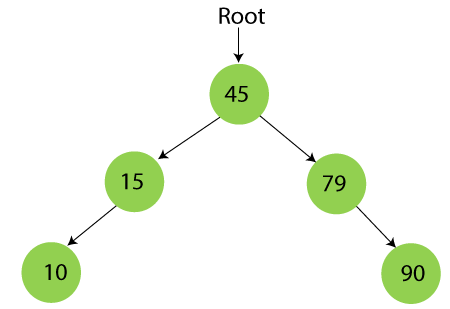
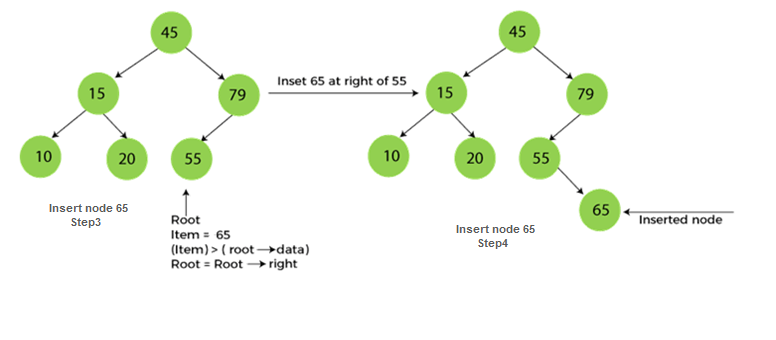
Step 6 - Insert 55.
55 is larger than 45 and smaller than 79, so it will be inserted as the left subtree of 79.
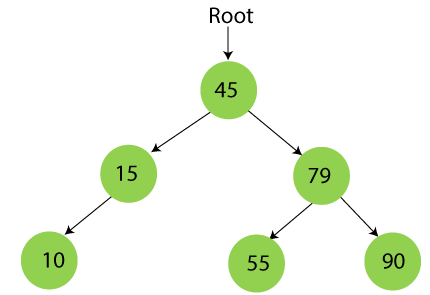
Step 7 - Insert 12.
12 is smaller than 45 and 15 but greater than 10, so it will be inserted as the right subtree of 10.
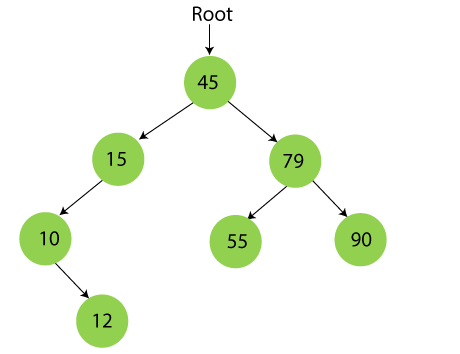
Step 8 - Insert 20.
20 is smaller than 45 but greater than 15, so it will be inserted as the right subtree of 15.
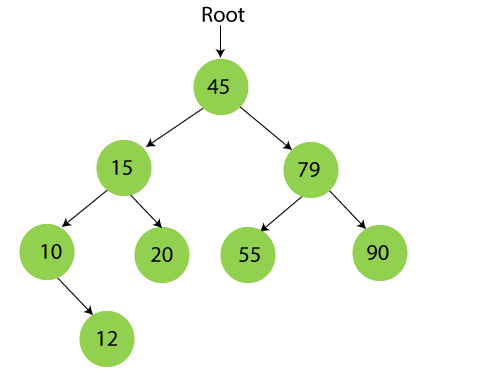
Step 9 - Insert 50.
50 is greater than 45 but smaller than 79 and 55. So, it will be inserted as a left subtree of 55.
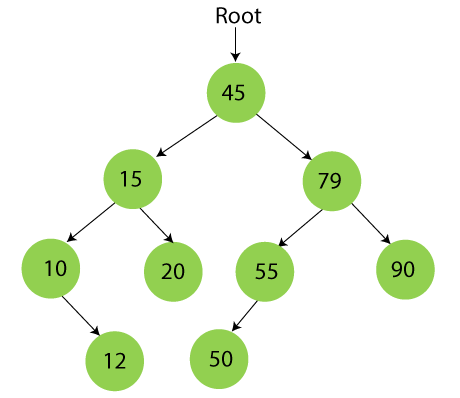
Now, the creation of binary search tree is completed. After that, let's move towards the operations that can be performed on Binary search tree.
We can perform insert, delete and search operations on the binary search tree.
Let's understand how a search is performed on a binary search tree.
Searching in Binary search tree
Searching means to find or locate a specific element or node in a data structure. In Binary search tree, searching a node is easy because elements in BST are stored in a specific order. The steps of searching a node in Binary Search tree are listed as follows -
- First, compare the element to be searched with the root element of the tree.
- If root is matched with the target element, then return the node's location.
- If it is not matched, then check whether the item is less than the root element, if it is smaller than the root element, then move to the left subtree.
- If it is larger than the root element, then move to the right subtree.
- Repeat the above procedure recursively until the match is found.
- If the element is not found or not present in the tree, then return NULL.
Now, let's understand the searching in binary tree using an example. We are taking the binary search tree formed above. Suppose we have to find node 20 from the below tree.
Step1:
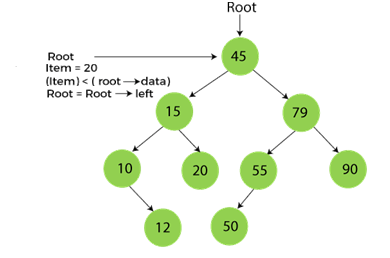
Step2:
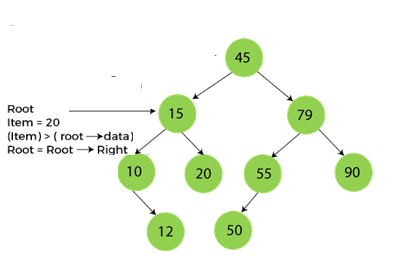
Step3:
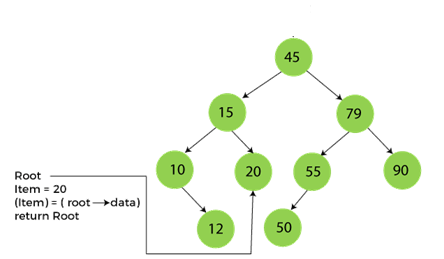
Now, let's see the algorithm to search an element in the Binary search tree.
Algorithm to search an element in Binary search tree
Search (root, item)
Step 1 - if (item = root → data) or (root = NULL)
return root
else if (item < root → data)
return Search(root → left, item)
else
return Search(root → right, item)
END if
Step 2 - END
Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.
Deletion in Binary Search tree
In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -
- The node to be deleted is the leaf node, or,
- The node to be deleted has only one child, and,
- The node to be deleted has two children
We will understand the situations listed above in detail.
When the node to be deleted is the leaf node
It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.
We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.
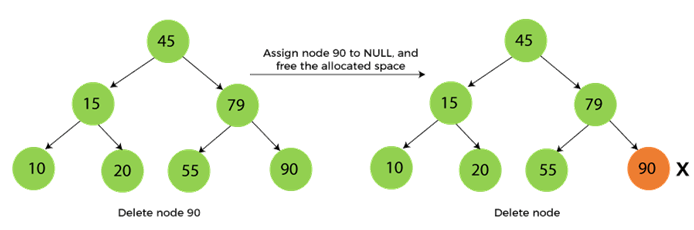
When the node to be deleted has only one child
In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.
We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.
So, the replaced node 79 will now be a leaf node that can be easily deleted.
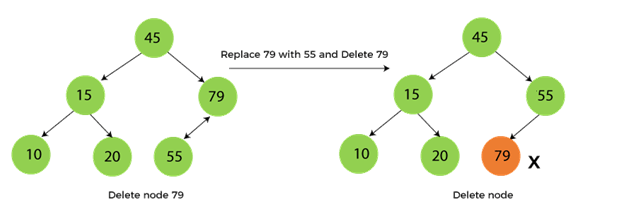
When the node to be deleted has two children
This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -
- First, find the inorder successor of the node to be deleted.
- After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.
- And at last, replace the node with NULL and free up the allocated space.
The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.
We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.
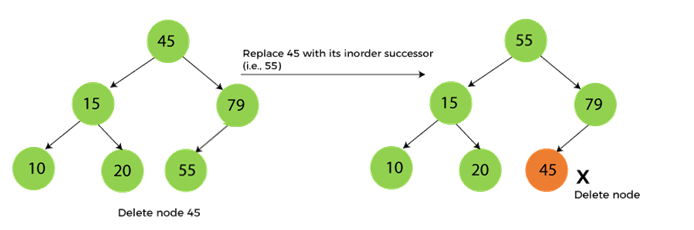
Now let's understand how insertion is performed on a binary search tree.
Insertion in Binary Search tree
A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.
Now, let's see the process of inserting a node into BST using an example.
The complexity of the Binary Search tree
Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.
1. Time Complexity
| Operations | Best case time complexity | Average case time complexity | Worst case time complexity |
|---|---|---|---|
| Insertion | O(log n) | O(log n) | O(n) |
| Deletion | O(log n) | O(log n) | O(n) |
| Search | O(log n) | O(log n) | O(n) |
Where 'n' is the number of nodes in the given tree.
2. Space Complexity
| Operations | Space complexity |
|---|---|
| Insertion | O(n) |
| Deletion | O(n) |
| Search | O(n) |
- The space complexity of all operations of Binary search tree is O(n).
Implementation of Binary search tree
Now, let's see the program to implement the operations of Binary Search tree.
Program: Write a program to perform operations of Binary Search tree in C++.
In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.
Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.
#include <iostream>
using namespace std;
struct Node {
int data;
Node *left;
Node *right;
};
Node* create(int item)
{
Node* node = new Node;
node->data = item;
node->left = node->right = NULL;
return node;
}
/*Inorder traversal of the tree formed*/
void inorder(Node *root)
{
if (root == NULL)
return;
inorder(root->left); //traverse left subtree
cout<< root->data << " "; //traverse root node
inorder(root->right); //traverse right subtree
}
Node* findMinimum(Node* cur) /*To find the inorder successor*/
{
while(cur->left != NULL) {
cur = cur->left;
}
return cur;
}
Node* insertion(Node* root, int item) /*Insert a node*/
{
if (root == NULL)
return create(item); /*return new node if tree is empty*/
if (item < root->data)
root->left = insertion(root->left, item);
else
root->right = insertion(root->right, item);
return root;
}
void search(Node* &cur, int item, Node* &parent)
{
while (cur != NULL && cur->data != item)
{
parent = cur;
if (item < cur->data)
cur = cur->left;
else
cur = cur->right;
}
}
void deletion(Node*& root, int item) /*function to delete a node*/
{
Node* parent = NULL;
Node* cur = root;
search(cur, item, parent); /*find the node to be deleted*/
if (cur == NULL)
return;
if (cur->left == NULL && cur->right == NULL) /*When node has no children*/
{
if (cur != root)
{
if (parent->left == cur)
parent->left = NULL;
else
parent->right = NULL;
}
else
root = NULL;
free(cur);
}
else if (cur->left && cur->right)
{
Node* succ = findMinimum(cur->right);
int val = succ->data;
deletion(root, succ->data);
cur->data = val;
}
else
{
Node* child = (cur->left)? cur->left: cur->right;
if (cur != root)
{
if (cur == parent->left)
parent->left = child;
else
parent->right = child;
}
else
root = child;
free(cur);
}
}
int main()
{
Node* root = NULL;
root = insertion(root, 45);
root = insertion(root, 30);
root = insertion(root, 50);
root = insertion(root, 25);
root = insertion(root, 35);
root = insertion(root, 45);
root = insertion(root, 60);
root = insertion(root, 4);
printf("The inorder traversal of the given binary tree is - \n");
inorder(root);
deletion(root, 25);
printf("\nAfter deleting node 25, the inorder traversal of the given binary tree is - \n");
inorder(root);
insertion(root, 2);
printf("\nAfter inserting node 2, the inorder traversal of the given binary tree is - \n");
inorder(root);
return 0;
}
Output
After the execution of the above code, the output will be -

So, that's all about the article. Hope the article will be helpful and informative to you.
Iterative Search in a Binary Search Tree
The function returns the pointer to the node if it finds the key, otherwise returns NULL. We saw how easy binary search trees make the process of searching and offers a best-case runtime complexity of logn.
The search function we studied was a recursive function, calling the function recursively on the left or the right subtree. But today, we’ll see the concept of searching iteratively in a binary search tree and its programming in C.
In the recursive approach, you start with the root and compare your key with the root node’s data, and if it's smaller than the key, you select the whole left subtree and start searching in it thinking of it as another smaller tree. But in an iterative approach, we have the tree intact the whole time. We just make a pointer run from the root to the place we expect our key to be. Let’s directly see the code for iterative search.
I have attached the source code below. Follow it as we proceed.
Understanding the code below:
- There is nothing much to explain in the code. Although for the people coming right here, we have just copied everything we had done till the last programming lecture which dealt with the search function. It had covered everything from creating a node, to building a tree. It also featured all the traversal methods, and all the other functions. We did this to save ourselves some time.
- Let’s create a binary search tree I’ve illustrated below using the createNode function. And without doing any further ado, we would move to creating the searchIter
Creating the function searchIter:
- Create a struct Node pointer function searchIter and pass into it the pointer to the root and the key you want to search as two of its parameters.
- First of all, check if the root’s data itself is the key we were looking for. If the root data is equal to the key, we have found the key, and we’ll return the pointer to the root.
- If we couldn’t find the key on the root, we’ll further see if our key is greater than or smaller than the root data. If it is smaller than the root data, we will make the root node pointer now point to the left child of the root, using the arrow operator. And if the key is greater than the root data, we’ll make the root node pointer point to the right child of the root
- And we’ll use a while loop to run steps 4 and 5 iteratively until our root becomes NULL, or we find the key and return from the function.
- And in the end, if we couldn’t find the key after iterating through the tree, or the root we received in the starting itself was a NULL, we would return NULL.
struct node * searchIter(struct node* root, int key){
while(root!=NULL){
if(key == root->data){
return root;
}
else if(key<root->data){
root = root->left;
}
else{
root = root->right;
}
}
return NULL;
}Code Snippet 1: Creating the searchIter function
Iteration is more intuitive because you are able to see what's exactly happening and how things end. Even so, recursion is considered a powerful tool.
Here is the whole source code:





No comments:
Post a Comment