Binary Tree Representations

Representing Binary Tree in memory

Let T be a Binary Tree. There are two ways of representing T in the memory as follow

1. Sequential Representation of Binary Tree.
2. Link Representation of Binary Tree.

1) Linked Representation of Binary Tree

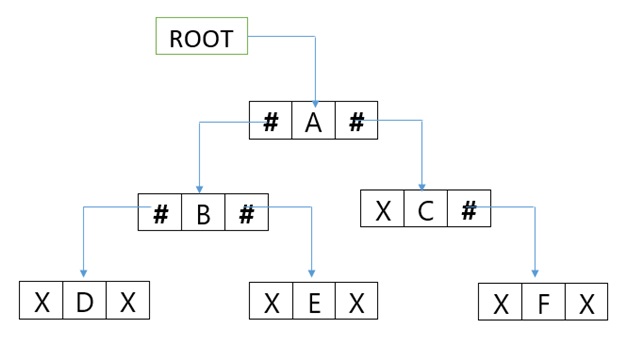
Consider a Binary Tree T. T will be maintained in memory by means of a linked list representation which uses three parallel arrays; INFO, LEFT, and RIGHT pointer variable ROOT as follows. In Binary Tree each node N of T will correspond to a location k such that

1. LEFT [k] contains the location of the left child of node N.
2. INFO [k] contains the data at the node N.
3. RIGHT [k] contains the location of right child of node N.

Representation of a node:

In this representation of binary tree root will contain the location of the root R of T. If any one of the subtree is empty, then the corresponding pointer will contain the null value if the tree T itself is empty, the ROOT will contain the null value.

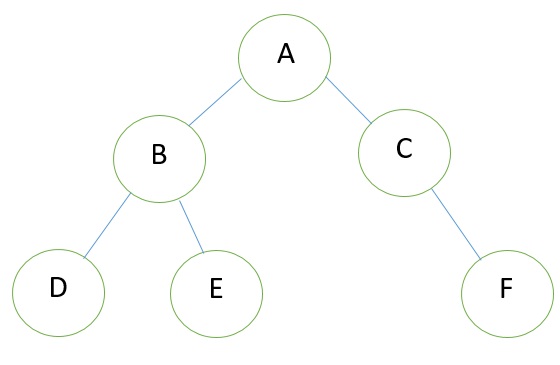
Example

Consider the binary tree T in the figure. A schematic diagram of the linked list representation of T appears in the following figure. Observe that each node is pictured with its three fields, and that the empty subtree is pictured by using x for null entries.

Binary Tree

Linked Representation of the Binary Tree

2) Sequential representation of Binary Tree

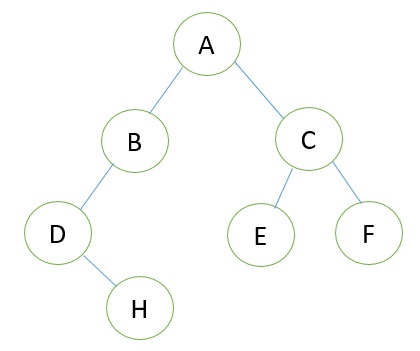
Let us consider that we have a tree T. let our tree T is a binary tree that us complete binary tree. Then there is an efficient way of representing T in the memory called the sequential representation or array representation of T. This representation uses only a linear array TREE as follows:

1. The root N of T is stored in TREE [1].
2. If a node occupies TREE [k] then its left child is stored in TREE [2 * k] and its right child is stored into TREE [2 * k + 1].

For Example:

Consider the following Tree:

Its sequential representation is as follow: