Binomial Heap

A binomial heap is a specific implementation of the heap data structure. Binomial heaps are collections of binomial trees that are linked together where each tree is an ordered heap. In a binomial heap, there are either one or zero binomial trees of order $�,$ where $�$ helps describe the number of elements a given tree can have: $2^{�}$. 

Binomial heaps are similar to binary heaps but binomial heaps have a more specific structure and allow for efficient merging of heaps. Heaps are often used to implement priority queues which are in turn used in implementations of many types of algorithms such as shortest-path finding algorithms—these fast operations help make these algorithms more efficient.

Binomial Trees

Binomial heaps are made up of binomial trees.

A binomial tree ${�}_{�}$ is made up of two binomial trees ${�}_{�-1}$ that are linked together such that the root of one is the leftmost child of the root of the other.

Binomial trees are defined recursively as follows:

• A binomial tree of order 0 is a single node.
• A binomial tree of order k has a root node whose children are roots of binomial trees of orders k−1, k−2, ..., 2, 1, 0 (in this order).

The image below is a collection of binomial trees with orders 0, 1, 2, and 3 (from left to right). The order represents how many children the root node is able to have. For example, there are three children coming out of the order 3 node and no children coming out of the order 0 node.

In this diagram, binomial trees of order 0 to 3 are shown, with their subtrees highlighted: subtrees of different order have different highlight colors. For example, the order 3 binomial tree is connected to an order 2, 1, and 0 (highlighted as blue, green and red respectively) binomial tree.

Properties of Binomial Trees:

An order $�$ binomial tree ${�}_{�}$ has the following properties:

• The height of the tree is $�$. For example, in the image above, if the tree only contained the 0${}^{\text{th}}$ order node, the height would be $0$. Since the entire tree is order $3$, the height is $3.$
• There are a total of $2^{�}$ nodes in the tree.
• The tree has kCi nodes at depth $�\mathrm{.}$i for i = 0, 1, . . . , k.
• The degree of the root is $�\mathrm{.}$
• Deleting the root yields $�$ binomial trees: ${�}_{�}-1,\cdots ,{�}_0\mathrm{.}$

Binomial Heaps:

Binomial heaps can be implemented by using doubly linked lists to store the root nodes. Each node stores information about the parent pointer, left and right sibling pointers, left most child pointer, the number of children it has, and its key. Since the list is doubly linked, the parent nodes have pointers to the children and the children have pointers to the parent. Using the doubly linked list allows for constant time inserts and deletes from the root list, constant time to merge for two root lists together, and more.

The structure of a binomial heap is similar to the binary number system. For example, a binomial heap containing $63$ elements will contain binomial trees of order $1,2,3,4,5,$ and $6$ since it takes six digits to write the decimal number 63 in binary. 63 in binary is 111111.

Properties of Binomial Heaps:

For a binomial heap with $�$ nodes,

• the node containing the minimum element is a root of either ${�}_0,{�}_1,\dots$ or ${�}_{�};$
• in total, the heap has  binomial trees;
• the height of the heap is 

A binomial heap must satisfy the binomial heap property. The property is as follows:

Binomial Heap Property

• Every binomial tree in a binomial min heap obeys the min-heap property (that the key of a node is greater than or equal to the key of its parent) and every binomial tree in a binomial max heap obeys the max-heap property (that the key of a node is less than or equal to the key of its parent).

• There can only be either one or zero binomial trees for each order. In other words, for every $�$, there is at most one binomial tree of order $�$ in the heap.

The first property ensures that the min/max-heap properties hold throughout the heap.

The second property implies that a binomial heap with $�$ nodes consists of at most $\log �+1$ binomial trees, which is a property of binomial heaps. In order to maintain this property, the heaps may need to be consolidated after an operation. For example, if an operation results in two heaps of order two, steps must be taken to correct this so that the binomial heap property holds.

Example of a binomial heap containing 13 nodes with distinct keys. The heap consists of three binomial trees with orders 0, 2, and 3.

The children of a node are linked together in a doubly linked list. Each child has a pointer to its parent, and the parent has a pointer to one of the children. Here is what the above binomial heap looks like as a linked list of the roots: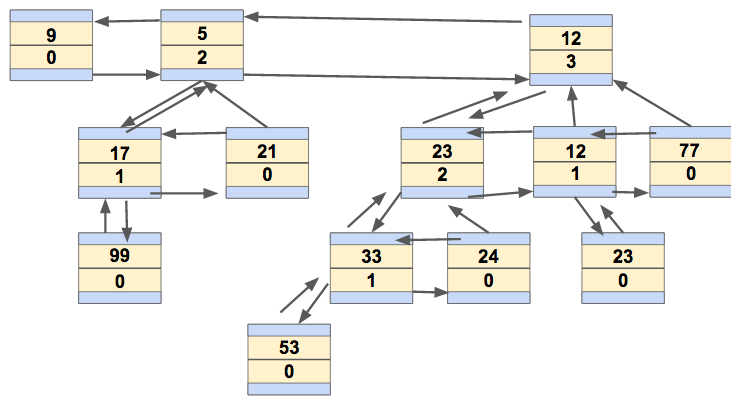

Operations on binomial heaps

Creating a new binomial heap

To make an empty binomial heap, the MAKE-BINOMIAL-HEAP procedure simply allocates and returns an object H, where head[H] = NIL. The running time is θ(1).

Finding the minimum key

The procedure BINOMIAL-HEAP-MINIMUM returns a pointer to the node with the minimum key in an n-node binomial heap H. This implementation assumes that there are no keys with value ∞.

BINOMIAL-HEAP-MINIMUM(H)

1  y = NIL
2  x = head[H]
3  min = ∞  
4  while x ≠ NIL
5      do if key[x] < min
6            then min = key[x]
7                 y = x
8         x = sibling[x]
9  return y

Since a binomial heap is heap-ordered, the minimum key must reside in a root node. The BINOMIAL-HEAP-MINIMUM procedure checks all roots, which number at most ⌊lg n⌋+1, saving the current minimum in min and a pointer to the current minimum in y.

Because there are at most ⌊lg n⌋+1 roots to check, the running time of BINOMIAL-HEAP-MINIMUM is O(lg n).

Uniting two binomial heaps

The operation of uniting two binomial heaps is used as a subroutine by most of the remaining operations. The BINOMIAL-HEAP-UNION procedure repeatedly links binomial trees whose roots have the same degree. The following procedure links the Bk-1 tree rooted at node y to the Bk-1 tree rooted at node z; that is, it makes z the parent of y. Node z thus becomes the root of a Bk tree.

BINOMIAL-LINK(y,z)

1  p[y] = z
2  sibling[y] = child[z]
3  child[z] = y
4  degree[z] = degree[z]+1

The BINOMIAL-LINK procedure makes node y the new head of the linked list of node z's children in O(1) time. It works because the left-child, right-sibling representation of each binomial tree matches the ordering property of the tree: in a Bk tree, the leftmost child of the root is the root of a Bk-1 tree.

The following procedure unites binomial heaps H1 and H2, returning the resulting heap. It destroys the representations of H1 and H2 in the process. Besides BINOMIAL-LINK, the procedure uses an auxiliary procedure BINOMIAL-HEAP-MERGE that merges the root lists of H1 and H2 into a single linked list that is sorted by degree into monotonically increasing order.

Union function in Binomial Heap:

To perform the union of two binomial heaps, we have to consider the below cases -

Case 1: If degree[x] is not equal to degree[next x], then move pointer ahead.

Case 2: if degree[x] = degree[next x] = degree[sibling(next x)] then,Move the pointer ahead.

Case 3: If degree[x] = degree[next x] but not equal to degree[sibling[next x]]

and key[x] < key[next x] then remove [next x] from root and attached to x.

Case 4: If degree[x] = degree[next x] but not equal to degree[sibling[next x]]

and key[x] > key[next x] then remove x from root and attached to [next x].

Example. Consider two binomial heaps -

Insert an element in the heap

The following procedure inserts node x into binomial heap H, assuming of course that node x has already been allocated and key[x] has already been filled in.

BINOMIAL-HEAP-INSERT(H,x)

1  H'  MAKE-BINOMIAL-HEAP()
2  p[x]  NIL
3  child[x]  NIL
4  sibling[x]  NIL
5  degree[x]  0
6  head[H']  x
7  H  BINOMIAL-HEAP-UNION(H,H')

The procedure simply makes a one-node binomial heap H' in O(1) time and unites it with the n-node binomial heap H in O(1g n) time. The call to BINOMIAL-HEAP-UNION takes care of freeing the temporary binomial heap H'. 

Inserting an element in the heap can be done by simply creating a new heap only with the element to be inserted, and then merging it with the original heap. Due to the merging, the single insertion in a heap takes O(logn) time. Now, let's understand the process of inserting a new node in a heap using an example.

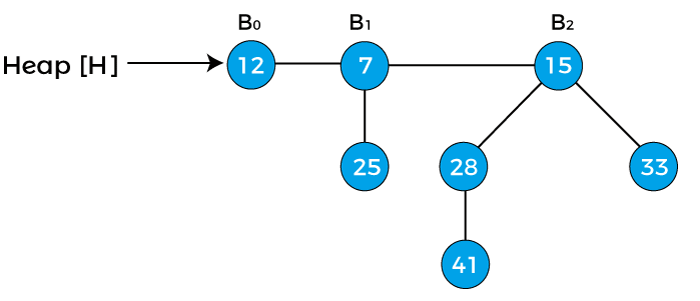
In the above heap, there are three binomial trees of degrees 0, 1, and 2 are given where B0 is attached to the head of the heap.

Suppose we have to insert node 15 in the above heap.

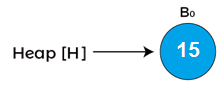
First, we have to combine both of the heaps. As both node 12 and node 15 are of degree 0, so node 15 is attached to node 12 as shown below -

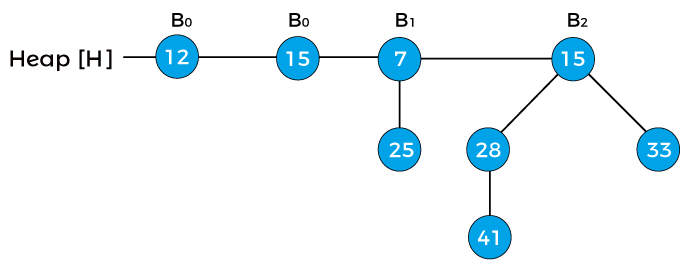
Now, assign x to B₀ with value 12, next(x) to B₀ with value 15, and assign sibling(next(x)) to B₁ with value 7. As the degree of x and next(x) is equal. The key value of x is smaller than the key value of next(x), so next(x) is removed and attached to the x. It is shown in the below image -

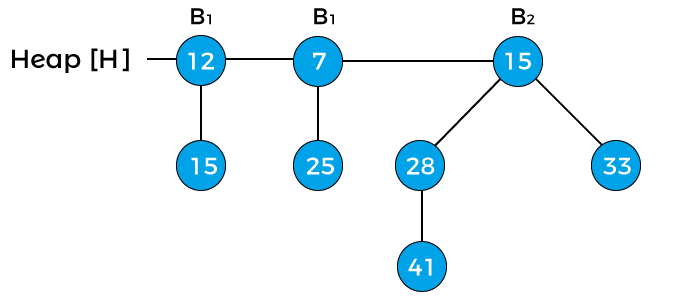
Now, x points to node 12 with degree B₁, next(x) to node 7 with degree B₁, and sibling(next(x)) points to node 15 with degree B₂. The degree of x is equal to the degree of next(x) but not equal to the degree of sibling(next(x)). The key value of x is greater than the key value of next(x); therefore, x is removed and attached to the next(x) as shown in the below image -

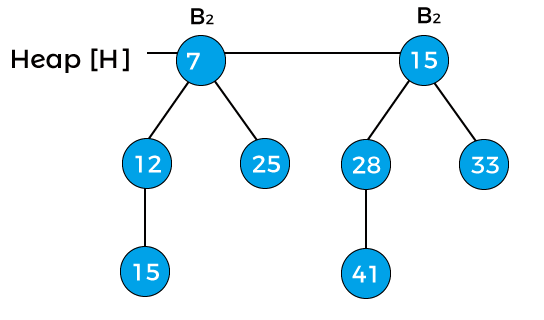
Now, x points to node 7, and next(x) points to node 15. The degree of both x and next(x) is B₂, and the key value of x is less than the key value of next(x), so next(x) will be removed and attached to x as shown in the below image -

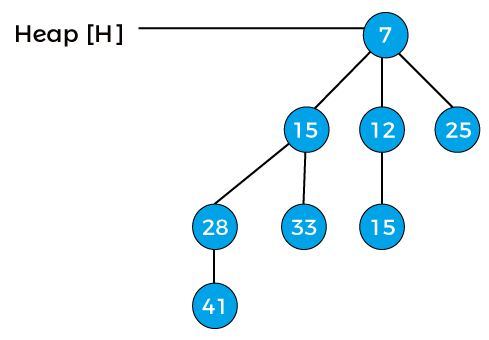
Now, the degree of the above heap is B₃, and it is the final binomial heap after inserting node 15.

Extracting the minimum key

The following procedure extracts the node with the minimum key from binomial heap H and returns a pointer to the extracted node.

BINOMIAL-HEAP-EXTRACT-MIN(H)

1  find the root x with the minimum key in the root list of H,
and remove x from the root list of H
2  H' = MAKE-BINOMIAL-HEAP()
3  reverse the order of the linked list of x's children,
and set head[H'] to point to the head of the resulting list
4  H = BINOMIAL-HEAP-UNION(H,H')
5  return x

It means that we have to remove an element with the minimum key value. As we know, in min-heap, the root element contains the minimum key value. So, we have to compare the key value of the root node of all the binomial trees. Let's see an example of extracting the minimum key from the heap.

Suppose the heap is -

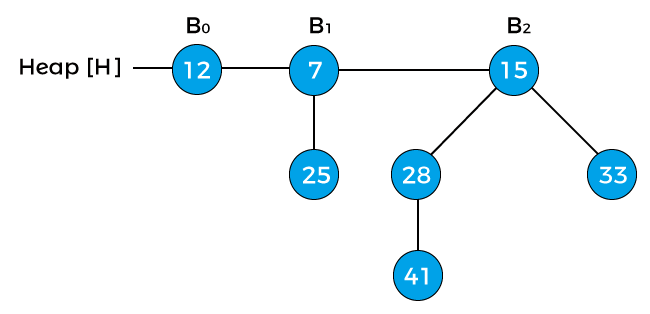
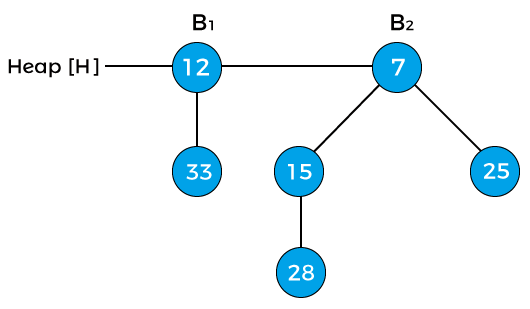
Now, compare the key values of the root node of the binomial trees in the above heap. So, 12, 7, and 15 are the key values of the root node in the above heap in which 7 is minimum; therefore, remove node 7 from the tree as shown in the below image -

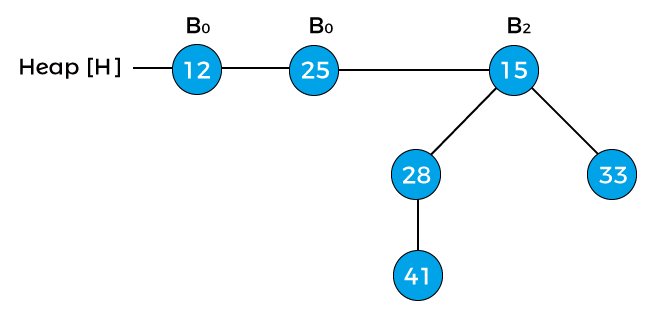
Now, the degree of node 12 and node 25 is B₀, and the degree of node 15 is B₂. Pointer x points to the node 12, next(x) points to the node 25, and sibling(next(x)) points to the node 15. Since the degree of x is equal to the degree of next(x) but not equal to the degree of sibling(next(x)). Value of pointer x is less than the pointer next(x), so node 25 will be removed and attached to node 12 as shown in the below image -

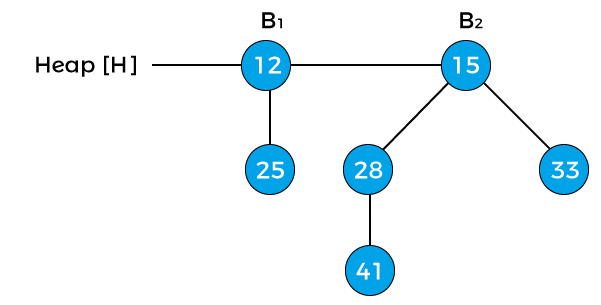
Now, the degree of node 12 is changed to B₁. The above heap is the final heap after extracting the minimum key.

Decreasing a key

The following procedure decreases the key of a node x in a binomial heap H to a new value k. It signals an error if k is greater than x's current key.

BINOMIAL-HEAP-DECREASE-KEY (H,x,k)

1  if k > key[x]
2      then error "new key is greater than current key"
3  key[x] = k
4  y = x
5  z = p[y]
6  while z  NIL and key[y] < key[z]
7      do exchange key[y] <--> key[z]
8          If y and z have satellite fields, exchange them, too.
9         y = z
10        z = p[y]

Now, let's move forward to another operation to be performed on binomial heap. Once the value of the key is decreased, it might be smaller than its parent's key that results in the violation of min-heap property. If such case occurs after decreasing the key, then exchange the element with its parent, grandparent, and so on until the min-heap property is satisfied.

Let's understand the process of decreasing a key in a binomial heap using an example. Consider a heap given below -

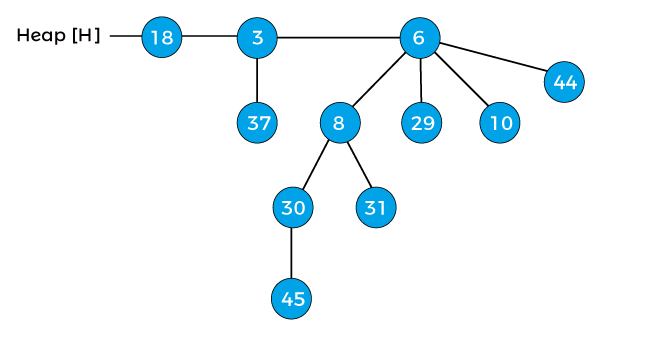
Decrease the key 45 by 7 of the above heap. After decreasing 45 by 7, the heap will be -

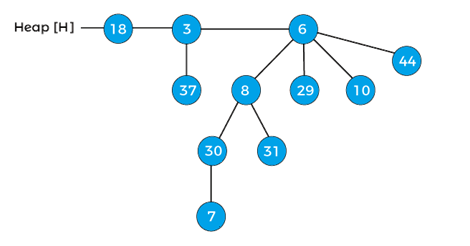
After decreasing the key, the min-heap property of the above heap is violated. Now, compare 7 wits its parent 30, as it is lesser than the parent, swap 7 with 30, and after swapping, the heap will be -

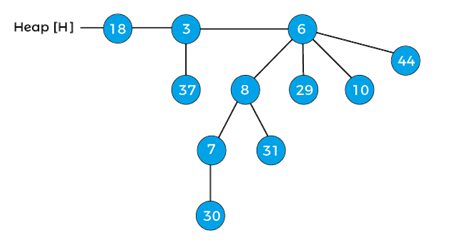
Again compare the element 7 with its parent 8, again it is lesser than the parent, so swap the element 7 with its parent 8, after swapping the heap will be -

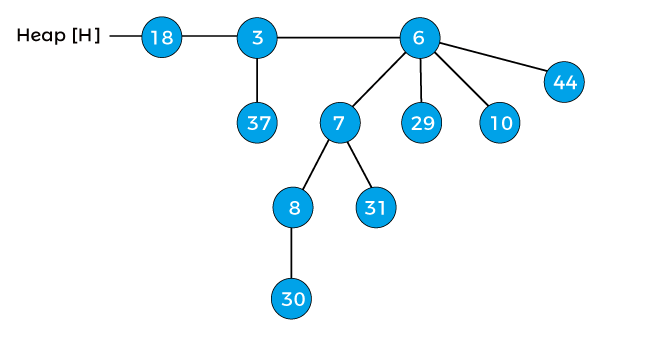
Now, the min-heap property of the above heap is satisfied. So, the above heap is the final heap after decreasing a key.

Deleting a node from the heap

To delete a node from the heap, first, we have to decrease its key to negative infinity (or -∞) and then delete the minimum in the heap. Now we will see how to delete a node with the help of an example. Consider the below heap, and suppose we have to delete the node 41 from the heap -

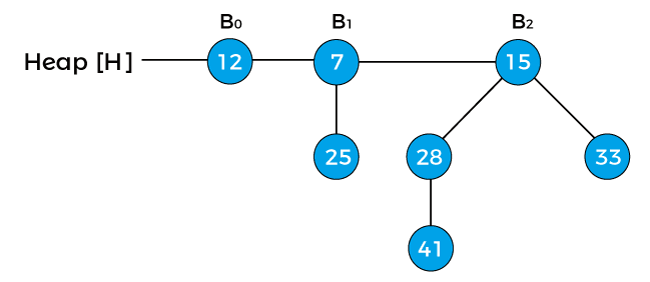
First, replace the node with negative infinity (or -∞) as shown below -

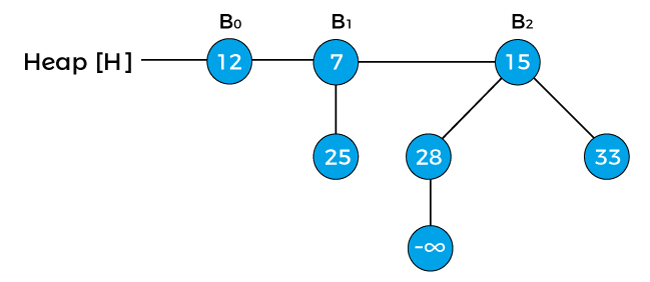
Now, swap the negative infinity with its root node in order to maintain the min-heap property.

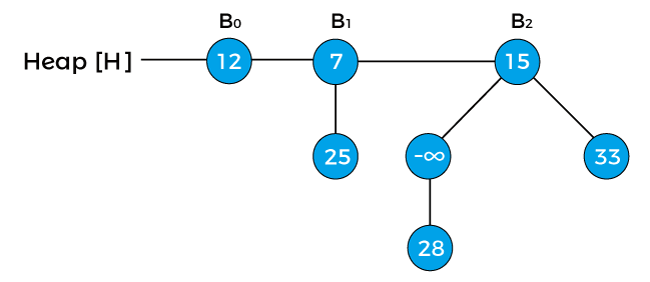
Now, again swap the negative infinity with its root node.

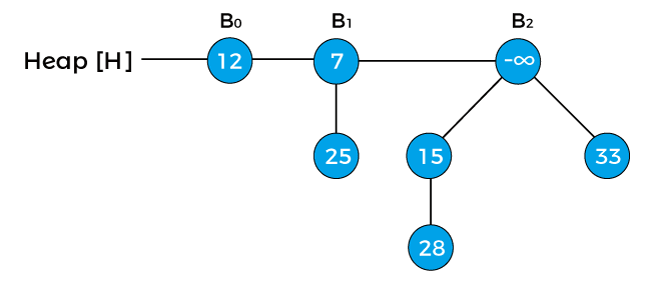
The next step is to extract the minimum key from the heap. Since the minimum key in the above heap is -infinity so we will extract this key, and the heap would be:

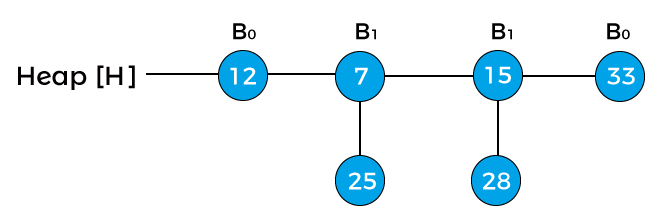
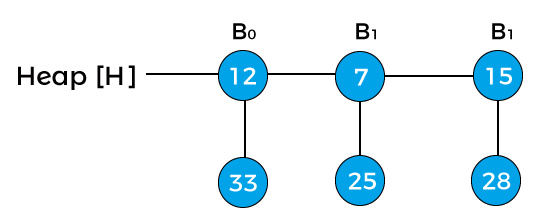
The above is the final heap after deleting the node 41.

Complexity of binomial heap

Now, let's see the time complexity of the operations performed on binomial heap.

Time Complexity

Operations	Time complexity
Finding the minimum key	O(log n)
Inserting a node	O(log n)
Extracting minimum key	O(log n)
Decreasing a key	O(log n)
Union or merging	O(log n)
Deleting a node	O(log n)

The time complexity of finding the minimum element from the heap can be reduced to O(1). It can be done by using an additional pointer to the minimum element.

Space Complexity

The space complexity of a binomial heap with 'n' elements is O(n).