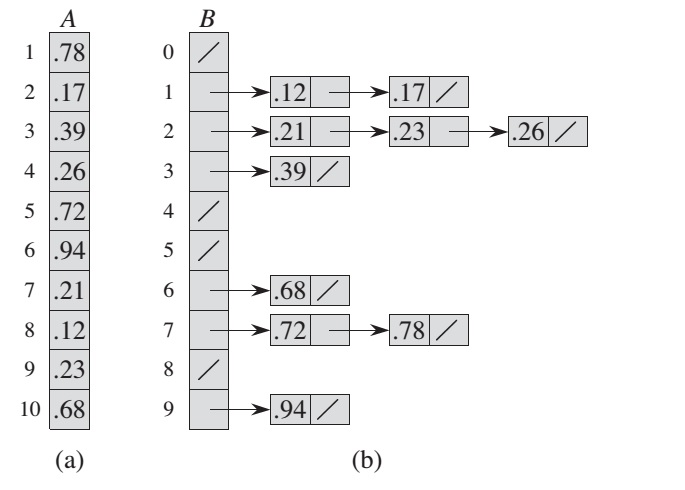
Bucket Sort

Bucket Sort

Bucket sort assumes that the input is drawn from a uniform distribution and has an average-case running time of O(n). Like counting sort, bucket sort is fast because it assumes something about the input.

BUCKET-SORT(A):
let B[0..n-1] be a new array
n = A.length
for i = 0 to n - 1
   make B[i] an empty list
for i = 1 to n
   insert A[i] into list B[floor(n * A[i])]
for i = 0 to n - 1
   sort list B[i] with insertion sort
concatenate the list B[0], B[1], ..., B[n-1] together in order

Detail calculations:

0.72 * 10 = 7.2 -> ceil() -> 7
0.17 * 10 = 1.7 -> ceil() -> 1
...
...
0.68 * 10 = 6.8 -> ceil() -> 6

To analyze the cost of the calls to insertion sort, let n[i] be the random variable denoting the number of elements placed in bucket B[i]. Since insertion sort runs in quadratic time. As conclusion the average-case running time for bucket sort is:

O(n) + n * O(2 - 1/n) = O(n)

Even if the input is not drawn from a uniform distribution, bucket sort may still run in linear time. As long as the input has the property that the sum of the sum squares of the bucket sizes is linear in the total number of elements.

The disadvantage is that if you get a bad distribution into the buckets, you may end up doing a huge amount of extra work for no benefit or a minimal benefit. As a result, bucket sort works best when the data are more or less uniformly distributed or where there is an intelligent way to choose the buckets given a quick set of heuristics based on the input array