Dijkstra's Algorithm

It is a greedy algorithm that solves the single-source shortest path problem for a directed graph G = (V, E) with nonnegative edge weights, i.e., w (u, v) ≥ 0 for each edge (u, v) ∈ E.

Dijkstra's Algorithm maintains a set S of vertices whose final shortest - path weights from the source s have already been determined. That's for all vertices v ∈ S; we have d [v] = δ (s, v). The algorithm repeatedly selects the vertex u ∈ V - S with the minimum shortest - path estimate, insert u into S and relaxes all edges leaving u.

Because it always chooses the "lightest" or "closest" vertex in V - S to insert into set S, it is called as the greedy strategy.

RELAX(u, v, w)

1.       If v.d > u.d + w(u,v)

a.       v.d = u.d + w(u,v)

b.      v.π=u

Analysis: The running time of Dijkstra's algorithm on a graph with edges E and vertices V can be expressed as a function of |E| and |V| using the Big - O notation. The simplest implementation of the Dijkstra's algorithm stores vertices of set Q in an ordinary linked list or array, and operation Extract - Min (Q) is simply a linear search through all vertices in Q. In this case, the running time is O (|V² |+|E|=O(V² ).

Here is an example of Dijkstra's Algorithm

Let's understand the working of Dijkstra's algorithm. Consider the below graph.

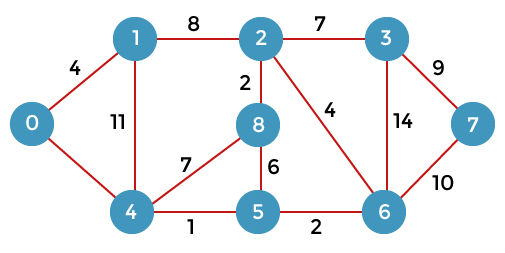
First, we have to consider any vertex as a source vertex. Suppose we consider vertex 0 as a source vertex.

Here we assume that 0 as a source vertex, and distance to all the other vertices is infinity. Initially, we do not know the distances. First, we will find out the vertices which are directly connected to the vertex 0. As we can observe in the above graph that two vertices are directly connected to vertex 0.

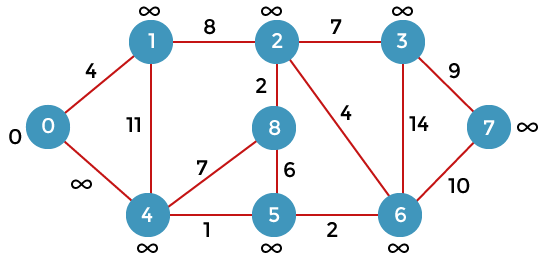
Let's assume that the vertex 0 is represented by 'x' and the vertex 1 is represented by 'y'. The distance between the vertices can be calculated by using the below formula:

d(x, y) = d(x) + c(x, y) < d(y)

= (0 + 4) < ∞

= 4 < ∞

Since 4<∞ so we will update d(v) from ∞ to 4.

Therefore, we come to the conclusion that the formula for calculating the distance between the vertices:

{if( d(u) + c(u, v) < d(v))

d(v) = d(u) +c(u, v) }

Now we consider vertex 0 same as 'x' and vertex 4 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (0 + 8) < ∞

= 8 < ∞

Therefore, the value of d(y) is 8. We replace the infinity value of vertices 1 and 4 with the values 4 and 8 respectively. Now, we have found the shortest path from the vertex 0 to 1 and 0 to 4. Therefore, vertex 0 is selected. Now, we will compare all the vertices except the vertex 0. Since vertex 1 has the lowest value, i.e., 4; therefore, vertex 1 is selected.

Since vertex 1 is selected, so we consider the path from 1 to 2, and 1 to 4. We will not consider the path from 1 to 0 as the vertex 0 is already selected.

First, we calculate the distance between the vertex 1 and 2. Consider the vertex 1 as 'x', and the vertex 2 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (4 + 8) < ∞

= 12 < ∞

Since 12<∞ so we will update d(2) from ∞ to 12.

Now, we calculate the distance between the vertex 1 and vertex 4. Consider the vertex 1 as 'x' and the vertex 4 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (4 + 11) < 8

= 15 < 8

Since 15 is not less than 8, we will not update the value d(4) from 8 to 12.

Till now, two nodes have been selected, i.e., 0 and 1. Now we have to compare the nodes except the node 0 and 1. The node 4 has the minimum distance, i.e., 8. Therefore, vertex 4 is selected.

Since vertex 4 is selected, so we will consider all the direct paths from the vertex 4. The direct paths from vertex 4 are 4 to 0, 4 to 1, 4 to 8, and 4 to 5. Since the vertices 0 and 1 have already been selected so we will not consider the vertices 0 and 1. We will consider only two vertices, i.e., 8 and 5.

First, we consider the vertex 8. First, we calculate the distance between the vertex 4 and 8. Consider the vertex 4 as 'x', and the vertex 8 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (8 + 7) < ∞

= 15 < ∞

Since 15 is less than the infinity so we update d(8) from infinity to 15.

Now, we consider the vertex 5. First, we calculate the distance between the vertex 4 and 5. Consider the vertex 4 as 'x', and the vertex 5 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (8 + 1) < ∞

= 9 < ∞

Since 5 is less than the infinity, we update d(5) from infinity to 9.

Till now, three nodes have been selected, i.e., 0, 1, and 4. Now we have to compare the nodes except the nodes 0, 1 and 4. The node 5 has the minimum value, i.e., 9. Therefore, vertex 5 is selected.

Since the vertex 5 is selected, so we will consider all the direct paths from vertex 5. The direct paths from vertex 5 are 5 to 8, and 5 to 6.

First, we consider the vertex 8. First, we calculate the distance between the vertex 5 and 8. Consider the vertex 5 as 'x', and the vertex 8 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (9 + 15) < 15

= 24 < 15

Since 24 is not less than 15 so we will not update the value d(8) from 15 to 24.

Now, we consider the vertex 6. First, we calculate the distance between the vertex 5 and 6. Consider the vertex 5 as 'x', and the vertex 6 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (9 + 2) < ∞

= 11 < ∞

Since 11 is less than infinity, we update d(6) from infinity to 11.

Till now, nodes 0, 1, 4 and 5 have been selected. We will compare the nodes except the selected nodes. The node 6 has the lowest value as compared to other nodes. Therefore, vertex 6 is selected.

Since vertex 6 is selected, we consider all the direct paths from vertex 6. The direct paths from vertex 6 are 6 to 2, 6 to 3, and 6 to 7.

First, we consider the vertex 2. Consider the vertex 6 as 'x', and the vertex 2 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (11 + 4) < 12

= 15 < 12

Since 15 is not less than 12, we will not update d(2) from 12 to 15

Now we consider the vertex 3. Consider the vertex 6 as 'x', and the vertex 3 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (11 + 14) < ∞

= 25 < ∞

Since 25 is less than ∞, so we will update d(3) from ∞ to 25.

Now we consider the vertex 7. Consider the vertex 6 as 'x', and the vertex 7 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (11 + 10) < ∞

= 22 < ∞

Since 22 is less than ∞ so, we will update d(7) from ∞ to 22.

Till now, nodes 0, 1, 4, 5, and 6 have been selected. Now we have to compare all the unvisited nodes, i.e., 2, 3, 7, and 8. Since node 2 has the minimum value, i.e., 12 among all the other unvisited nodes. Therefore, node 2 is selected.

Since node 2 is selected, so we consider all the direct paths from node 2. The direct paths from node 2 are 2 to 8, 2 to 6, and 2 to 3.

First, we consider the vertex 8. Consider the vertex 2 as 'x' and 8 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (12 + 2) < 15

= 14 < 15

Since 14 is less than 15, we will update d(8) from 15 to 14.

Now, we consider the vertex 6. Consider the vertex 2 as 'x' and 6 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (12 + 4) < 11

= 16 < 11

Since 16 is not less than 11 so we will not update d(6) from 11 to 16.

Now, we consider the vertex 3. Consider the vertex 2 as 'x' and 3 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (12 + 7) < 25

= 19 < 25

Since 19 is less than 25, we will update d(3) from 25 to 19.

Till now, nodes 0, 1, 2, 4, 5, and 6 have been selected. We compare all the unvisited nodes, i.e., 3, 7, and 8. Among nodes 3, 7, and 8, node 8 has the minimum value. The nodes which are directly connected to node 8 are 2, 4, and 5. Since all the directly connected nodes are selected so we will not consider any node for the updation.

The unvisited nodes are 3 and 7. Among the nodes 3 and 7, node 3 has the minimum value, i.e., 19. Therefore, the node 3 is selected. The nodes which are directly connected to the node 3 are 2, 6, and 7. Since the nodes 2 and 6 have been selected so we will consider these two nodes.

Now, we consider the vertex 7. Consider the vertex 3 as 'x' and 7 as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (19 + 9) < 21

= 28 < 21

Since 28 is not less than 21, so we will not update d(7) from 28 to 21.

Directed Graph Example:

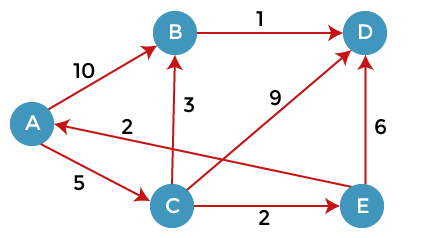
Here, we consider A as a source vertex. A vertex is a source vertex so entry is filled with 0 while other vertices filled with ∞. The distance from source vertex to source vertex is 0, and the distance from the source vertex to other vertices is ∞.

We will solve this problem using the below table:

A	B	C	D	E
∞	∞	∞	∞	∞

Since 0 is the minimum value in the above table, so we select vertex A and added in the second row shown as below:

	A	B	C	D	E
A	0	∞	∞	∞	∞

As we can observe in the above graph that there are two vertices directly connected to the vertex A, i.e., B and C. The vertex A is not directly connected to the vertex E, i.e., the edge is from E to A. Here we can calculate the two distances, i.e., from A to B and A to C. The same formula will be used as in the previous problem.

If(d(x) + c(x, y)  < d(y))  

  Then we update d(y) = d(x) + c(x, y)   

 

	A	B	C	D	E
A	0	∞	∞	∞	∞
		10	5	∞	∞

As we can observe in the third row that 5 is the lowest value so vertex C will be added in the third row.

We have calculated the distance of vertices B and C from A. Now we will compare the vertices to find the vertex with the lowest value. Since the vertex C has the minimum value, i.e., 5 so vertex C will be selected.

Since the vertex C is selected, so we consider all the direct paths from the vertex C. The direct paths from the vertex C are C to B, C to D, and C to E.

First, we consider the vertex B. We calculate the distance from C to B. Consider vertex C as 'x' and vertex B as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (5 + 3) < ∞

= 8 < ∞

Since 8 is less than the infinity so we update d(B) from ∞ to 8. Now the new row will be inserted in which value 8 will be added under the B column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
		10	5	∞	∞
		8

We consider the vertex D. We calculate the distance from C to D. Consider vertex C as 'x' and vertex D as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (5 + 9) < ∞

= 14 < ∞

Since 14 is less than the infinity so we update d(D) from ∞ to 14. The value 14 will be added under the D column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
		8		14

We consider the vertex E. We calculate the distance from C to E. Consider vertex C as 'x' and vertex E as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (5 + 2) < ∞

= 7 < ∞

Since 14 is less than the infinity so we update d(D) from ∞ to 14. The value 14 will be added under the D column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
		8		14	7

As we can observe in the above table that 7 is the minimum value among 8, 14, and 7. Therefore, the vertex E is added on the left as shown in the below table:

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
E		8		14	7

The vertex E is selected so we consider all the direct paths from the vertex E. The direct paths from the vertex E are E to A and E to D. Since the vertex A is selected, so we will not consider the path from E to A.

Consider the path from E to D.

d(x, y) = d(x) + c(x, y) < d(y)

= (7 + 6) < 14

= 13 < 14

Since 13 is less than the infinity so we update d(D) from ∞ to 13. The value 13 will be added under the D column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
E		8		14	7
B		8		13

The value 8 is a minimum between 8 and 13. Therefore, vertex B is selected. The direct path from B is B to D.

d(x, y) = d(x) + c(x, y) < d(y)

= (8 + 1) < 13

= 9 < 13

Since 9 is less than 13 so we update d(D) from 13 to 9. The value 9 will be added under the D column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
E		8		14	7
B		8		13
D				9

The disadvantage of Dijkstra's Algorithm:

1. It does a blind search, so wastes a lot of time while processing.
2. It can't handle negative edges.
3. It leads to the acyclic graph and most often cannot obtain the right shortest path.
4. We need to keep track of vertices that have been visited.