Relaxation

The single - source shortest paths are based on a technique known as relaxation, a method that repeatedly decreases an upper bound on the actual shortest path weight of each vertex until the upper bound equivalent the shortest - path weight. For each vertex v ∈ V, we maintain an attribute d [v], which is an upper bound on the weight of the shortest path from source s to v. We call d [v] the shortest path estimate.

INITIALIZE - SINGLE - SOURCE (G, s)

 1. for each vertex v ∈ V [G]
 2. do d [v] ← ∞
 3. π [v] ← NIL
 4. d [s] ← 0

After initialization, π [v] = NIL for all v ∈ V, d [v] = 0 for v = s, and d [v] = ∞ for v ∈ V - {s}.

The development of relaxing an edge (u, v) consists of testing whether we can improve the shortest path to v found so far by going through u and if so, updating d [v] and π [v]. A relaxation step may decrease the value of the shortest - path estimate d [v] and updated v's predecessor field π [v].

Fig: Relaxing an edge (u, v) with weight w (u, v) = 2. The shortest-path estimate of each vertex appears within the vertex.

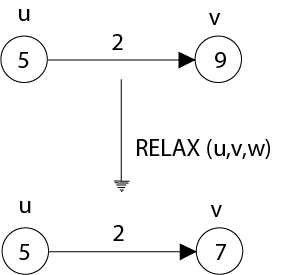
(a) Because v. d > u. d + w (u, v) prior to relaxation, the value of v. d decreases

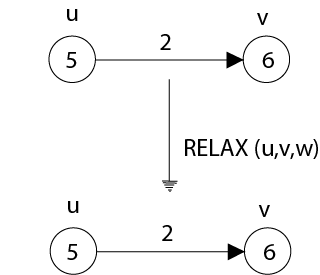
(b) Here, v. d < u. d + w (u, v) before relaxing the edge, and so the relaxation step leaves v. d unchanged.

The subsequent code performs a relaxation step on edge (u, v)

RELAX (u, v, w)

 1. If d [v] > d [u] + w (u, v)
 2. then d [v] ← d [u] + w (u, v)
 3. π [v] ← u