Let the vertices of G be V = {1, 2........n} and consider a subset {1, 2........k} of vertices for some k. For any pair of vertices i, j ∈ V, considered all paths from i to j whose intermediate vertices are all drawn from {1, 2.......k}, and let p be a minimum weight path from amongst them. The Floyd-Warshall algorithm exploits a link between path p and shortest paths from i to j with all intermediate vertices in the set {1, 2.......k-1}. The link depends on whether or not k is an intermediate vertex of path p.
If k is not an intermediate vertex of path p, then all intermediate vertices of path p are in the set {1, 2........k-1}. Thus, the shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2.......k-1} is also the shortest path i to j with all intermediate vertices in the set {1, 2.......k}.
If k is an intermediate vertex of path p, then we break p down into i → k → j.
Let dij(k) be the weight of the shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2.......k}.
FLOYD - WARSHALL (W)
1. n ← rows [W].
2. D0 ← W
3. for k ← 1 to n
4. do for i ← 1 to n
5. do for j ← 1 to n
6. do dij(k) ← min (dij(k-1),dik(k-1)+dkj(k-1) )
7. return D(n) The strategy adopted by the Floyd-Warshall algorithm is Dynamic Programming. The running time of the Floyd-Warshall algorithm is determined by the triply nested for loops of lines 3-6. Each execution of line 6 takes O (1) time. The algorithm thus runs in time θ(n3 ).
Principle of optimality :
If k is the node on the shortest path from i to j, then the path from i to k and k to j, must also be shortest.
In the following figure, the optimal path from i to j is either p or summation of p1 and p2.
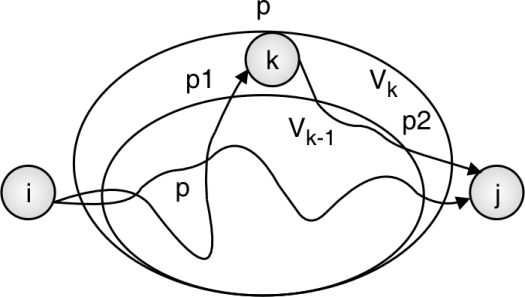
While considering kth vertex as intermediate vertex, there are two possibilities :
- If k is not part of shortest path from i to j, we keep the distance D[i, j] as it is.
- If k is part of shortest path from i to j, update distance D[i, j] as
D[i, k] + D[k, j].
Optimal sub structure of the problem is given as :
Dk [i, j] = min{ Dk – 1 [i, j], Dk – 1 [i, k] + Dk – 1 [k, j] }
Dk = Distance matrix after kth iteration
Example:
Problem: Apply Floyd’s method to find the shortest path for the below-mentioned all pairs.

Solution:
Optimal substructure formula for Floyd’s algorithm,
Dk [i, j] = min { Dk – 1 [i, j], Dk – 1 [i, k] + Dk – 1 [k, j] }
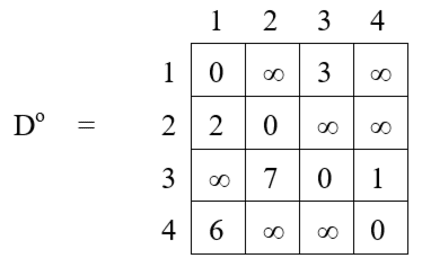
Iteration 1 : k = 1 :
D1[1, 2] = min { Do [1, 2], Do [1, 1] + Do [1, 2] }
= min {∞, 0 + ∞}
= ∞
D1[1, 3] = min { Do [1, 3], Do [1, 1] + Do [1, 3] }
= min {3, 0 + 3}
= 3
D1[1, 4] = min { Do [1, 4], Do [1, 1] + Do [1, 4] }
= min {∞, 0 + ∞}
= ∞
D1[2, 1] = min { Do [2, 1], Do [2, 1] + Do [1, 1] }
= min {2, 2 + 0}
= 2
D1[2, 3] = min { Do [2, 3], Do [2, 1] + Do [1, 3] }
= min {∞, 2 + 3}
= 5
D1[2, 4] = min { Do [2, 4], Do [2, 1] + Do [1, 4] }
= min {∞, 2 + ∞}
= ∞
D1[3, 1] = min { Do [3, 1], Do [3, 1] + Do [1, 1] }
= min {∞, 0 + ∞}
= ∞
D1[3, 2] = min { Do [3, 2], Do [3, 1] + Do [1, 2] }
= min {7, ∞ + ∞}
= 7
D1[3, 4] = min { Do [3, 4], Do [3, 1] + Do [1, 4] }
= min {1, ∞ + ∞}
= 1
D1[4, 1] = min { Do [4, 1], Do [4, 1] + Do [1, 1] }
= min {6, 6 + 0}
= 6
D1[4, 2] = min { Do [4, 2], Do [4, 1] + Do [1, 2] }
= min {∞, 6 + ∞}
= ∞
D1[4, 3] = min { Do [4, 3], Do [4, 1] + Do [1, 3] }
= min {∞, 6 + 3}
= 9
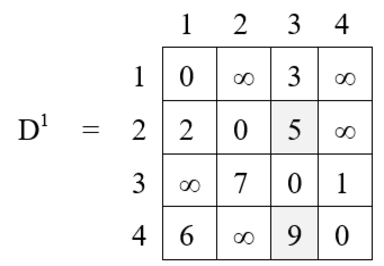
Note : Path distance for highlighted cell is improvement over original matrix.
Iteration 2 (k = 2) :
D2[1, 2] = D1 [1, 2] = ∞
D2[1, 3] = min { D1 [1, 3], D1 [1, 2] + D1 [2, 3] }
= min {3, ∞ + 5}
= 3
D2[1, 4] = min { D1 [1, 4], D1 [1, 2] + D1 [2, 4] }
= min {∞, ∞ + ∞}
= ∞
D2[2, 1] = D1 [2, 1] = 2
D2[2, 3] = D1 [2, 3] = 5
D2[2, 4] = D1 [2, 4] = ∞
D2[3, 1] = min { D1 [3, 1], D1 [3, 2] + D1 [2, 1] }
= min {∞, 7 + 2}
= 9
D2[3, 2] = D1 [3, 2] = 7
D2[3, 4] = min { D1 [3, 4], D1 [3, 2] + D1 [2, 4] }
= min {1, 7 + ∞}
= 1
D2[4, 1] = min { D1 [4, 1], D1 [4, 2] + D1 [2, 1] }
= min {6, ∞ + 2}
= 6
D2[4, 2] = D1 [4, 2] = ∞
D2[4, 3] = min { D1 [4, 3], D1 [4, 2] + D1 [2, 3] }
= min {9, ∞ + 5}
= 9
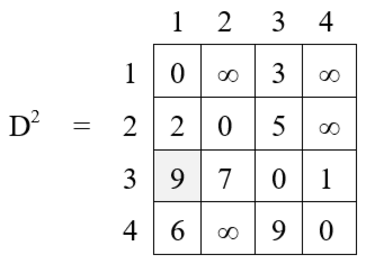
Iteration 3 (k = 3) :
D3[1, 2] = min { D2 [1, 2], D2 [1, 3] + D2 [3, 2] }
= min {∞, 3 + 7}
= 10
D3[1, 3] = D2 [1, 3] = 3
D3[1, 4] = min { D2 [1, 4], D2 [1, 3] + D2 [3, 4] }
= min {∞, 3 + 1}
= 4
D3[2, 1] = min { D2 [2, 1], D2 [2, 3] + D2 [3, 1] }
= min {2, 5 + 9}
= 2
D3[2, 3] = D2 [2, 3] = 5
D3[2, 4] = min { D2 [2, 4], D2 [2, 3] + D2 [3, 4] }
= min {∞, 5 + 1}
= 6
D3[3, 1] = D2 [3, 1] = 9
D3[3, 2] = D2 [3, 2] = 7
D3[3, 4] = D2 [3, 4] = 1
D3[4, 1] = min { D2 [4, 1], D2 [4, 3] + D2 [3, 1] }
= min {6, 9 + 9}
= 6
D3[4, 2] = min { D2 [4, 1], D2 [4, 3] + D2 [3, 2] }
= min {∞, 9 + 7}
= 16
D3[4, 3] = D2 [4, 3] = 9
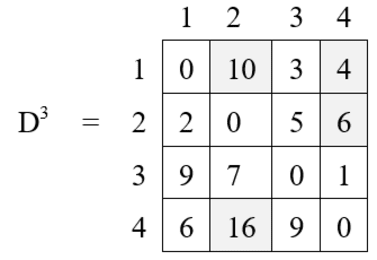
Iteration 4 (k = 4) :
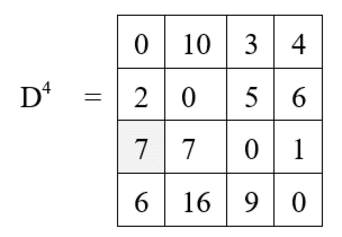
D4[1, 2] = min { D3 [1, 2], D3 [1, 4] + D3 [4, 2] }
= min {10, 4 + 16}
= 10
D4[1, 3] = min { D3 [1, 3], D3 [1, 4] + D3 [4, 1] }
= min {3, 4 + 9}
= 3
D4[1, 4] = D3 [1, 4] = 4
D4[2, 1] = min { D3 [2, 1], D3 [2, 4] + D3 [4, 1] }
= min {2, 6 + 6}
= 2
D4[2, 3] = min { D3 [2, 3], D3 [2, 4] + D3 [4, 3] }
= min {5, 6 + 9}
= 5
D4[2, 4] = D3 [2, 4] = 6
D4[3, 1] = min { D3 [3, 1], D3 [3, 4] + D3 [4, 1] }
= min {9, 1 + 6}
= 7
D4[3, 2] = min { D3 [3, 2], D3 [3, 4] + D3 [4, 2] }
= min {7, 1 + 16}
= 7
D4[3, 4] = D3 [3, 4] = 1
D4[4, 1] = D3 [4, 1] = 6
D4[4, 2] = D3 [4, 2] = 16
D4[4, 3] = D3 [4, 3] = 9
Final distance matrix is,
Problem: Obtain all pair shortest path using Floyd’s Algorithm for given weighted graph
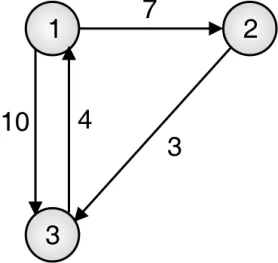
Solution:
Optimal substructure formula for Floyd’s algorithm,
Dk [i,j] = min{ Dk – 1 [i, j], Dk – 1 [i, k] + Dk – 1 [k, j] }
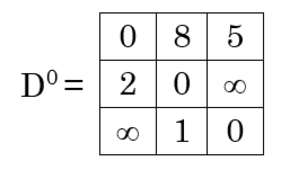
Iteration 1 (k = 1) :
D1 [1, 2] = min {D0[1, 2], D0[1, 1] + D0[1, 2] }
= min {8, 0 + 8}
= 8
D1[1, 3] = min {D0[1, 3], D0[1, 1] + D0[1, 3] }
= min {5, 0 + 5}
= 5
D1[2, 1] = min {D0[2, 1], D0[2, 1] + D0[1, 1] }
= min {2, 2 + 0}
= 2
D1[2, 3] = min {D0[2, 3], D0[2, 1] + D0[1, 3] }
= min {∞, 2 + 5}
= 7
D1[3, 1] = min {D0[3, 1], D0[3, 1] + D0[1, 1] }
= min {∞, ∞ + 0}
= ∞
D1[3, 2] = min {D0[3, 2], D0[3, 1] + D0[1, 2] }
= min {1, 1 + 8}
= 1
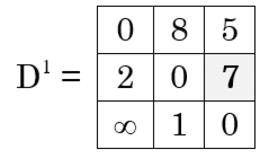
Iteration 2 (k = 2) :
D2[1, 2] = min {D1[1, 2], D1[1, 2] + D1[2, 2]}
= min {8, 8 + 0}
= 8
D2[1, 3] = min {D1[1, 3], D1[1, 2] + D1[2, 3] }
= min {5, 8 +7}
= 5
D2[2, 1] = min {D1[2, 1], D1[2, 2] + D1[2, 1}
= min {2, 0 + 2}
= 2
D2[2, 3] = min {D1[2, 3], D1[2, 2] + D1[2, 3] }
= min {7, 0 + 7}
= 7
D2[3, 1] = min {D1[3, 1], D1[3, 2] + D1[2, 1] }
= min {∞, 1 + 2}
= 3
D2[3, 2] = min {D1[3, 2], D1[3, 2] + D1[2, 2] }
= min {1, 1 + 0}
= 1
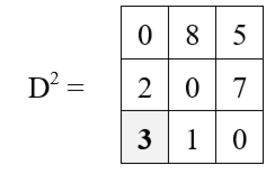
Iteration 3 (k = 3) :
D3[1, 2] = min {D2[1, 2], D2[1, 3] + D2[3, 2]}
= min {8, 5 + 1}
= 6
D3[1, 3] = min {D2[1, 3], D2[1, 3] + D2[3, 3] }
= min {5, 5 + 0}
= 5
D3[2, 1] = min {D2[2, 1], D2[2, 3] + D2[3, 1}
= min {2, 7 + 3}
= 2
D3[2, 3] = min {D2[2, 3], D2[2, 3] + D2[3, 3] }
= min {7, 7 + 0}
= 7
D3[3, 1] = min {D2[3, 1], D2[3, 3] + D2[3, 1] }
= min {3, 0 + 3}
= 3
D3[3, 2] = min {D2[3, 2], D2[3, 3] + D2[3, 2] }
= min {1, 0 + 1}
= 1
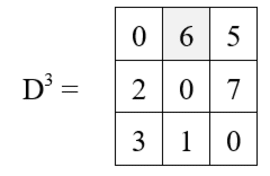





No comments:
Post a Comment