Dijkstra's Algorithm

It is a greedy algorithm that solves the single-source shortest path problem for a directed graph G = (V, E) with nonnegative edge weights, i.e., w (u, v) ≥ 0 for each edge (u, v) ∈ E.

Dijkstra's Algorithm maintains a set S of vertices whose final shortest - path weights from the source s have already been determined. That's for all vertices v ∈ S; we have d [v] = δ (s, v). The algorithm repeatedly selects the vertex u ∈ V - S with the minimum shortest - path estimate, insert u into S and relaxes all edges leaving u.

Because it always chooses the "lightest" or "closest" vertex in V - S to insert into set S, it is called as the greedy strategy.

Analysis: The running time of Dijkstra's algorithm on a graph with edges E and vertices V can be expressed as a function of |E| and |V| using the Big - O notation. The simplest implementation of the Dijkstra's algorithm stores vertices of set Q in an ordinary linked list or array, and operation Extract - Min (Q) is simply a linear search through all vertices in Q. In this case, the running time is O (|V² |+|E|=O(V² ).

Here is an example of Dijkstra's Algorithm

Let's consider the directed graph.

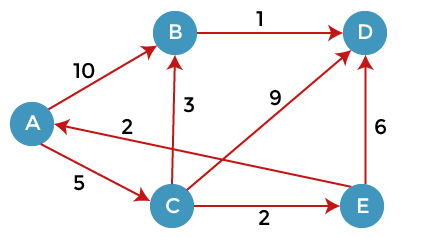
Here, we consider A as a source vertex. A vertex is a source vertex so entry is filled with 0 while other vertices filled with ∞. The distance from source vertex to source vertex is 0, and the distance from the source vertex to other vertices is ∞.

We will solve this problem using the below table:

A	B	C	D	E
∞	∞	∞	∞	∞

Since 0 is the minimum value in the above table, so we select vertex A and added in the second row shown as below:

	A	B	C	D	E
A	0	∞	∞	∞	∞

As we can observe in the above graph that there are two vertices directly connected to the vertex A, i.e., B and C. The vertex A is not directly connected to the vertex E, i.e., the edge is from E to A. Here we can calculate the two distances, i.e., from A to B and A to C. The same formula will be used as in the previous problem.

If(d(x) + c(x, y)  < d(y))  

  Then we update d(y) = d(x) + c(x, y)   

 

	A	B	C	D	E
A	0	∞	∞	∞	∞
		10	5	∞	∞

As we can observe in the third row that 5 is the lowest value so vertex C will be added in the third row.

We have calculated the distance of vertices B and C from A. Now we will compare the vertices to find the vertex with the lowest value. Since the vertex C has the minimum value, i.e., 5 so vertex C will be selected.

Since the vertex C is selected, so we consider all the direct paths from the vertex C. The direct paths from the vertex C are C to B, C to D, and C to E.

First, we consider the vertex B. We calculate the distance from C to B. Consider vertex C as 'x' and vertex B as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (5 + 3) < ∞

= 8 < ∞

Since 8 is less than the infinity so we update d(B) from ∞ to 8. Now the new row will be inserted in which value 8 will be added under the B column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
		10	5	∞	∞
		8

We consider the vertex D. We calculate the distance from C to D. Consider vertex C as 'x' and vertex D as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (5 + 9) < ∞

= 14 < ∞

Since 14 is less than the infinity so we update d(D) from ∞ to 14. The value 14 will be added under the D column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
		8		14

We consider the vertex E. We calculate the distance from C to E. Consider vertex C as 'x' and vertex E as 'y'.

d(x, y) = d(x) + c(x, y) < d(y)

= (5 + 2) < ∞

= 7 < ∞

Since 14 is less than the infinity so we update d(D) from ∞ to 14. The value 14 will be added under the D column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
		8		14	7

As we can observe in the above table that 7 is the minimum value among 8, 14, and 7. Therefore, the vertex E is added on the left as shown in the below table:

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
E		8		14	7

The vertex E is selected so we consider all the direct paths from the vertex E. The direct paths from the vertex E are E to A and E to D. Since the vertex A is selected, so we will not consider the path from E to A.

Consider the path from E to D.

d(x, y) = d(x) + c(x, y) < d(y)

= (7 + 6) < 14

= 13 < 14

Since 13 is less than the infinity so we update d(D) from ∞ to 13. The value 13 will be added under the D column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
E		8		14	7
B		8		13

The value 8 is minimum among 8 and 13. Therefore, vertex B is selected. The direct path from B is B to D.

d(x, y) = d(x) + c(x, y) < d(y)

= (8 + 1) < 13

= 9 < 13

Since 9 is less than 13 so we update d(D) from 13 to 9. The value 9 will be added under the D column.

	A	B	C	D	E
A	0	∞	∞	∞	∞
C		10	5	∞	∞
E		8		14	7
B		8		13
D				9

Disadvantage of Dijkstra's Algorithm:

1. It does a blind search, so wastes a lot of time while processing.
2. It can't handle negative edges.
3. It leads to the acyclic graph and most often cannot obtain the right shortest path.
4. We need to keep track of vertices that have been visited.