Greedy Algorithm Introduction

What Is Greedy Algorithm?

A Greedy algorithm is an approach to solving a problem that selects the most appropriate option based on the current situation. This algorithm ignores the fact that the current best result may not bring about the overall optimal result. Even if the initial decision was incorrect, the algorithm never reverses it.

This simple, intuitive algorithm can be applied to solve any optimization problem which requires the maximum or minimum optimum result. The best thing about this algorithm is that it is easy to understand and implement.

The runtime complexity associated with a greedy solution is pretty reasonable. However, you can implement a greedy solution only if the problem statement follows two properties mentioned below: 

• Greedy Choice Property: Choosing the best option at each phase can lead to a global (overall) optimal solution.
• Optimal Substructure: If an optimal solution to the complete problem contains the optimal solutions to the subproblems, the problem has an optimal substructure.

Moving forward, we will learn how to create a greedy solution for a problem that adheres to the principles listed above.

Steps for Creating a Greedy Algorithm

By following the steps given below, you will be able to formulate a greedy solution for the given problem statement:

• Step 1: In a given problem, find the best substructure or subproblem.
• Step 2: Determine what the solution will include (e.g., largest sum, shortest path).
• Step 3: Create an iterative process for going over all subproblems and creating an optimum solution.

Let’s take up a real-world problem and formulate a greedy solution for it. 

Problem: Alex is a very busy person. He has set aside time T to accomplish some interesting tasks. He wants to do as many tasks as possible in this allotted time T. For that, he has created an array A of timestamps to complete a list of items on his itinerary. 

Now, here we need to figure out how many things Alex can complete in the T time he has.

Approach to Build a Solution: This given problem is a straightforward greedy problem. In each iteration, we will have to pick the items from array A that will take the least amount of time to accomplish a task while keeping two variables in mind: current_Time and number_Of_Things. To generate a solution, we will have to carry out the following steps.

• Sort the array A in ascending order.
• Select one timestamp at a time.
• After picking up the timestamp, add the timestamp value to current_Time.
• Increase number_Of_Things by one.
• Repeat steps 2 to 4 until the current_Time value reaches T.

Example of Greedy Algorithm

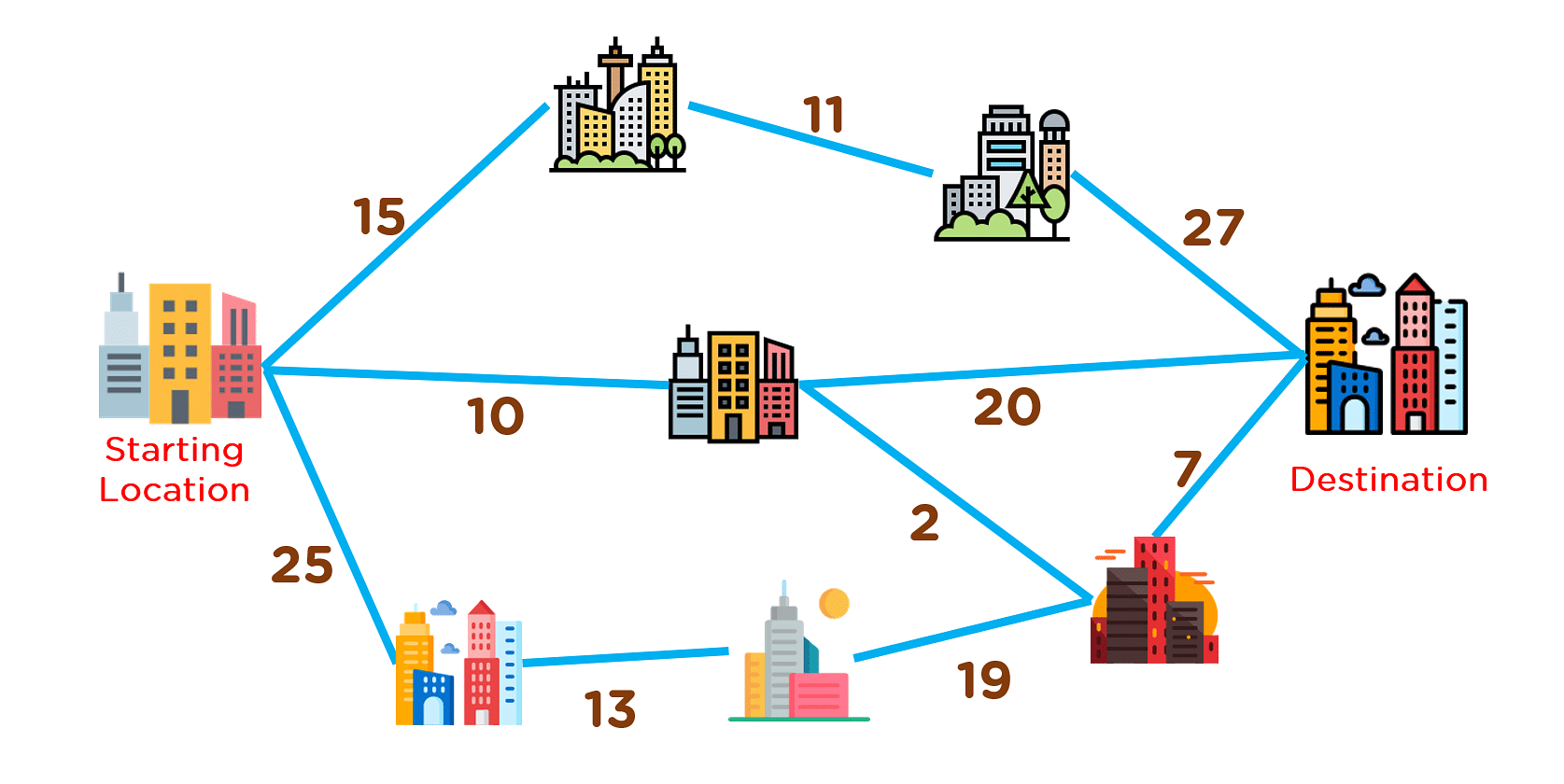
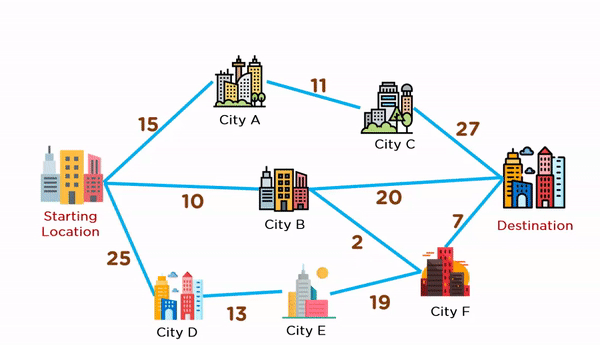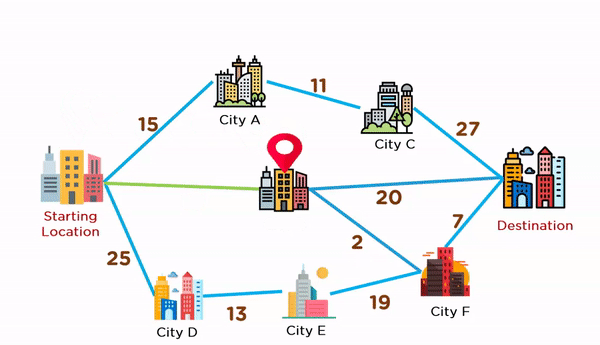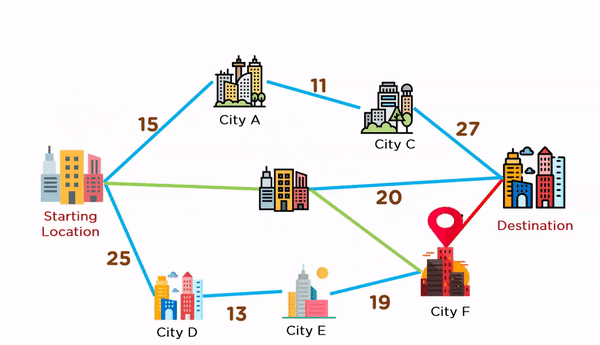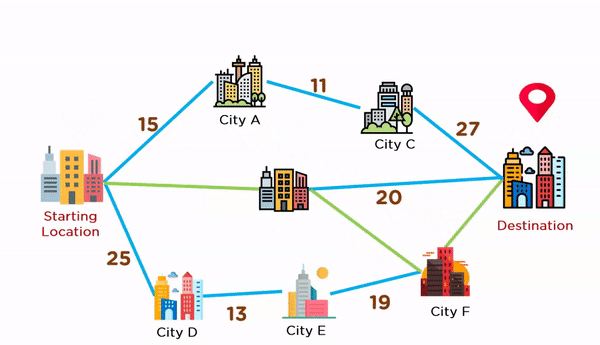
Problem Statement:  Find the best route to reach the destination city from the given starting point using a greedy method.

Greedy Solution: In order to tackle this problem, we need to maintain a graph structure. And for that graph structure, we'll have to create a tree structure, which will serve as the answer to this problem. The steps to generate this solution are given below:

• Start from the source vertex.
• Pick one vertex at a time with a minimum edge weight (distance) from the source vertex.
• Add the selected vertex to a tree structure if the connecting edge does not form a cycle.
• Keep adding adjacent fringe vertices to the tree until you reach the destination vertex.

The animation given below explains how paths will be picked up in order to reach the destination city.

Limitations of Greedy Algorithm

Factors listed below are the limitations of a greedy algorithm:

1. The greedy algorithm makes judgments based on the information at each iteration without considering the broader problem; hence it does not produce the best answer for every problem.
2. The problematic part for a greedy algorithm is analyzing its accuracy. Even with the proper solution, it is difficult to demonstrate why it is accurate. 
3. Optimization problems (Dijkstra’s Algorithm) with negative graph edges cannot be solved using a greedy algorithm.

Moving forward, let’s look at some applications of a greedy algorithm.

Applications of Greedy Algorithm

Following are few applications of the greedy algorithm:

• Used for Constructing Minimum Spanning Trees: Prim’s and Kruskal’s Algorithms used to construct minimum spanning trees are greedy algorithms.
• Used to Implement Huffman Encoding: A greedy algorithm is utilized to build a Huffman tree that compresses a given image, spreadsheet, or video into a lossless compressed file.
• Used to Solve Optimization Problems: Graph - Map Coloring, Graph - Vertex Cover, Knapsack Problem, Job Scheduling Problem, and activity selection problem are classic optimization problems solved using a greedy algorithmic paradigm.
  

Characteristics of a Greedy Method

The greedy method is a simple and straightforward way to solve optimization problems. It involves making the locally optimal choice at each stage with the hope of finding the global optimum. The main advantage of the greedy method is that it is easy to implement and understand. However, it is not always guaranteed to find the best solution and can be quite slow.

The greedy method works by making the locally optimal choice at each stage in the hope of finding the global optimum. This can be done by either minimizing or maximizing the objective function at each step. The main advantage of the greedy method is that it is relatively easy to implement and understand. However, there are some disadvantages to using this method. First, the greedy method is not guaranteed to find the best solution. Second, it can be quite slow. Finally, it is often difficult to prove that the greedy method will indeed find the global optimum.

One of the most famous examples of the greedy method is the knapsack problem. In this problem, we are given a set of items, each with a weight and a value. We want to find the subset of items that maximizes the value while minimizing the weight. The greedy method would simply take the item with the highest value at each step. However, this might not be the best solution. For example, consider the following set of items:

Item 1: Weight = 2, Value = 6

Item 2: Weight = 2, Value = 3

Item 3: Weight = 4, Value = 5

The greedy method would take Item 1 and Item 3, for a total value of 11. However, the optimal solution would be to take Item 2 and Item 3, for a total value of 8. Thus, the greedy method does not always find the best solution.

There are many other examples of the greedy method. The most famous one is probably the Huffman coding algorithm, which is used to compress data. In this algorithm, we are given a set of symbols, each with a weight. We want to find the subset of symbols that minimizes the average length of the code. The greedy method would simply take the symbol with the lowest weight at each step. However, this might not be the best solution. For example, consider the following set of symbols:

Symbol 1: Weight = 2, Code = 00

Symbol 2: Weight = 3, Code = 010

Symbol 3: Weight = 4, Code =011

The greedy method would take Symbol 1 and Symbol 3, for a total weight of 6. However, the optimal solution would be to take Symbol 2 and Symbol 3, for a total weight of 7. Thus, the greedy method does not always find the best solution.

The greedy method is a simple and straightforward way to solve optimization problems. However, it is not always guaranteed to find the best solution and can be quite slow. When using the greedy method, it is important to keep these disadvantages in mind.

Components of a Greedy Algorithm

There are four key components to any greedy algorithm:

1. A set of candidate solutions (typically represented as a graph)
2. A way of ranking the candidates according to some criteria
3. A selection function that picks the best candidate from the set, according to the ranking
4. A way of "pruning" the set of candidates, so that it doesn't contain any solutions that are worse than the one already chosen.

The first two components are straightforward - the candidate solutions can be anything, and the ranking criteria can be anything as well. The selection function is usually just a matter of picking the candidate with the highest ranking.

The pruning step is important, because it ensures that the algorithm doesn't waste time considering candidates that are already known to be worse than the best one found so far. Without this step, the algorithm would essentially be doing a brute-force search of the entire solution space, which would be very inefficient.

Disadvantages of Using Greedy Algorithms

The main disadvantage of using a greedy algorithm is that it may not find the optimal solution to a problem. In other words, it may not produce the best possible outcome. Additionally, greedy algorithms can be very sensitive to changes in input data — even a small change can cause the algorithm to produce a completely different result. Finally, greedy algorithms can be difficult to implement and understand.