The function f is called the identity function if each element of set A has an image on itself i.e. f (a) = a ∀ a ∈ A.
It is denoted by I.
Example:
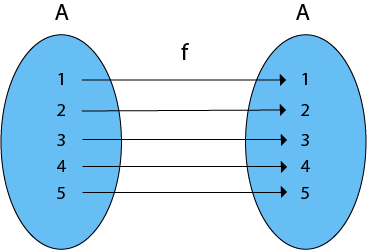
Consider, A = {1, 2, 3, 4, 5} and f: A → A such that
f = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}.
The function f is an identity function as each element of A is mapped onto itself. The function f is a one-one and onto
Invertible (Inverse) Functions
A function f: X → Y is invertible if and only if it is a bijective function.
Consider the bijective (one to one onto) function f: X → Y. As f is a one to one, therefore, each element of X corresponds to a distinct element of Y. As f is onto, there is no element of Y which is not the image of any element of X, i.e., range = co-domain Y.
The inverse function for f exists if f-1 is a function from Y to X.
Example:
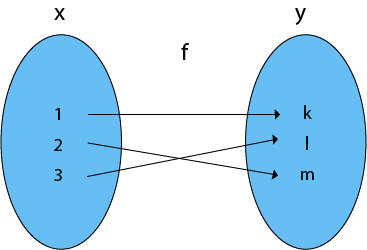
Consider, X = {1, 2, 3}
Y = {k, l, m} and f: X→Y such that
f = {(1, k), (2, m), (3, l)
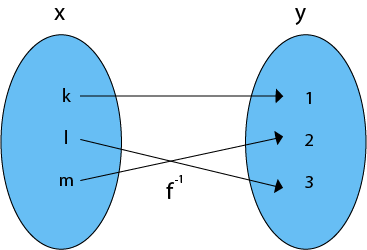
The inverse function of f is shown in fig:
0 Comments