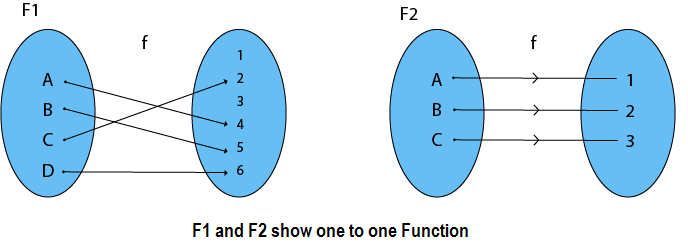
1. Injective (One-to-One) Functions: A function in which one element of Domain Set is connected to one element of Co-Domain Set.
2. Surjective (Onto) Functions: A function in which every element of Co-Domain Set has one pre-image.
Example: Consider, A = {1, 2, 3, 4}, B = {a, b, c} and f = {(1, b), (2, a), (3, c), (4, c)}.
It is a Surjective Function, as every element of B is the image of some A
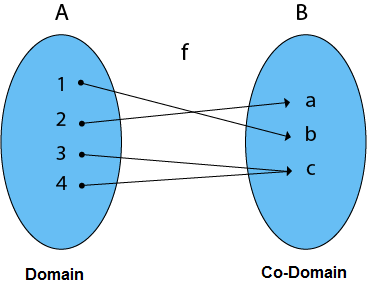
Note: In an Onto Function, Range is equal to Co-Domain.
3. Bijective (One-to-One Onto) Functions: A function which is both injective (one to - one) and surjective (onto) is called bijective (One-to-One Onto) Function.
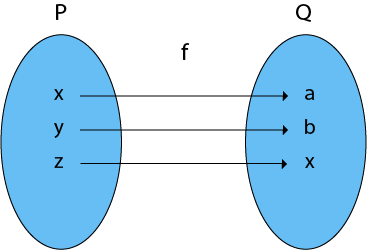
Example:
Consider P = {x, y, z}
Q = {a, b, c}
and f: P → Q such that
f = {(x, a), (y, b), (z, c)}
The f is a one-to-one function and also it is onto. So it is a bijective function.
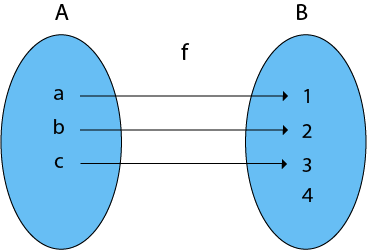
4. Into Functions: A function in which there must be an element of co-domain Y does not have a pre-image in domain X.
Example:
Consider, A = {a, b, c}
B = {1, 2, 3, 4} and f: A → B such that
f = {(a, 1), (b, 2), (c, 3)}
In the function f, the range i.e., {1, 2, 3} ≠ co-domain of Y i.e., {1, 2, 3, 4}
Therefore, it is an into function
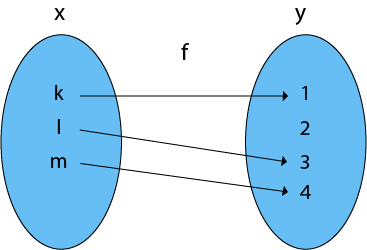
5. One-One Into Functions: Let f: X → Y. The function f is called one-one into function if different elements of X have different unique images of Y.
Example:
Consider, X = {k, l, m}
Y = {1, 2, 3, 4} and f: X → Y such that
f = {(k, 1), (l, 3), (m, 4)}
The function f is a one-one into function
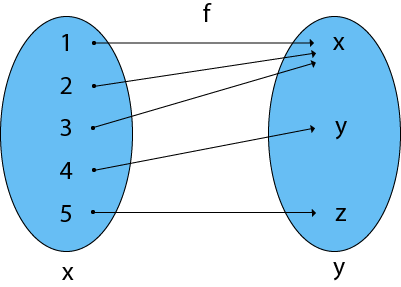
6. Many-One Functions: Let f: X → Y. The function f is said to be many-one functions if there exist two or more than two different elements in X having the same image in Y.
Example:
Consider X = {1, 2, 3, 4, 5}
Y = {x, y, z} and f: X → Y such that
f = {(1, x), (2, x), (3, x), (4, y), (5, z)}
The function f is a many-one function
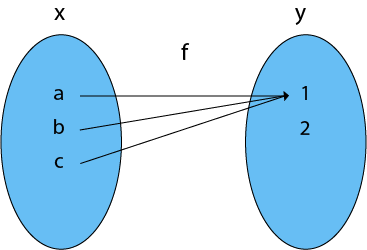
7. Many-One Into Functions: Let f: X → Y. The function f is called the many-one function if and only if is both many one and into function.
Example:
Consider X = {a, b, c}
Y = {1, 2} and f: X → Y such that
f = {(a, 1), (b, 1), (c, 1)}
As the function f is a many-one and into, so it is a many-one into function.
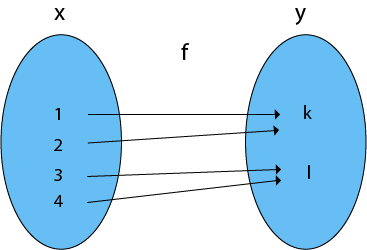
8. Many-One Onto Functions: Let f: X → Y. The function f is called many-one onto function if and only if is both many one and onto.
Example:
Consider X = {1, 2, 3, 4}
Y = {k, l} and f: X → Y such that
f = {(1, k), (2, k), (3, l), (4, l)}
The function f is a many-one (as the two elements have the same image in Y) and it is onto (as every element of Y is the image of some element X). So, it is many-one onto function



No comments:
Post a Comment