Inorder Traversal

Here, we will see how to traverse the node in an inorder fashion in a Binary search tree. In a binary search tree, the left subtree consists of nodes having a smaller value than the root node, while the right subtree consists of nodes having a greater value than the root node.

If we want to traverse the nodes in ascending order, then we use the inorder traversal. The following are the steps required for the inorder traversal:

• Visit all the nodes in the left subtree
• Visit the root node
• Visit all the nodes in the right subtree

There are two approaches used for the inorder traversal:

• Inorder traversal using Recursion
• Inorder traversal using an Iterative method

Inorder Traversal using Recursion

First, we look at the inorder traversal using recursion. Recursion means the function calls itself. In order to access each node, we first need to define the structure of the node.

struct BinaryTreeNode  
{  
     int info;  
     struct BinaryTreeNode *left;  
     struct BinaryTreeNode *right;  
}  

The above code defines the structure of the node. The name of the structure is BinaryTreeNode that contains three fields, i.e., info, left pointer, and right pointer. The info field contains the value of the node, the left pointer contains the address of the left node, and the right pointer contains the address of the right node.

Recursive approach of Inorder traversal

void inorder_traversal(struct BinaryTreeNode *root)  
{  
    if(root)  
{  
    inorder_traversal(root->left);  
    printf("%d", root->info);  
    inorder_traversal(root->right);  
}  
}  

The above approach is the recursive approach. Inside the parenthesis of inorder_traversal function, we have passed the root pointer of type struct BinaryTreeNode, which is pointing to the root node of the tree. First, we will check whether the root is NULL or not. If the root is null means that the tree is empty. If the root is not empty, then the inorder_traversal(root_left) function will be called recursively to print all the left subtree nodes and then the root node. Once the left subtree is traversed, and the root node, the inorder_traversal(root_right) will be called recursively to print all the right subtree nodes.

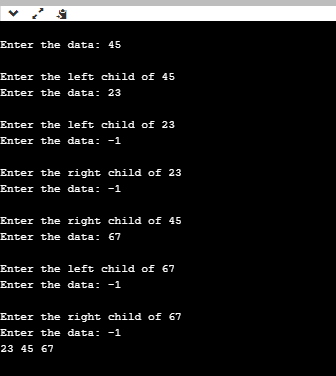
Implementation of Inorder traversal in C.

1. #include<stdio.h>    
2. // Creating a node structure  
3.       struct BinaryTreeNode    
4.      {    
5.           int info;    
6.           struct BinaryTreeNode *left;  
7.           struct BinaryTreeNode *right;    
8.       };  
9.     
10.   // Creating a tree..    
11. struct BinaryTreeNode* create()    
12. {    
13.    struct BinaryTreeNode *temp;    
14.    int data;    
15.   temp = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));  // creating a new node  
16.    printf("\nEnter the data: ");    
17.    scanf("%d", &data);     
18.      
19.    if(data==-1)    
20. {    
21. return NULL;    
22. }    
23.   temp->info = data;    
24.    printf("\nEnter the left child of %d", data);    
25.    temp->left = create();  // creating a left child  
26. printf("\nEnter the right child of %d", data);    
27. temp->right = create();  // creating a right child  
28. return temp;     
29.  }  
30.    
31.  //inorder traversal  
32. void inorder(struct BinaryTreeNode *root)  
33. {  
34.     if(root==NULL)  
35.     return;  
36.     else  
37.       
38.     inorder(root->left);  
39.     printf("%d ", root->info);  
40.     inorder(root->right);  
41. }  
42.   void main()    
43.     {    
44.        struct BinaryTreeNode *root;    
45.        root = create();  // calling create function.  
46.        inorder(root);   // calling inorder function  
47.     }  

Output

Iterative Inorder Traversal

The second approach is the iterative approach for the inorder traversal. When we were using the recursive approach, we used the system stack for the inorder traversal. For the iterative approach, we will use the external stack. Let's understand through an example.

Consider the below tree:

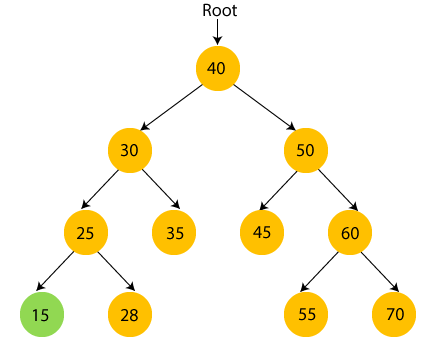
Now we have to perform the inorder traversal using an external stack. The following are the steps required to perform the inorder traversal:

Step 1: First we push the root node, i.e., 10, into the stack:

Stack: 10

Step 2: Node 10 has a left child, i.e., 11, so we will push node 11 into the stack.

Stack: 10, 11

Step 3: Node 11 has a left child, i.e., 2, so we will push element 2 into the stack.

Stack: 10, 11, 2

Step 4: Since node 2 does not have a left child, we will pop node 2 from the stack and get printed in the output. Set the root node as NULL.

Stack: 10, 11

Output: 2

Step 5: Since the root node is NULL, so pop node 11 from the stack.

Stack: 10

Output: 2, 11

Step 6: Node 11 has a right child, i.e., -1, so set the root as -1. Push -1 into the stack.

Stack: 10, -1

Step 7: Since node -1 does not have a left or a right child, so set the root as NULL. Pop -1 from the stack.

Stack: 10

Output: 2, 11, -1

Step 8: Since the root is NULL, pop 10 from the stack. Node 10 has a right child, i.e., 16, so set root to 16.

Stack: empty

Output: 2, 11, -1, 10

Step 9: The root is 16, so push 16 into the stack.

Stack: 16

Step 10: Node 16 has also left child, i.e., 10, so push 10 into the stack. Set root to 10.

Stack: 16, 10.

Step 11: The node 10 has a left child, i.e., 9, so push 9 into the stack. Set root to 9.

Stack: 16, 10, 9

Step 12: Since the node 9 has no left and right child so set root as NULL. Pop element 9 from the stack.

Stack: 16, 10

Output: 2, 11, -1, 10, 9

Step 13: The root is set to node 9 and the topmost element is 10, so pop element 10 from the stack. The node 10 has a right child, i.e., node 11. Set root to node 11.

Stack: 16

Output: 2, 11, -1, 10, 9, 10

Step 14: The root is set to 11 so push element 11 into the stack.

Stack: 16, 11

Step 14: Since the root is set to 11 and it does not have any left and right child, pop element 11 from the stack. Set root to NULL.

Stack: 16

Output: 2, 11, -1, 10, 9, 10, 11

Step 15: The root is set to NULL, so pop element 16 from the stack. Since the node 16 does not have a right child, set root node to NULL.

Stack: empty

Output: 2, 11, -1, 10, 9, 10, 11, 16

Algorithm of iterative inorder traversal

1. Step 1: Create an empty stack named as 'S'.  
2. Step 2: Initialize current node to root.  
3. Step 3: Push current node to the stack 'S' and then set current = current->left until the current node is NULL.  
4. Step 4: If current node is NULL and stack 'S' is not empty:  
5.      i) Pop topmost item of stack and print it.  
6.      ii) Set current= popped item->right  
7.      iii) Repeat step 3  
8. Step 5: If both current node and stack are empty means that the inorder traversal is completed.