Preorder Traversal

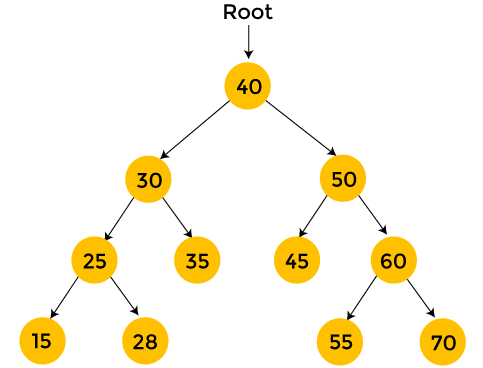
The tree which is shown below has some nodes which are completely filled with the characters. As we already know that in Depth First Traversal, if we go in one direction, then we visit all the nodes in that direction. In other words, if we go in one direction then we visit the whole subtree in that direction. After visiting all the nodes in that subtree, we move in another direction. In the above example, if we are at the root, and we move to the left subtree then we visit all the nodes in the left subtree then only we can move to the right subtree for traversal. Here, the problem is reduced in a recursive manner; therefore, we can say that visiting all the nodes of the tree is visiting the left subtree, then right subtree, and then the root node of the tree. In Depth First strategy, the relative order of visiting left subtree, right subtree, and root is different. The depth-first strategy has one constraint that the left subtree is always traversed before the right subtree.

What is a Preorder Traversal?

The preorder traversal is a traversal in which first we visit the root node, then the left subtree, and then the right subtree. It can be represented as:

<root> <left> <right>

Steps for the Preorder traversal

Step 1: First, we visit the root node.

Step 2: Secondly, we visit the left subtree.

Step 3: Lastly, we visit the right subtree.

Algorithm of Preorder traversal

Step 1: Repeat Steps 2 to 4 while TREE != NULL

Step 2: Write TREE -> DATA

Step 3: PREORDER(TREE -> LEFT)

Step 4: PREORDER(TREE -> RIGHT)
[END OF LOOP]

Step 5: END

Implementation of Binary Tree in C

1. #include<stdio.h>    
2. // Creating a node structure  
3.       struct node    
4.      {    
5.           int data;    
6.           struct node *left, *right;    
7.       };  
8.     
9.   // Creating a tree..    
10. struct node* create()    
11. {    
12.    struct node *temp;    
13.    int data;    
14.   temp = (struct node *)malloc(sizeof(struct node));  // creating a new node  
15.    printf("\nEnter the data: ");    
16.    scanf("%d", &data);     
17.      
18.    if(data==-1)    
19. {    
20. return NULL;    
21. }    
22.   temp->data = data;    
23.    printf("\nEnter the left child of %d", data);    
24.    temp->left = create();  // creating a left child  
25. printf("\nEnter the right child of %d", data);    
26. temp->right = create();  // creating a right child  
27. return temp;     
28.  }  
29.    
30.  //Preorder traversal  
31. void preorder(struct node *root)  
32. {  
33.     if(root==NULL)  
34.     return;  
35.     else  
36.     printf("%d ", root->data);  
37.     preorder(root->left);  
38.     preorder(root->right);  
39. }  
40.   void main()    
41.     {    
42.        struct node *root;    
43.        root = create();  // calling create function.  
44.        preorder(root);   // calling preorder function  
45.     }   

Explanation of the above code

In the above code, we have defined two functions, i.e., create() and preorder() function. The create() function is used to create a tree by creating a new node on every recursive call. In the preorder() function, the root node of type node structure is passed as an argument. The root node is a pointer that points to the root node of the tree. As we know that in preorder traversal, first, we visit the root node, then the left subtree, and then we traverse the right subtree. In the preorder() function, first, we print the root node, then we made a recursive call on the left subtree to print all the nodes of the left subtree and then we made a recursive call on the right subtree to print all the nodes of the right subtree.

Output