Insertion Sort Algorithm

What is Sorting in Data Structure?

Sorting is the process of arranging items in a specific order or sequence. It is a common algorithmic problem in computer science and is used in various applications such as searching, data analysis, and information retrieval.

In other words, you can say that sorting is also used to represent data in a more readable format. Some real-life examples of sorting are:-

• Contact List in Your Mobile Phone also contains all contacts arranged alphabetically (lexicographically). So if you look for contact then you don’t have to look randomly and can be searched easily and many others like Apps on your phone.
• Keywords in Your book are also in a lexicographical manner and you can find it according to Chapter.

Why Sorting is Important?

• When you perform sorting on an array/elements, many problems become easy (e.g. min/max, kth smallest/largest)
• Performing Sorting also gives no. of algorithmic solutions that contain many other ideas such as:

1. Iterative
2. Divide-and-conquer
3. Comparison vs non-comparison based
4. Recursive

The main advantage of sorting is time complexity and that’s the most important thing when you solve a problem because it’s not enough you’re able to solve a problem but you should be able to solve it in the minimum time possible. Sometimes problems can be solved easily and quickly based on sorting which can prevent you from every Coder’s Nightmare i.e. TLE (Time Limit Exceeded).

Sorting Categories

The Sorting categories in data structures can be broadly classified into the following types:

Comparison-based Sorting Algorithms: These algorithms compare the elements being sorted to each other and then place them in the desired order. Examples include Bubble Sort, Selection Sort, Insertion Sort, QuickSort, Merge Sort, and Heap Sort.

Non-Comparison-based Sorting Algorithms: These algorithms do not compare the elements being sorted to each other. Instead, they use some specific characteristics of the data to sort them. Examples include Counting Sort, Radix Sort, and Bucket Sort.

Stable Sorting Algorithms: These algorithms maintain the relative order of elements with equal keys during Sorting. Examples include Merge Sort and Insertion Sort.

Unstable Sorting Algorithms: These algorithms do not maintain the relative order of the elements with equal keys during Sorting. Examples include QuickSort and Heap Sort.

In-place Sorting and Not-in-Place Sorting

‘In place’ means whenever you are sorting and you don’t require any extra space except the input space excluding the constant space which is used for variables or iterators. It also doesn’t include the space used for stack in the recursive algorithms. Now, In merge sort, when we perform merging then the merge function requires extra linear space which is not constant. So, it is not in-place. Hence, it is called ‘out of place’ algorithm or sorting.

On the other hand, Quicksort is kind of sorting which uses only some constant number of variables for partitioning purpose. So, it is an in-place algorithm or sorting.

Stable and Not stable Sorting

• A sorting algorithm when two objects with equal keys appear in the same order in the sorted output as they appear in the unsorted input.
• Whereas a sorting algorithm is called as an unstable sorting if there are two or more objects with equal keys which don’t appear in the same order before and after sorting.
   

Above we can see an example of stable sorting here number 26 is appearing two times at respective position 6 and 8 and their occurrence is kept in unsorted and sorted array i.e. element 26 (blue) at position 6 appears first in unsorted and then appears in sorted array.

One thing should be kept in mind in the case of an unstable sort, the order of appearance/occurrence before and after sorting is not necessarily preserved.

There are some sorting algorithms which are stable by nature such as Insertion sort, Merge Sort, Bubble Sort, etc. while on the other hand sorting algorithms like Heap Sort, Quick Sort are vice-versa.

Adaptive and Non–Adaptive Sorting Algorithm

When occurrence of the elements to be sorted of an input array matters the time complexity of a sorting algorithm, then that algorithm is called “Adaptive” sorting algorithm.

For example, Insertion sort is an adaptive sorting algorithm like in the case if input is already sorted then we know that time complexity will be O(n). That’s why If the input array is almost sorted then choose insertion sort, though this is not the only thing to be kept in mind for Insertion sort over other sorting algorithms.

Merge Sort is a “Non-Adaptive” Sorting algorithm because the order of the elements in the array doesn’t matter So the time complexity of algorithm will always be O(nlogn).

Adaptive sorting algorithms:

• Bubble Sort
• Insertion Sort
• Quick Sort
   

Non-adaptive sorting algorithms:

• Selection Sort
• Merge Sort
• Heap Sort

Which sorting is best in data structures?

Every sorting algorithms have their own advantages and disadvantages. Select the sorting algorithm that is best fitted for your data. If you’re constrained in space the choose heap sort. If you need something stable choosing merge sort will help you. For almost sorted data, considering insertion sort is O(n) time!

Inbuilt sorting algorithms use hybrid sorts which are combination of different basic sorting algorithms. Introsort (std::sort in C++) which runs quick sort and switches to heap sort when the recursion gets too deep. This way, you get the fast performance of quick sort in practice while guaranteeing a worst case O(nlogn) run time.

Which sort is the fastest?

Quicksort is considered to be one of the fastest sorting algorithms. It is also considered to be the best sorting algorithm. Some of its features are that it is basically a comparison sort and can be done in-place in an array, however, inefficient implementation, it’s not a stable sort.

Though the worst-case complexity is O(n^2), on an average it gives us O(nlogn) time complexity. You can also think of considering Merge sort, which is very similar to Quicksort but has more complexity than quicksort.

Insertion sort :

Insertion sort works similar to the sorting of playing cards in hands. It is assumed that the first card is already sorted in the card game, and then we select an unsorted card. If the selected unsorted card is greater than the first card, it will be placed at the right side; otherwise, it will be placed at the left side. Similarly, all unsorted cards are taken and put in their exact place.

The same approach is applied in insertion sort. The idea behind the insertion sort is that first take one element, iterate it through the sorted array. Although it is simple to use, it is not appropriate for large data sets as the time complexity of insertion sort in the average case and worst case is O(n²), where n is the number of items. Insertion sort is less efficient than the other sorting algorithms like heap sort, quick sort, merge sort, etc.

Insertion sort has various advantages such as -

• Simple implementation
• Efficient for small data sets
• Adaptive, i.e., it is appropriate for data sets that are already substantially sorted.

Now, let's see the algorithm of insertion sort.

Algorithm

The simple steps of achieving the insertion sort are listed as follows -

Step 1 - If the element is the first element, assume that it is already sorted. Return 1.

Step2 - Pick the next element, and store it separately in a key.

Step3 - Now, compare the key with all elements in the sorted array.

Step 4 - If the element in the sorted array is smaller than the current element, then move to the next element. Else, shift greater elements in the array towards the right.

Step 5 - Insert the value.

Step 6 - Repeat until the array is sorted.

 

Working of Insertion sort Algorithm

Now, let's see the working of the insertion sort Algorithm.

array $A[]=[7,4,5,2]$.

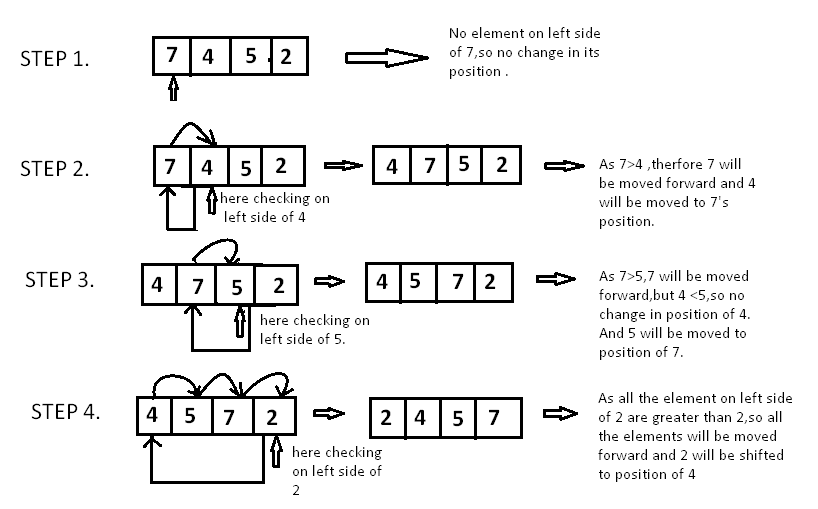
Since 7 is the first element has no other element to be compared with, it remains at its position. Now when on moving towards 4, 7 is the largest element in the sorted list and greater than 4. So, move 4 to its correct position i.e. before 7. Similarly with 5, as 7  (largest element in the sorted list) is greater than 5, we will move to its correct position. Finally for 2, all the elements on the left side of 2(sorted list) are moved one position forward as all are greater than and then 2 is placed in the first position. Finally, the given array will result in a sorted array.

Insertion sort complexity

Now, let's see the time complexity of insertion sort in best case, average case, and in worst case. We will also see the space complexity of insertion sort.

1. Time Complexity

Case	Time Complexity
Best Case	O(n)
Average Case	O(n2)
Worst Case	O(n2)

• Best Case Complexity - It occurs when there is no sorting required, i.e. the array is already sorted. The best-case time complexity of insertion sort is O(n).
• Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of insertion sort is O(n²).
• Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of insertion sort is O(n²).

2. Space Complexity

Space Complexity	O(1)
Stable	YES

• The space complexity of insertion sort is O(1). It is because, in insertion sort, an extra variable is required for swapping.

Implementation of insertion sort

Now, let's see the programs of insertion sort in different programming languages.

Program: Write a program to implement insertion sort in C language.

#include <stdio.h>  
  
void insert(int a[], int n) /* function to sort an aay with insertion sort */  
{  
    int i, j, temp;  
    for (i = 1; i < n; i++) {  
        temp = a[i];  
        j = i - 1;  
  
        while(j>=0 && temp <= a[j])  /* Move the elements greater than temp to one position ahead from their current position*/  
        {    
            a[j+1] = a[j];     
            j = j-1;    
        }    
        a[j+1] = temp;    
    }  
}  
  
void printArr(int a[], int n) /* function to print the array */  
{  
    int i;  
    for (i = 0; i < n; i++)  
        printf("%d ", a[i]);  
}  
  
int main()  
{  
    int a[] = { 12, 31, 25, 8, 32, 17 };  
    int n = sizeof(a) / sizeof(a[0]);  
    printf("Before sorting array elements are - \n");  
    printArr(a, n);  
    insert(a, n);  
    printf("\nAfter sorting array elements are - \n");    
    printArr(a, n);  
  
    return 0;  
}    

Output: