In selection sort, the smallest value among the unsorted elements of the array is selected in every pass and inserted to its appropriate position into the array. It is also the simplest algorithm. It is an in-place comparison sorting algorithm. In this algorithm, the array is divided into two parts, first is sorted part, and another one is the unsorted part. Initially, the sorted part of the array is empty, and unsorted part is the given array. Sorted part is placed at the left, while the unsorted part is placed at the right.
In selection sort, the first smallest element is selected from the unsorted array and placed at the first position. After that second smallest element is selected and placed in the second position. The process continues until the array is entirely sorted.
The average and worst-case complexity of selection sort is O(n2), where n is the number of items. Due to this, it is not suitable for large data sets.
Selection sort is generally used when -
- A small array is to be sorted
- Swapping cost doesn't matter
- It is compulsory to check all elements
Now, let's see the algorithm of selection sort.
Algorithm
Now, let's see the working of the Selection sort Algorithm.
To understand the working of the Selection sort algorithm, let's take an unsorted array. It will be easier to understand the Selection sort via an example.
Let the elements of array are -

Now, for the first position in the sorted array, the entire array is to be scanned sequentially.
At present, 12 is stored at the first position, after searching the entire array, it is found that 8 is the smallest value.
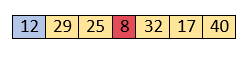
So, swap 12 with 8. After the first iteration, 8 will appear at the first position in the sorted array.

For the second position, where 29 is stored presently, we again sequentially scan the rest of the items of unsorted array. After scanning, we find that 12 is the second lowest element in the array that should be appeared at second position.

Now, swap 29 with 12. After the second iteration, 12 will appear at the second position in the sorted array. So, after two iterations, the two smallest values are placed at the beginning in a sorted way.

The same process is applied to the rest of the array elements. Now, we are showing a pictorial representation of the entire sorting process.
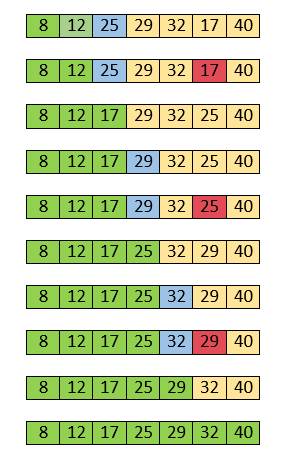
Now, the array is completely sorted.
Selection sort complexity
Now, let's see the time complexity of selection sort in best case, average case, and in worst case. We will also see the space complexity of the selection sort.
1. Time Complexity
| Case | Time Complexity |
|---|---|
| Best Case | O(n2) |
| Average Case | O(n2) |
| Worst Case | O(n2) |
- Best Case Complexity - It occurs when there is no sorting required, i.e. the array is already sorted. The best-case time complexity of selection sort is O(n2).
- Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of selection sort is O(n2).
- Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of selection sort is O(n2).
2. Space Complexity
| Space Complexity | O(1) |
| Stable | YES |
- The space complexity of selection sort is O(1). It is because, in selection sort, an extra variable is required for swapping.
Implementation of selection sort
Now, let's see the programs of selection sort in different programming languages.
Program: Write a program to implement selection sort in C language.
#include <stdio.h>
void selection(int arr[], int n)
{
int i, j, small;
for (i = 0; i < n-1; i++) // One by one move boundary of unsorted subarray
{
small = i; //minimum element in unsorted array
for (j = i+1; j < n; j++)
if (arr[j] < arr[small])
small = j;
// Swap the minimum element with the first element
int temp = arr[small];
arr[small] = arr[i];
arr[i] = temp;
}
}
void printArr(int a[], int n) /* function to print the array */
{
int i;
for (i = 0; i < n; i++)
printf("%d ", a[i]);
}
int main()
{
int a[] = { 12, 31, 25, 8, 32, 17 };
int n = sizeof(a) / sizeof(a[0]);
printf("Before sorting array elements are - \n");
printArr(a, n);
selection(a, n);
printf("\nAfter sorting array elements are - \n");
printArr(a, n);
return 0;
}
Output:
After the execution of above code, the output will be -
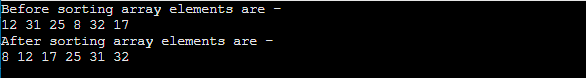





No comments:
Post a Comment