Normal SubGroup

Let G be a group. A subgroup H of G is said to be a normal subgroup of G if for all h∈ H and x∈ G, x h x^-1∈ H

If x H x^-1 = {x h x^-1| h ∈ H} then H is normal in G if and only if xH x^-1⊆H, ∀ x∈ G

Statement: If G is an abelian group, then every subgroup H of G is normal in G.

Proof: Let any h∈ H, x∈ G, then
x h x^-1= x (h x^-1)
x h x^-1= (x x^-1) h
x h x^-1 = e h
x h x^-1 = h∈ H

Hence H is normal subgroup of G.

Group Homomorphism:

A homomorphism is a mapping f: G→ G' such that f (xy) =f(x) f(y), ∀ x, y ∈ G. The mapping f preserves the group operation although the binary operations of the group G and G' are different. Above condition is called the homomorphism condition.

Kernel of Homomorphism: - The Kernel of a homomorphism f from a group G to a group G' with identity e' is the set {x∈ G | f(x) =e'}

The kernel of f is denoted by Ker f.

If f: G→G' is a homomorphism of G intoG', then the image set of f is the range, denoted by f (G), of the map f. Thus

Im (f) = f (G) = {f(x)∈ G'| x ∈G}

If f (G) =G', then G' is called a homomorphic image of G.

Note: - A group homomorphism

Isomorphism:

Let (G₁,*) and (G₂,0) be two algebraic system, where * and 0 both are binary operations. The systems (G₁,*) and (G₂,0) are said to be isomorphic if there exists an isomorphic mapping f: G₁→G₂

When two algebraic systems are isomorphic, the systems are structurally equivalent and one can be obtained from another by simply remaining the elements and operation.

Example: Let (A₁,*) and (A₂,⊡) be the two algebraic systems as shown in fig. Determine whether the two algebraic systems are isomorphic.

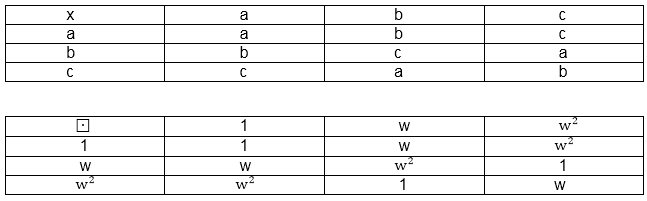
Solution: The two algebraic system (A₁,*) and (A₂,⊡) are isomorphic and (A₂,⊡) is an isomorphic image of A₁, such that

        f( a)=1
        f (b)=w
        f (c)= w²

Automorphism:

Let (G₁,*) and (G₂,0) be two algebraic system, where * and 0 both are binary operations on G₁ and G₂ respectively. Then an isomorphism from (G₁,*) to (G₂,0) is called an automorphism if G₁= G₂

Rings:

An algebraic system (R, +,) where R is a set with two arbitrary binary operations + and ., is called aring if it satisfies the following conditions

1. (R, +) is an abelian group.
2. (R,∙) is a semigroup.
3. The multiplication operation, is distributive over the addition operation +i.e.,
           a (b+c)=ab +ac and (b+c)a = ba + ca for all a, b, c ∈ R.

Example1: Consider M be the set of all matrices of the type 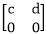 over integers under matrix addition and matrix multiplication. Thus M form a ring.

Example2: The set Z₉ = {0, 1, 2, 3, 4, 5, 6, 7, 8} under the operation addition and multiplication modulo 9 forms a ring.

Types of Rings:

1. Commutative Rings: A ring (R, +,) is called a commutative ring if it holds the commutative law under the operation of multiplication i.e., a. b = b. a, for every a, b∈ R

Example1: Consider a set E of all even integers under the operation of addition and multiplication. The set E forms a commutative ring.

2. Ring with Unity: A ring (R, +,) is called a ring with unity, if it has a multiplicative identity i.e,

Example: Consider a set M of all 2 x 2 matrices over integers under matrix multiplication and matrix addition. The set M forms a ring with unity.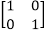

3. Ring with Zero Divisions: If a.b=0, where a and b are any two non-zero elements of R in the ring (R, +) then a and b are called divisions of zero and the ring (R, +) is called ring with zero division.

4. Rings without Zero Division: An algebraic system (R, +) where R is a set with two arbitrary binary operation + and is called a ring without divisors of zero if for every a, b ∈R, we have a.b≠0 ⟹a≠0 and b ≠0

SubRings:

A subset A of a ring (R, +) is called a subring of R, if it satisfies following conditions:

(A, +) is a subgroup of the group (R,+)

A is closed under the multiplication operation i.e., a.b ∈A,for every a,b ∈A.

Example: The ring (I, +) of integers is a subring of ring (R, +) of real numbers.

Note:
1. If R is any ring then {0} and R are subrings of R.
2. Sum of two subrings may not be a subring.
3. Intersection of subring is a subring.