Subgroups and order

If a non-void subset H of a group G is itself a group under the operation of G, we say H is a subgroup of G.

Theorem: - A subset H of a group G is a subgroup of G if:

• the identity element a∈ H.
• H is closed under the operation of G i.e. if a, b∈ H, then a, b∈ H and
• H is closed under inverses, that is if a∈ H then a^-1∈ H.

Cyclic Subgroup:-

A Subgroup K of a group G is said to be cyclic subgroup if there exists an element x∈ G such that every element of K can be written in the form xⁿ for some n ∈Z.

The element x is called generator of K and we write K= <x>

Cyclic Group:-

In the case when G=, we say G is cyclic and x is a generator of G. That is, a group G is said to be cyclic if there is an element x∈ G such that every element of G can be written in the form xⁿ for the some n∈ Z.

Example: The group G= {1, -1, i,-i} under usual multiplication is a finite cyclic group with i as generator, since i¹=i,i²=-1,i³=-i and i⁴=1

Abelian Group:

Let us consider an algebraic system (G,*), where * is a binary operation on G. Then the system (G,*) is said to be an abelian group if it satisfies all the properties of the group plus a additional following property:

(1) The operation * is commutative i.e.,
a * b = b * a ∀ a,b ∈G

Example: Consider an algebraic system (G, *), where G is the set of all non-zero real numbers and * is a binary operation defined by

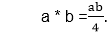
Show that (G, *) is an abelian group.

Solution:

Closure Property: The set G is closed under the operation *, since a * b = 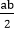 is a real number. Hence, it belongs to G.

Associative Property: The operation * is associative. Let a,b,c∈G, then we have

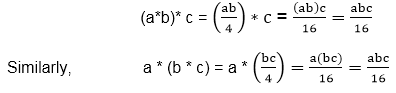
Identity: To find the identity element, let us assume that e is a +ve real number. Then e * a = a, where a ∈G.

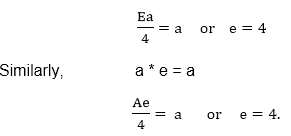
Thus, the identity element in G is 4.

Inverse: let us assume that a ∈G. If a^-1∈Q, is an inverse of a, then a * a^-1=4

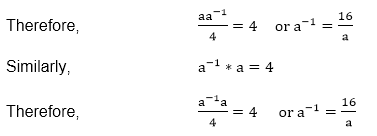
Thus, the inverse of element a in G is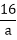

Commutative: The operation * on G is commutative.

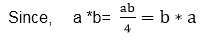
Thus, the algebraic system (G, *) is closed, associative, identity element, inverse and commutative. Hence, the system (G, *) is an abelian group.

Product of Groups:

Theorem: Prove that if (G₁,*₁)and (G₂,*₂) are groups, then G = G₁ x G₂ i.e., (G, *) is a group with operation defined by (a₁,b₁)*( a₂,b₂ )=(a₁,*₁,a₂, b₁ *₂ b₂).

Proof: To prove that G₁ x G₂ is a group, we have to show that G₁ x G₂ has the associativity operator, has an identity and also exists inverse of every element.

Associativity. Let a, b, c ∈ G₁ x G₂,then

So,        a * (b * c) = (a₁,a₂ )*((b₁,b₂)*(c₁,c₂))
                = (a₁,a₂ )*(b₁ *₁ c₁,b₂ *₂ c₂)
                = (a₁ *₁ (b₁ *₁ c₁ ),a₂ *₂ (b₂ *₂ c₂)
                = ((a₁ *₁ b₁) *₁ c₁,( a₂ *₂ b₂) *₂ c₂)
                = (a₁ *₁ b₁,a₂ *₂ b₂)*( c₁,c₂)
                = ((a₁,a₂)*( b₁,b₂))*( c₁,c₂)
                = (a * b) * c.

Identity: Let e₁ and e₂ are identities for G₁ and G₂ respectively. Then, the identity for G₁ x G₂ is e=(e₁,e₂ ).Assume same a ∈ G₁ x G₂

Then,        a * e = (a₁,a₂)*( e₁,e₂)
                = (a₁ *₁ e₁,a₂ *₂ e₂)
                = (a₁,a₂)=a

Similarly, we have e * a = a.

Inverse: To determine the inverse of an element in G₁ x G₂, we will determine it component wise i.e.,
                a^-1=(a₁,a₂)^-1=(a₁^-1,a₂^-1 )

Now to verify that this is the exact inverse, we will compute a * a^-1 and a^-1*a.

Now,         a * a^-1=(a₁,a₂ )*(a₁^-1,a₂^-1 )
                = (a₁ *₁ a₁^-1,a₂ *₂ a₂^-1)=( e₁,e₂)=e

Similarly, we have a^-1*a=e.

Thus, (G₁ x G₂,*) is a group.

In general, if G₁,G₂,....G_n are groups, then G = G₁ x G₂ x.....x G_n is also a group.

Cosets:

Let H be a subgroup of a group G. A left coset of H in G is a subset of G whose elements may be expressed as xH={ xh | h ∈ H } for any x∈ G. The element x is called a representation of the coset. Similarly, a right coset of H in G is a subset that may be expressed as Hx= {hx | h ∈H } , for any x∈G. Thus complexes xH and Hx are called respectively a left coset and a right coset.

If the group operation is additive (+) then a left coset is denoted as x + H={x+h | h ∈H} and a right coset is denoted by H + x = {h+x | h ∈ H}

 

Order of Group –

The Order of a group (G) is the number of elements present in that group, i.e it’s cardinality. It is denoted by |G|.
Order of element a ∈ G is the smallest positive integer n, such that aⁿ= e, where e denotes the identity element of the group, and aⁿ denotes the product of n copies of a. If no such n exists, a is said to have infinite order. All elements of finite groups have finite order.

Lagrange’s Theorem:

If H is a subgroup of finite group G then the order of subgroup H divides the order of group G.

Properties of the order of an element of the group:
• The order of every element of a finite group is finite.
• The Order of an element of a group is the same as that of its inverse a^-1.
• If a is an element of order n and p is prime to n, then a^p is also of order n.
• Order of any integral power of an element b cannot exceed the order of b.
• If the element a of a group G is order n, then a^k=e if and only if n is a divisor of k.
• The order of the elements a and x^-1ax is the same where a, x are any two elements of a group.
• If a and b are elements of a group then the order of ab is same as order of ba.