Sparse Matrix and its representations

A matrix is a two-dimensional data object made of m rows and n columns, therefore having total m x n values. If most of the elements of the matrix have 0 value, then it is called a sparse matrix.

Why to use Sparse Matrix instead of simple matrix ?

• Storage: There are lesser non-zero elements than zeros and thus lesser memory can be used to store only those elements.
• Computing time: Computing time can be saved by logically designing a data structure traversing only non-zero elements..

Example: 

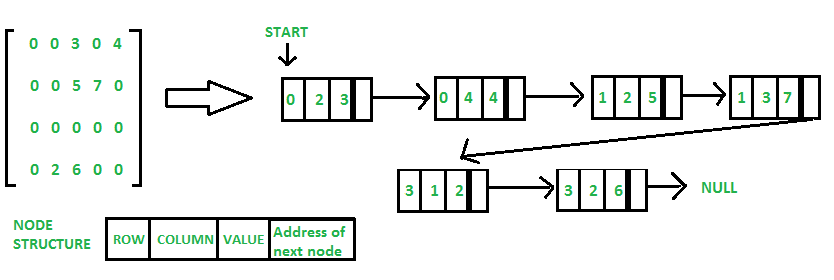
0 0 3 0 4            
0 0 5 7 0
0 0 0 0 0
0 2 6 0 0

Representing a sparse matrix by a 2D array leads to wastage of lots of memory as zeroes in the matrix are of no use in most of the cases. So, instead of storing zeroes with non-zero elements, we only store non-zero elements. This means storing non-zero elements with triples- (Row, Column, value). 

Sparse Matrix Representations can be done in many ways following are two common representations: 

1. Array representation
2. Linked list representation

Method 1: Using Arrays:
2D array is used to represent a sparse matrix in which there are three rows named as 

• Row: Index of row, where non-zero element is located
• Column: Index of column, where non-zero element is located
• Value: Value of the non zero element located at index – (row,column)

// C++ program for Sparse Matrix Representation

// using Array

#include<stdio.h>

 

int main()

{

    // Assume 4x5 sparse matrix

    int sparseMatrix[4][5] =

    {

        {0 , 0 , 3 , 0 , 4 },

        {0 , 0 , 5 , 7 , 0 },

        {0 , 0 , 0 , 0 , 0 },

        {0 , 2 , 6 , 0 , 0 }

    };

 

    int size = 0;

    for (int i = 0; i < 4; i++)

        for (int j = 0; j < 5; j++)

            if (sparseMatrix[i][j] != 0)

                size++;

 

    // number of columns in compactMatrix (size) must be

    // equal to number of non - zero elements in

    // sparseMatrix

    int compactMatrix[3][size];

 

    // Making of new matrix

    int k = 0;

    for (int i = 0; i < 4; i++)

        for (int j = 0; j < 5; j++)

            if (sparseMatrix[i][j] != 0)

            {

                compactMatrix[0][k] = i;

                compactMatrix[1][k] = j;

                compactMatrix[2][k] = sparseMatrix[i][j];

                k++;

            }

 

    for (int i=0; i<3; i++)

    {

        for (int j=0; j<size; j++)

            printf("%d ", compactMatrix[i][j]);

 

        printf("\n");

    }

    return 0;

}




Output: 

0 0 1 1 3 3 
2 4 2 3 1 2 
3 4 5 7 2 6

Method 2: Using Linked Lists
In linked list, each node has four fields. These four fields are defined as: 

• Row: Index of row, where non-zero element is located
• Column: Index of column, where non-zero element is located
• Value: Value of the non zero element located at index – (row,column)
• Next node: Address of the next node

 // C program for Sparse Matrix Representation

// using Linked Lists

#include<stdio.h>

#include<stdlib.h>

 

// Node to represent sparse matrix

struct Node

{

    int value;

    int row_position;

    int column_postion;

    struct Node *next;

};

 

// Function to create new node

void create_new_node(struct Node** start, int non_zero_element,

                     int row_index, int column_index )

{

    struct Node *temp, *r;

    temp = *start;

    if (temp == NULL)

    {

        // Create new node dynamically

        temp = (struct Node *) malloc (sizeof(struct Node));

        temp->value = non_zero_element;

        temp->row_position = row_index;

        temp->column_postion = column_index;

        temp->next = NULL;

        *start = temp;

 

    }

    else

    {

        while (temp->next != NULL)

            temp = temp->next;

 

        // Create new node dynamically

        r = (struct Node *) malloc (sizeof(struct Node));

        r->value = non_zero_element;

        r->row_position = row_index;

        r->column_postion = column_index;

        r->next = NULL;

        temp->next = r;

 

    }

}

 

// This function prints contents of linked list

// starting from start

void PrintList(struct Node* start)

{

    struct Node *temp, *r, *s;

    temp = r = s = start;

 

    printf("row_position: ");

    while(temp != NULL)

    {

 

        printf("%d ", temp->row_position);

        temp = temp->next;

    }

    printf("\n");

 

    printf("column_postion: ");

    while(r != NULL)

    {

        printf("%d ", r->column_postion);

        r = r->next;

    }

    printf("\n");

    printf("Value: ");

    while(s != NULL)

    {

        printf("%d ", s->value);

        s = s->next;

    }

    printf("\n");

}

 

 

// Driver of the program

int main()

{

   // Assume 4x5 sparse matrix

    int sparseMatric[4][5] =

    {

        {0 , 0 , 3 , 0 , 4 },

        {0 , 0 , 5 , 7 , 0 },

        {0 , 0 , 0 , 0 , 0 },

        {0 , 2 , 6 , 0 , 0 }

    };

 

    /* Start with the empty list */

    struct Node* start = NULL;

 

    for (int i = 0; i < 4; i++)

        for (int j = 0; j < 5; j++)

 

            // Pass only those values which are non - zero

            if (sparseMatric[i][j] != 0)

                create_new_node(&start, sparseMatric[i][j], i, j);

 

    PrintList(start);

 

    return 0;

}

Output: 

row_position: 0 0 1 1 3 3 
column_postion: 2 4 2 3 1 2 
Value: 3 4 5 7 2 6              

Other representations: 
As a Dictionary where row and column numbers are used as keys and values are matrix entries. This method saves space but sequential access of items is costly.

As a list of list. The idea is to make a list of rows and every item of list contains values. We can keep list items sorted by column numbers.