Derivation of Index Formulae for 3-D and n-D Array

Calculate the address of any element in the 3-D Array: 

A 3-Dimensional array is a collection of 2-Dimensional arrays. It is specified by using three subscripts:

1. Block size
2. Row size
3. Column size

More dimensions in an array mean more data can be stored in that array. 

Example:

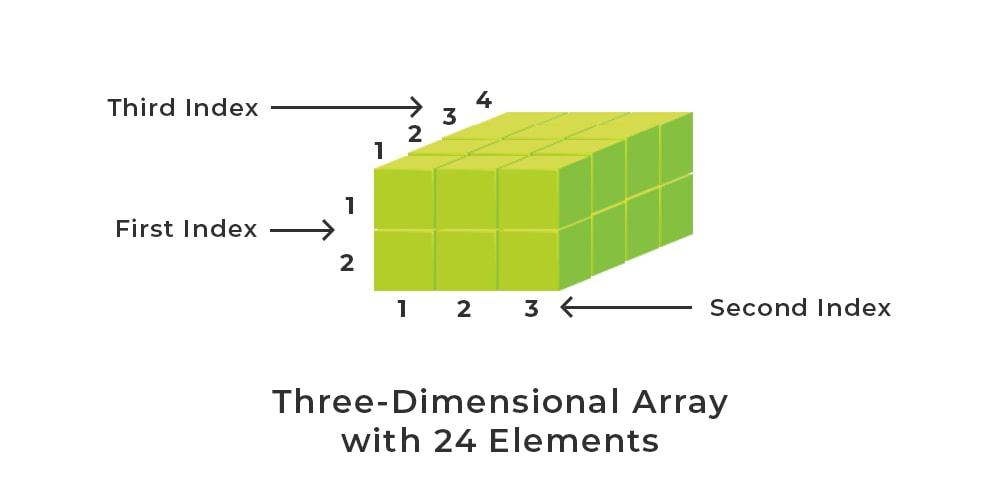
3-D array

To find the address of any element in 3-Dimensional arrays there are the following two ways-

• Row Major Order
• Column Major Order

1. Row Major Order:

To find the address of the element using row-major order, use the following formula:

Address of A[i][j][k] = B + W (M * N(i-x) + N *(j-y) + (k-z))

Here:

B = Base Address (start address)

W = Weight (storage size of one element stored in the array)

M = Row (total number of rows)

N = Column (total number of columns)

P = Width (total number of cells depth-wise)

x = Lower Bound of Row

y = Lower Bound of Column

z = Lower Bound of Width

Example: Given an array, arr[1:9, -4:1, 5:10] with a base value of 400 and the size of each element is 2 Bytes in memory find the address of element arr[5][-1][8] with the help of row-major order?

Solution:

Given:

Row Subset of an element whose address to be found I = 5

Column Subset of an element whose address to be found J = -1 

Block Subset of an element whose address to be found K = 8

Base address B = 400

Storage size of one element store in any array(in Byte) W = 2

Lower Limit of row/start row index of matrix x = 1

Lower Limit of column/start column index of matrix y = -4 

Lower Limit of blocks in matrix z = 5

M = Upper Bound – Lower Bound + 1 = 1 – (-4) + 1 = 6

N = Upper Bound – Lower Bound + 1 = 10 – 5 + 1 = 6 

Formula used:                                                

Address of[I][J][K] =B + W (M * N(i-x) + N *(j-y) + (k-z))

Solution:

Address of[][][] = 400 + 2 * {[6 * 6 * (5 – 1)] + 6 * [(-1 + 4)]} + [8 – 5]

                             = 400 + 2 * ((4 * 6 + 3) * 6 + 3)

                            = 400 + 2 * (165)

                           = 730

2. Column Major Order:

To find the address of the element using column-major order, use the following formula:1

Address of A[i][j][k = B + W(M * N(i – x) + M *(k – z) + (j – y))

Here:

B = Base Address (start address)

W = Weight (storage size of one element stored in the array)

M = Row (total number of rows)

N = Column (total number of columns)

P = Width (total number of cells depth-wise)

x = Lower Bound of Row

y = Lower Bound of Column

z = Lower Bound of Width

Example: Given an array arr[1:8, -5:5, -10:5] with a base value of 400 and the size of each element is 4 Bytes in memory find the address of element arr[3][3][3] with the help of column-major order?

Solution:

Given:

Row Subset of an element whose address to be found I = 3

Column Subset of an element whose address to be found J = 3

Block Subset of an element whose address to be found K = 3

Base address B = 400

Storage size of one element store in any array(in Byte) W = 4

Lower Limit of row/start row index of matrix x = 1

Lower Limit of column/start column index of matrix y = -5

Lower Limit of blocks in matrix z = -10

M = Upper Bound – Lower Bound + 1 = 5 + 5 + 1 = 11

N = Upper Bound – Lower Bound + 1 = 5 + 10 + 1 = 16 

Formula used:

Address of[i][j][k] = B + W(M * N(i – x) + M * (k – z) + (j – y))

Solution:

Address of[3][3][3] = 400 + 4 * {[(3 – 1)] * 16 + [3 + 10] ]} * 11 + [3 + 5]

                                    = 400 + 4 * ((32 + 13) * 11 + 8)

                                   = 400 + 4 * (503)

                                  = 400 + 2012

                                 = 2412

N-Dimensional Arrays: 

The N-Dimensional array is basically an array of arrays. As 1-D arrays are identified as a single index, 2-D arrays are identified using two indices, similarly, N-Dimensional arrays are identified using N indices. A multi-dimensional array is declared as follows:

int NDA[S1][S2][S3]……..[SN];

Explanation:

• Here, NDA is the name of the N-Dimensional array. It can be any valid identifier name.
• In the above syntax, S1, S2, S3……SN denotes the max sizes of the N dimensions.
• The lower bounds are assumed to be zeroes for all the dimensions.
• The above array is declared as an integer array. It can be any valid data type other than an integer as well.

Address Calculation of N-Dimensional Arrays:

Assumptions:

• The N-Dimensional array NDA with the maximum sizes of N dimensions are S1, S2, S3, ………, SN.
• The element whose address needs to be calculated has indices l1, l2, l3, …………..lN respectively.
• It is possible that the array indices do not have the lower bound as zero. For example, consider the following array T: T[-5…5][2……9][14…54][-9…-2].

Explanation:

• In the above array T, the lower bounds of indices are not zeroes.
• So that the sizes of the indices of the array are different now and can be calculated by using the formula:

UpperBound – LowerBound +1

• So, here the S1 = 5 – (-5) + 1 = 11. Similarly, S2 = 8, S3 = 41 and S4 = 8.

For address calculation, the lower bounds are t1, t2, t3…….tN. There exist two ways to store the array elements:

• Row Major
• Column Major

The Column Major formula:

Address of NDA[I1][I2]. . . [IN] = BAd + W*[((…ENSN-1+ EN-1 )SN-2 +… E3 )S2+ E2 )S1 +E1]

• BAd represents the base address of the array.
• W is Storage Size of one element stored in the array (in byte).
• Also, Ei is given by Ei  = li – ti, where li and ti are the calculated indexes (indices of array element which needs to be determined) and lower bounds respectively.

The Row Major formula:

Address of NDA[I1][I2]. . . .[lN] = BAd + W*[((E1S2 + E2 )S3 +E3 )S4 ….. + EN-1 )SN + EN]

The simplest way to learn the formulas:

For row-major: If width = 5, the interior sequence is E1S2 + E2S3 + E3S4 + E4S5 + E5 and if width = 3, the interior sequence is E1S2 + E2S3 + E3. Figure out the pattern in the order and follow four basic steps for the formula of any width:

• Write the interior sequence.
• Put the closing bracket after each E except the first term. So for width = 5, it becomes

E1S2 + E2)S3 + E3)S4 + E4)S5 + E5).

 

• Put all the Opening brackets initially.

((((E1S2 + E2)S3 + E3)S4 + E4)S5 + E5).

 

• Incorporate the base address and width in the formula.

The approach is similar for the Column Major but the pattern of the interior sequence is reverse of the row-major pattern. 

For column-major: If width =5, the interior sequence is E5S4 + E4S3 + E3S2+ E2S1 + E1.

Example: Let’s take a multi-dimensional array A[10][20][30][40] with the base address 1200. The task is to find the address of element A[1][3][5][6].

Here, BAd = 1200 and width = 4.

S1 = 10, S2 = 20, S3 = 30, S4 = 40

Since the lower bounds are not given, so lower bounds are assumed to be zero.

E1 = 1 – 0 = 1; 

E2 = 3 – 0 = 3; 

E3 = 5 – 0 = 5;

E4 = 6 – 0 = 6.

Any of the techniques (Row-major or column-major) can be used for calculating the answer (unless specified). 

By applying the formula for row-major, directly write the formula as:

A[1][3][5][6] = 1200 + 4(((1 × 20 + 3)30 +5)40 + 6) 

 =1200 +4((23 × 30 +5)40 +6) 

=1200 + 4(695 × 40 + 6) 

=1200 + (4 × 27806) 

=112424.

Example: Suppose multidimensional array A and B are declared using A [-2:2, 2:22] and B [1:8, -5:5, -10:5].

1.      Find out the length of each dimension and number of elements in array A and B.

2.     Consider B [3, 3, 3] elements in array B find effective address E1, E2 and E3. Also find out the real address of these elements. (In this case the base address of array B is 400 and W is 4)

AKTU 2018-19, Marks 07

Answer:       For array A

   L1 = UB –LB +1                                L2  = UB –LB +1

        =2 – (-2) +1                                     =22 – 2 + 1

        = 4 + 1 = 5                                       = 21

For array B

L1 = UB –LB +1                 L2= UB –LB +1                    L3= UB –LB +1

      = 8 – 1 + 1                     = 5 – (-5) +1                      =5 – (-10) +1

      = 8                                 = 11                                   = 16

Total number of elements in array B is: L1 X L2 X L3 = 8 X 11 X 16 = 1408.

Here in given question Ki = 3, 3, 3 therefore K1=3, k2 = 3 and K3 = 3

        LB1= 1, LB2 = -5 LB3 = -10

        E1 = K1 – LB1 = 3 – 1 = 2

        E2 = K2 – LB2 = 3- (-5) = 8

        E3 = K3 – LB3 = 3 – (-10) = 13

The real address Row – by- Row:

= Base (A) + W [ (E1L2 + E2) L3 + E3]

        = 400 + 4 [(2 (11) + 8) 16 + 13]

        = 400 + 4 [(22+8) 16 + 13]

        = 400 + 4 [(30) 16 + 13]

        = 400 + 4 [480 + 13]

        = 400 + 4 [493]

        = 400 + 1972

        = 2372

The real address Column – by – column:

        = Base (A) + W [(E3L2 +E2) L1 + E1]

        = 400 + 4 [(13(11) + 8) 8 + 2]

        = 400 +4 [(143 + 8) 8 + 2]

        = 400 + 4[(151) 8 + 2)]

        = 400 + 4[1208 + 2]

        = 400 + 4840

        = 5240

Ques. Given an array [ 1..8, 1..5, 1..7 ] of integers. Calculate address of element A[5,3,6], by using rows and columns methods, if BA=900?
Solution:- The dimensions of A are :
          M=8 , N=5, R=7, i=5, j=3, k=6
          Rows - wise : 
          Location (A[i,j,k]) = BA + MN(k-1) + N(i-1) + (j-1)
          Location(A[5,3,6])= 900 + 8x5(6-1) + 5(5-1) + (3-1)
                      = 900 + 40 x 5 +5 x 4 + 2
                      = 900 + 200 +20 +2
                      = 1122
          Columns - wise : 
          Location (A[i,j,k]) = BA + MN(k-1) + M(j-1) + (i-1)
          Location (A[5,3,6]) = 900 + 8x5(6-1) + 8(3-1) + (5-1)
                      = 900 + 40 x 5 +8 x 2 + 4
                      = 900 + 200 +16 +4
                      = 1120