A graph which has no cycle is called an acyclic graph. A tree is an acyclic graph or graph having no cycles.
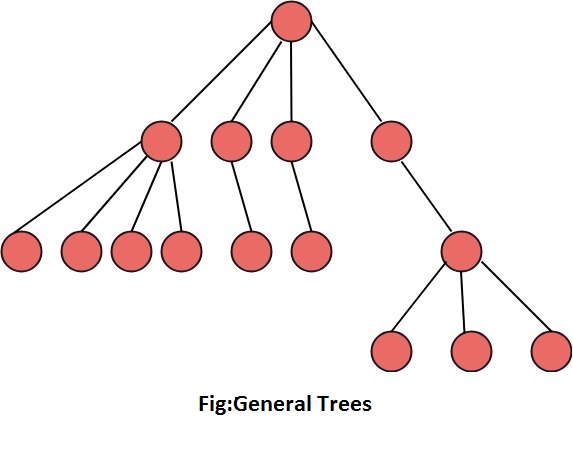
A tree or general trees is defined as a non-empty finite set of elements called vertices or nodes having the property that each node can have minimum degree 1 and maximum degree n. It can be partitioned into n+1 disjoint subsets such that the first subset contains the root of the tree and remaining n subsets includes the elements of the n subtree.
Directed Trees:
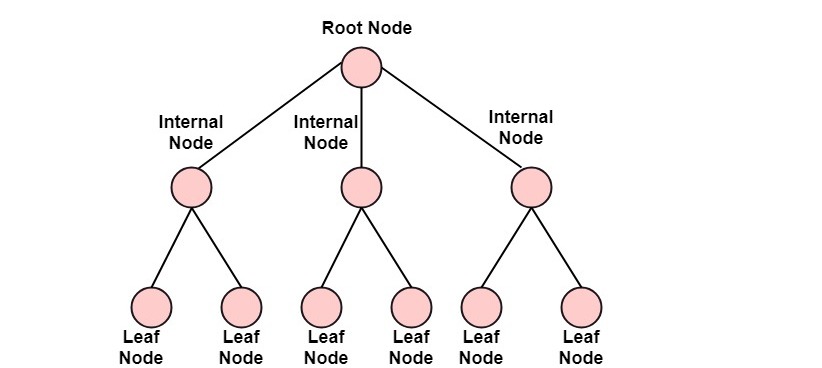
A directed tree is an acyclic directed graph. It has one node with indegree 1, while all other nodes have indegree 1 as shown in fig:
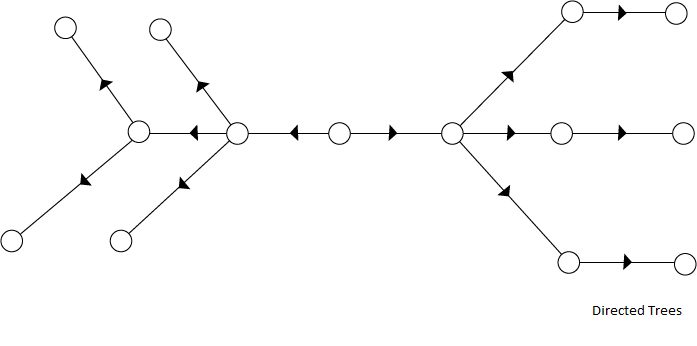
The node which has outdegree 0 is called an external node or a terminal node or a leaf. The nodes which have outdegree greater than or equal to one are called internal node.
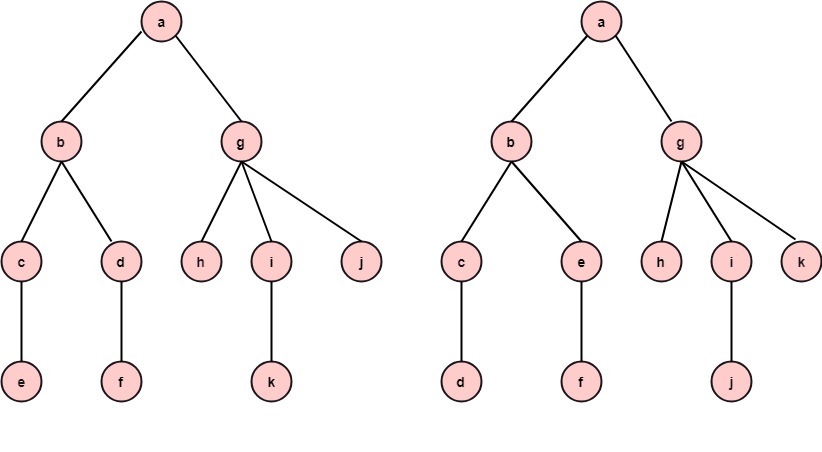
Ordered Trees:
If in a tree at each level, an ordering is defined, then such a tree is called an ordered tree.
Example: The trees shown in the figures represent the same tree but have different orders.
Properties of Trees:
- There is only one path between each pair of vertices of a tree.
- If a graph G there is one and only one path between each pair of vertices G is a tree.
- A tree T with n vertices has n-1 edges.
- A graph is a tree if and only if it a minimal connected.
Rooted Trees:
If a directed tree has exactly one node or vertex called root whose incoming degrees is 0 and all other vertices have incoming degree one, then the tree is called rooted tree.
Note: 1. A tree with no nodes is a rooted tree (the empty tree)
2. A single node with no children is a rooted tree.
Path length of a Vertex:
The path length of a vertex in a rooted tree is defined to be the number of edges in the path from the root to the vertex.
Example: Find the path lengths of the nodes b, f, l, q as shown in fig:
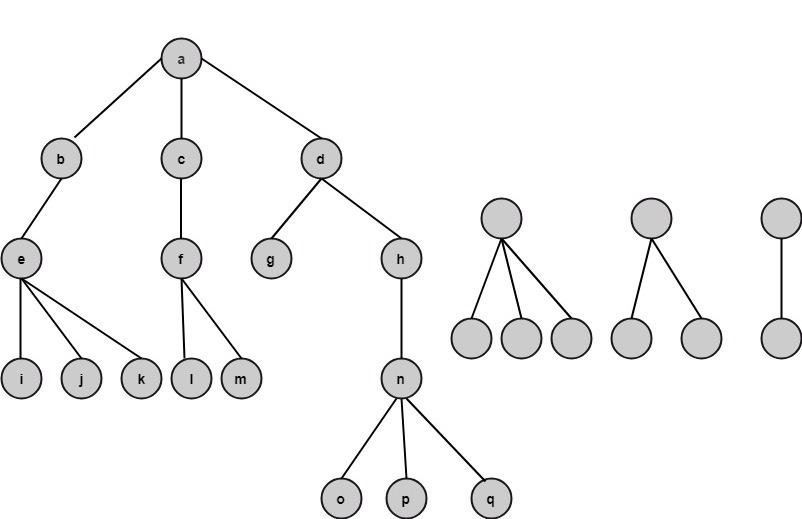
Solution: The path length of node b is one.
The path length of node f is two.
The path length of node l is three
The path length of the node q is four.




No comments:
Post a Comment