Concept Learning

What is Concept Learning…?

“A task of acquiring potential hypothesis (solution) that best fits the given training examples.”

Concept Learning Task

Consider the example task of learning the target concept “days on which my friend Prabhas enjoys his favorite water sport.”

Below Table describes a set of example days, each represented by a set of attributes. The attribute EnjoySport indicates whether or not Prabhas enjoys his favorite water sport on this day. The task is to learn to predict the value of EnjoySport for an arbitrary day, based on the values of its other attributes.

Concept Learning Task Example

Concept Learning Task Notation

Concept Learning Task Notation 2

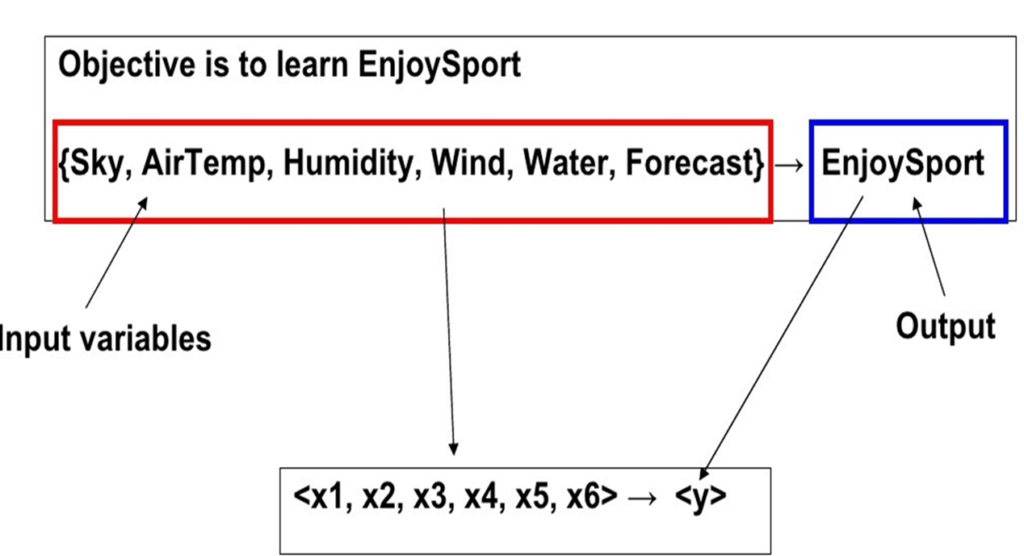
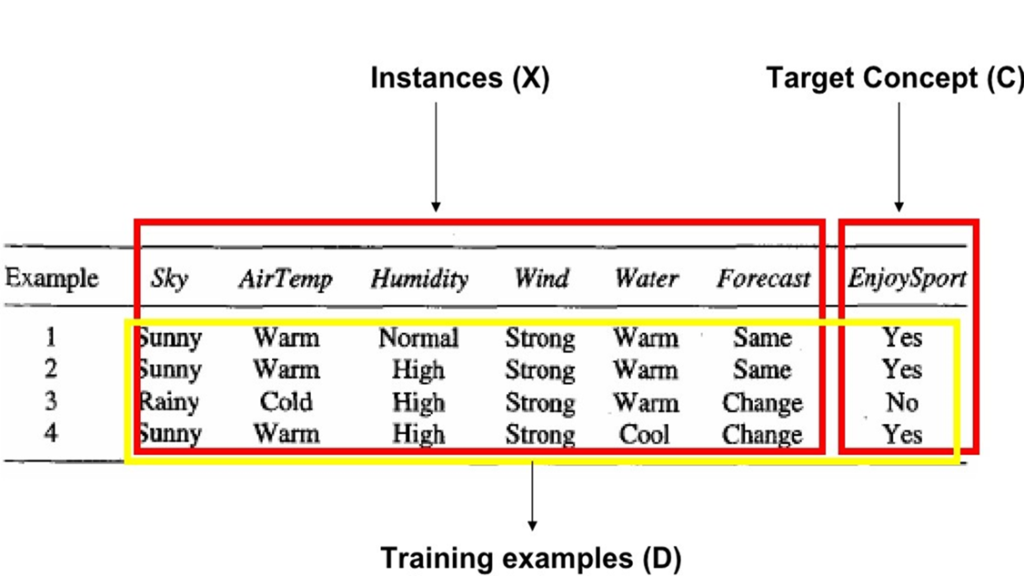
What hypothesis representation shall we provide to the learner in this case?

Let us begin by considering a simple representation in which each hypothesis consists of a conjunction of constraints on the instance attributes.

In particular, let each hypothesis be a vector of six constraints, specifying the values of the six attributes Sky, AirTemp, Humidity, Wind, Water, and Forecast.

For each attribute, the hypothesis will either

• indicate by a “?’ that any value is acceptable for this attribute,

• specify a single required value (e.g., Warm) for the attribute, or

• indicate by a “ø” that no value is acceptable.

If some instance x satisfies all the constraints of hypothesis h, then h classifies x as a positive example (h(x) = 1).

To illustrate, the hypothesis that Prabhas enjoys his favorite sport only on cold days with high humidity (independent of the values of the other attributes) is represented by the expression

(?, Cold, High, ?, ?, ?)

Most General and Specific Hypothesis

The most general hypothesis-that every day is a positive example-is represented by

(?, ?, ?, ?, ?, ?)

and the most specific possible hypothesis-that no day is a positive example-is represented by

(ø, ø, ø, ø, ø, ø)

A CONCEPT LEARNING TASK – Search

Concept learning can be viewed as the task of searching through a large space of hypotheses implicitly defined by the hypothesis representation.

The goal of this search is to find the hypothesis that best fits the training examples.

It is important to note that by selecting a hypothesis representation, the designer of the learning algorithm implicitly defines the space of all hypotheses that the program can ever represent and therefore can ever learn.

Instance Space

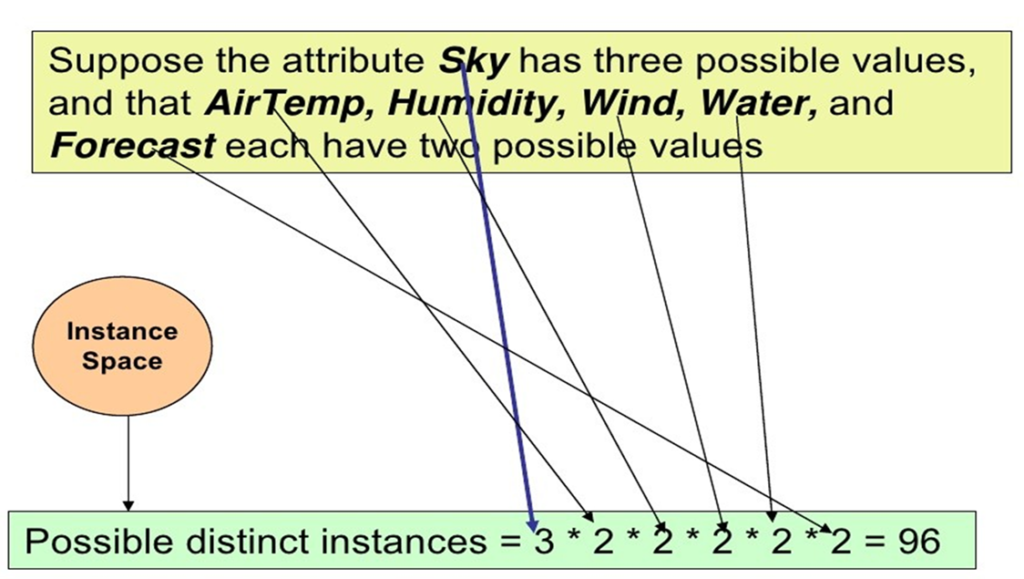
Consider, for example, the instances X and hypotheses H in the EnjoySport learning task.

Given that the attribute Sky has three possible values, and that AirTemp, Humidity, Wind, Water, and Forecast each have two possible values, the instance space X contains exactly 3 . 2 . 2 . 2 . 2 . 2 = 96 distinct instances.

Example:

Let’s assume there are two features F1 and F2 with F1 has A and B as possibilities and F2 as X and Y as possibilities.

F1  – > A, B

F2  – > X, Y

Instance Space: (A, X), (A, Y), (B, X), (B, Y) – 4 Examples

Hypothesis Space: (A, X), (A, Y), (A, ø), (A, ?), (B, X), (B, Y), (B, ø), (B, ?), (ø, X), (ø, Y), (ø, ø), (ø, ?), (?, X), (?, Y), (?, ø), (?, ?)  – 16

Hypothesis Space: (A, X), (A, Y), (A, ?), (B, X), (B, Y), (B, ?), (?, X), (?, Y (?, ?) – 10

Instance Space

Hypothesis Space

Similarly there are 5 . 4 . 4 . 4 . 4 . 4 = 5120 syntactically distinct hypotheses within H.

Notice, however, that every hypothesis containing one or more “ø” symbols represents the empty set of instances; that is, it classifies every instance as negative.

Therefore, the number of semantically distinct hypotheses is only 1 + (4 . 3 . 3 . 3 . 3 . 3) = 973.

Our EnjoySport example is a very simple learning task, with a relatively small, finite hypothesis space.

General-to-Specific Ordering of Hypotheses

To illustrate the general-to-specific ordering, consider the two hypotheses

h1 = (Sunny, ?, ?, Strong, ?, ?)

h2 = (Sunny, ?, ?, ?, ?, ?)

Now consider the sets of instances that are classified positive by hl and by h2. Because h2 imposes fewer constraints on the instance, it classifies more instances as positive.

In fact, any instance classified positive by h1 will also be classified positive by h2. Therefore, we say that h2 is more general than h1.

For any instance x in X and hypothesis h in H, we say that x satisjies h if and only if h(x) = 1.

We define the more_general_than_or_equale_to relation in terms of the sets of instances that satisfy the two hypotheses.

More General Than Hypothesis

Concept learning is a fundamental problem in machine learning, where the goal is to infer a general rule or concept from specific examples. In concept learning, the machine tries to identify a hypothesis (or rule) that best explains the relationship between input features and their corresponding output labels based on the training data. This can be thought of as finding a function that can classify new examples correctly based on what was learned from the training set.

Key Terminology in Concept Learning:

1. Concept: A rule or a classification that we want to learn.
2. Hypothesis: A proposed solution or rule that describes the concept based on the training examples.
3. Target Concept: The true concept that we are trying to learn.
4. Instance: A single data point described by a set of features or attributes.
5. Positive Examples: Instances that belong to the target concept (labeled as "true").
6. Negative Examples: Instances that do not belong to the target concept (labeled as "false").
7. Hypothesis Space: The set of all possible hypotheses that could describe the concept.

Concept Learning Problem

In concept learning, we want to find a hypothesis $h$ from a hypothesis space $H$ that is consistent with the given set of training examples $D$, where each example is labeled as either a positive or negative instance of the concept. The task is to find the hypothesis that best matches the target concept $c$, which can classify unseen examples correctly.

General-to-Specific Ordering

In concept learning, hypotheses are often organized in a general-to-specific ordering:

• A general hypothesis covers a broad range of instances and may classify some irrelevant instances as positive examples.
• A specific hypothesis applies to fewer instances and may miss some relevant positive examples.

The goal is to find a hypothesis that is neither too general (overfitting) nor too specific (underfitting) and that can classify unseen instances accurately.

Example of Concept Learning

Let’s consider a simple example where we want to learn the concept of a "safe car" based on some features. Assume the following features describe each car:

• Color (Red, Blue, Green, etc.)
• Type (SUV, Sedan, Convertible, etc.)
• Origin (Domestic or Imported)
• Age (New or Old)

Now, we are given the following training examples (with labels indicating whether each car is "safe" or not):

Color	Type	Origin	Age	Safe Car?
Red	SUV	Domestic	New	Yes
Blue	Sedan	Imported	Old	No
Red	Sedan	Imported	New	Yes
Green	SUV	Domestic	Old	No
Red	SUV	Imported	New	Yes

Our goal is to learn the concept of a "safe car" from these examples.

Step 1: Hypothesis Representation

The hypothesis will be represented as a conjunction of attribute values. For instance:

• $h_1$: (Color = Red) AND (Type = SUV) AND (Origin = Domestic) AND (Age = New)

This is a specific hypothesis because it only classifies a car as safe if it exactly matches all of these feature values.

Step 2: General-to-Specific Search

We start with the most specific hypothesis that matches the first positive example. This is the most specific description of a "safe car" based on the first positive instance:

• After the first positive example (Red, SUV, Domestic, New), the hypothesis is:
  • $h_1$: (Color = Red) AND (Type = SUV) AND (Origin = Domestic) AND (Age = New)

This hypothesis matches the first example perfectly, but it is very restrictive.

Step 3: Updating the Hypothesis

As we encounter more examples, we generalize the hypothesis to fit additional positive examples and exclude negative examples.

• After seeing the second positive example (Red, Sedan, Imported, New), we update the hypothesis to:
  • $h_2$: (Color = Red) AND (Age = New)

We generalized the hypothesis by dropping the attributes Type and Origin because these values do not need to be the same across all positive examples.

Step 4: Final Hypothesis

After processing all examples, the most general hypothesis that still covers all the positive examples is:

• $h$: (Color = Red) AND (Age = New)

This hypothesis classifies a car as safe if it is red and new, regardless of its type or origin.

Step 5: Classifying New Instances

Now, we can use this learned hypothesis to classify new instances:

• Example 1: (Red, SUV, Domestic, New) → Safe (because it satisfies the hypothesis).
• Example 2: (Blue, SUV, Domestic, New) → Not Safe (because it does not satisfy the hypothesis).
• Example 3: (Red, Sedan, Imported, Old) → Not Safe (because it does not satisfy the "New" condition).

Hypothesis Space and Search Strategy

The hypothesis space $H$ contains all possible hypotheses that can be formed by combining the features. In concept learning, we typically use a general-to-specific search strategy to explore the hypothesis space. We start with the most specific hypothesis and gradually generalize it based on the training examples until we find a consistent hypothesis that fits the data.

Conclusion

In concept learning, the goal is to find a hypothesis that best describes the relationship between input features and output labels. The Naive Bayes Classifier learns the most likely concept given the training data, while other concept-learning approaches, like the Find-S Algorithm, employ a general-to-specific search strategy. The key challenge is balancing generalization and specificity to create a hypothesis that can classify new, unseen instances correctly.