EM Algorithm

What is EM Algorithm ?

EM algorithm was proposed in 1997 by Arthur Dempster, Nan Laird, and Donald Rubin. It is basically used to find the local maximum likelihood parameters of a statistical model in case the latent variables are present or the data is missing or incomplete.

The EM Algorithm follows the following steps in order to find the relevant model parameters in the presence of latent variables.

1. Consider a set of starting parameters in incomplete data.

2. Expectation Step – This step is used to estimate the values of the missing values in the data. It involves the observed data to basically guess the values in the missing data.

3. Maximization Step – This step generates complete data after the Expectation step updates the missing values in the data.

4. Execute the step 2 and 3 until the convergence is met.

Convergence – The concept of convergence in probability is based on intuition. Let’s say we have two random variables if the probability of their difference is very small, it is said to be converged. In this case, convergence means if the values match each other.

How Does It Work?

The basic idea behind the EM algorithm is to use the observed data to estimate the missing data and then updating those values of the parameters. keeping the flowchart in mind, let us understand how the EM algorithm works.

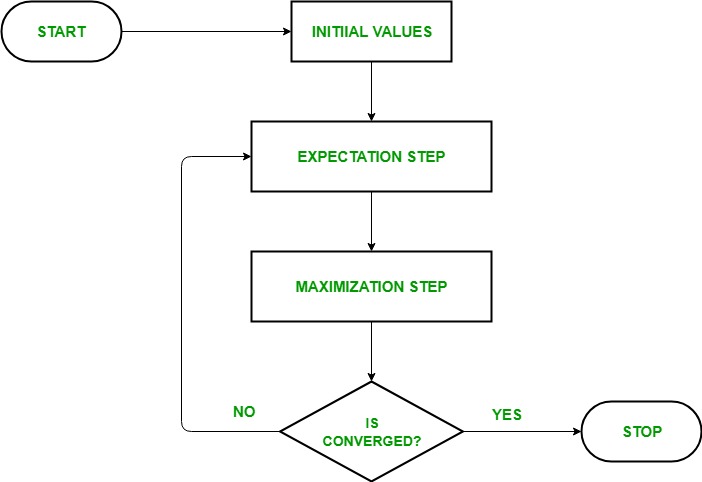
1. In the starting stage, a set of initial parameters is considered. A set of unobserved and incomplete data is given to the system with an assumption that the observed data is coming from a specific model.
2. The next step is the Expectation Step or E-STEP. In this step, we use the observed data to estimate missing or incomplete data. It is basically used to update the variables.
3. The Maximization step or M-STEP is used to complete the data generated in the E-STEP. This step basically updates the hypothesis.
4. In the last step, it is checked whether the values are converging or not. If the values match, then we do nothing, else we will continue with step 2 and 3 until the convergence is met.

The EM algorithm is also known for clustering other than density estimation. So, let us try to understand the EM algorithm with the help of the Gaussian Mixture Model.

Gaussian Mixture Model

The GMM or Gaussian Mixture Model is a mixture model that uses a combination of probability distributions and also requires the estimation of mean and standard deviation parameters.

Even though there are a lot of techniques to estimate the parameters for a Gaussian Mixture Model, the most common technique is the Maximum Likelihood estimation.

Let us consider a case, where the data points are generated by two different processes and each process has a Gaussian probability distribution. But it is unclear, which distribution a given data point belongs to since the data is combined and distributions are similar. And the processes used for generating the data points represent the latent variables and influence the data. The EM algorithm seems like the best approach to estimate the parameters of the distributions.

In the EM algorithm, the E-STEP would estimate the expected value for each latent variable and the M-STEP would optimize the parameters of the distribution using the Maximum Likelihood.

Usage of EM algorithm –

• It can be used to fill the missing data in a sample.
• It can be used as the basis of unsupervised learning of clusters.
• It can be used for the purpose of estimating the parameters of Hidden Markov Model (HMM).
• It can be used for discovering the values of latent variables.

Advantages of EM algorithm –

• It is always guaranteed that likelihood will increase with each iteration.
• The E-step and M-step are often pretty easy for many problems in terms of implementation.
• Solutions to the M-steps often exist in the closed form.

Disadvantages of EM algorithm –

• It has slow convergence.
• It makes convergence to the local optima only.
• It requires both the probabilities, forward and backward (numerical optimization requires only forward probability).