Naïve Bayes Classifier Algorithm
- Naïve Bayes algorithm is a supervised learning algorithm, which is based on Bayes theorem and used for solving classification problems.
- It is mainly used in text classification that includes a high-dimensional training dataset.
- Naïve Bayes Classifier is one of the simple and most effective Classification algorithms which helps in building the fast machine learning models that can make quick predictions.
- It is a probabilistic classifier, which means it predicts on the basis of the probability of an object.
- Some popular examples of Naïve Bayes Algorithm are spam filtration, Sentimental analysis, and classifying articles.
Why is it called Naïve Bayes?
The Naïve Bayes algorithm is comprised of two words Naïve and Bayes, Which can be described as:
- Naïve: It is called Naïve because it assumes that the occurrence of a certain feature is independent of the occurrence of other features. Such as if the fruit is identified on the bases of color, shape, and taste, then red, spherical, and sweet fruit is recognized as an apple. Hence each feature individually contributes to identify that it is an apple without depending on each other.
- Bayes: It is called Bayes because it depends on the principle of Bayes' Theorem.
Bayes' Theorem:
- Bayes' theorem is also known as Bayes' Rule or Bayes' law, which is used to determine the probability of a hypothesis with prior knowledge. It depends on the conditional probability.
- The formula for Bayes' theorem is given as:
Where,
P(A|B) is Posterior probability: Probability of hypothesis A on the observed event B.
P(B|A) is Likelihood probability: Probability of the evidence given that the probability of a hypothesis is true.
P(A) is Prior Probability: Probability of hypothesis before observing the evidence.
P(B) is Marginal Probability: Probability of Evidence.
Working of Naïve Bayes' Classifier:
Working of Naïve Bayes' Classifier can be understood with the help of the below example:
Suppose we have a dataset of weather conditions and corresponding target variable "Play". So using this dataset we need to decide that whether we should play or not on a particular day according to the weather conditions. So to solve this problem, we need to follow the below steps:
- Convert the given dataset into frequency tables.
- Generate Likelihood table by finding the probabilities of given features.
- Now, use Bayes theorem to calculate the posterior probability.
Problem: If the weather is sunny, then the Player should play or not?
Solution: To solve this, first consider the below dataset:
| Outlook | Play | |
|---|---|---|
| 0 | Rainy | Yes |
| 1 | Sunny | Yes |
| 2 | Overcast | Yes |
| 3 | Overcast | Yes |
| 4 | Sunny | No |
| 5 | Rainy | Yes |
| 6 | Sunny | Yes |
| 7 | Overcast | Yes |
| 8 | Rainy | No |
| 9 | Sunny | No |
| 10 | Sunny | Yes |
| 11 | Rainy | No |
| 12 | Overcast | Yes |
| 13 | Overcast | Yes |
Frequency table for the Weather Conditions:
| Weather | Yes | No |
| Overcast | 5 | 0 |
| Rainy | 2 | 2 |
| Sunny | 3 | 2 |
| Total | 10 | 5 |
Likelihood table weather condition:
| Weather | No | Yes | |
| Overcast | 0 | 5 | 5/14= 0.35 |
| Rainy | 2 | 2 | 4/14=0.29 |
| Sunny | 2 | 3 | 5/14=0.35 |
| All | 4/14=0.29 | 10/14=0.71 |
Applying Bayes'theorem:
P(Yes|Sunny)= P(Sunny|Yes)*P(Yes)/P(Sunny)
P(Sunny|Yes)= 3/10= 0.3
P(Sunny)= 0.35
P(Yes)=0.71
So P(Yes|Sunny) = 0.3*0.71/0.35= 0.60
P(No|Sunny)= P(Sunny|No)*P(No)/P(Sunny)
P(Sunny|NO)= 2/4=0.5
P(No)= 0.29
P(Sunny)= 0.35
So P(No|Sunny)= 0.5*0.29/0.35 = 0.41
So as we can see from the above calculation that P(Yes|Sunny)>P(No|Sunny)
Hence on a Sunny day, Player can play the game.
Example-2
Let’s consider a simple binary classification problem where we want to classify whether an email is spam or not spam based on three features:
- Whether the email contains the word "offer."
- Whether the email contains the word "free."
- Whether the email contains the word "win."
We have the following training data:
| Contains "offer" | Contains "free" | Contains "win" | Class (Spam/Not Spam) | |
|---|---|---|---|---|
| Email 1 | Yes | No | Yes | Spam |
| Email 2 | No | Yes | No | Not Spam |
| Email 3 | Yes | Yes | No | Spam |
| Email 4 | No | No | Yes | Not Spam |
We want to classify a new email that contains "offer" and "win" but does not contain "free."
Step 1: Calculate Prior Probabilities
We first calculate the prior probabilities of each class (spam or not spam) based on the training data.
- P(Spam) = Number of Spam Emails / Total Number of Emails = 2 / 4 = 0.5
- P(Not Spam) = Number of Not Spam Emails / Total Number of Emails = 2 / 4 = 0.5
Step 2: Calculate Likelihoods for Each Feature
Next, we calculate the likelihoods of each feature given the class.
For the class Spam:
- P(Contains "offer" | Spam) = Number of Spam Emails containing "offer" / Total Spam Emails = 1 / 2 = 0.5
- P(Contains "free" | Spam) = Number of Spam Emails containing "free" / Total Spam Emails = 1 / 2 = 0.5
- P(Contains "win" | Spam) = Number of Spam Emails containing "win" / Total Spam Emails = 1 / 2 = 0.5
For the class Not Spam:
- P(Contains "offer" | Not Spam) = Number of Not Spam Emails containing "offer" / Total Not Spam Emails = 0 / 2 = 0
- P(Contains "free" | Not Spam) = Number of Not Spam Emails containing "free" / Total Not Spam Emails = 1 / 2 = 0.5
- P(Contains "win" | Not Spam) = Number of Not Spam Emails containing "win" / Total Not Spam Emails = 1 / 2 = 0.5
Step 3: Calculate Posterior Probabilities
Now, we use Bayes' Theorem to calculate the posterior probability for each class (Spam or Not Spam) given the features of the new email.
For Spam:
- P(Spam | Contains "offer", Contains "win", Does not contain "free")= P(Spam) * P(Contains "offer" | Spam) * P(Does not contain "free" | Spam) * P(Contains "win" | Spam)= 0.5 * 0.5 * (1 - 0.5) * 0.5= 0.5 * 0.5 * 0.5 * 0.5= 0.0625
For Not Spam:
- P(Not Spam | Contains "offer", Contains "win", Does not contain "free")= P(Not Spam) * P(Contains "offer" | Not Spam) * P(Does not contain "free" | Not Spam) * P(Contains "win" | Not Spam)= 0.5 * 0 * (1 - 0.5) * 0.5= 0.5 * 0 * 0.5 * 0.5= 0
Step 4: Make a Prediction
The Naive Bayes Classifier selects the class with the highest posterior probability. In this case, the probability of the email being Spam is 0.0625, while the probability of it being Not Spam is 0. Since the probability of spam is greater than the probability of not spam, the classifier predicts that the email is Spam.
Advantages of Naïve Bayes Classifier:
- Naïve Bayes is one of the fast and easy ML algorithms to predict a class of datasets.
- It can be used for Binary as well as Multi-class Classifications.
- It performs well in Multi-class predictions as compared to the other Algorithms.
- It is the most popular choice for text classification problems.
Disadvantages of Naïve Bayes Classifier:
- Naive Bayes assumes that all features are independent or unrelated, so it cannot learn the relationship between features.
Applications of Naïve Bayes Classifier:
- It is used for Credit Scoring.
- It is used in medical data classification.
- It can be used in real-time predictions because Naïve Bayes Classifier is an eager learner.
- It is used in Text classification such as Spam filtering and Sentiment analysis.
Types of Naïve Bayes Model:
There are three types of Naive Bayes Model, which are given below:
- Gaussian: The Gaussian model assumes that features follow a normal distribution. This means if predictors take continuous values instead of discrete, then the model assumes that these values are sampled from the Gaussian distribution.
- Multinomial: The Multinomial Naïve Bayes classifier is used when the data is multinomial distributed. It is primarily used for document classification problems, it means a particular document belongs to which category such as Sports, Politics, education, etc.
The classifier uses the frequency of words for the predictors. - Bernoulli: The Bernoulli classifier works similar to the Multinomial classifier, but the predictor variables are the independent Booleans variables. Such as if a particular word is present or not in a document. This model is also famous for document classification tasks.
The Optimal Bayes Classifier and the Naive Bayes Classifier are probabilistic models based on Bayes' Theorem. Still, they differ in key ways, particularly in how they handle data and make predictions. Here's a breakdown of their main differences:
1. Assumptions about Features
Optimal Bayes Classifier:
The Optimal Bayes Classifier makes no assumptions about the relationships or dependencies between the features. It considers all possible hypotheses and uses the joint distribution of the features to make predictions, which makes it theoretically the most accurate classifier if all probabilities are known.Naive Bayes Classifier:
The Naive Bayes Classifier makes a strong independence assumption: it assumes that all features are conditionally independent given the class label. This means that it simplifies the joint probability of features by treating them as independent. While this assumption is often unrealistic, it allows for faster computation and works well in many practical situations.
2. Complexity
Optimal Bayes Classifier:
The Optimal Bayes Classifier is computationally infeasible in most real-world scenarios because it requires knowledge of the full joint probability distribution of the features. Calculating this joint distribution becomes increasingly complex as the number of features grows, especially when the features are not independent.Naive Bayes Classifier:
The Naive Bayes Classifier is computationally efficient because of its independence assumption. It calculates probabilities separately for each feature and combines them to estimate the probability of a class. This makes it scalable even with large datasets and high-dimensional data.
3. Accuracy
Optimal Bayes Classifier:
The Optimal Bayes Classifier provides the most accurate possible predictions in theory, as it considers the full probability distribution of all features without making any simplifying assumptions. It minimizes the error rate and is considered the ideal classifier.Naive Bayes Classifier:
The Naive Bayes Classifier can be less accurate than the Optimal Bayes Classifier, especially when the independence assumption does not hold. However, despite its simplistic assumptions, it often performs surprisingly well in practice, particularly in cases like text classification and spam detection.
4. Training Data Requirements
Optimal Bayes Classifier:
Since it needs the full joint probability distribution of all features, the Optimal Bayes Classifier typically requires large amounts of training data to estimate these probabilities accurately.Naive Bayes Classifier:
The Naive Bayes Classifier can work with smaller datasets because it estimates probabilities for individual features independently, reducing the need for large amounts of training data.
5. Practical Use
Optimal Bayes Classifier:
It is mostly of theoretical importance and not used in practice for large, complex problems due to its computational complexity and the difficulty of obtaining complete knowledge of the joint distribution of features.Naive Bayes Classifier:
The Naive Bayes Classifier is widely used in practical applications because it is simple to implement, fast, and performs well even when its independence assumption is violated. It's commonly applied in text classification tasks, spam filtering, sentiment analysis, and medical diagnosis.
Summary of Differences
| Feature | Optimal Bayes Classifier | Naive Bayes Classifier |
|---|---|---|
| Assumptions about Features | No independence assumptions | Assumes conditional independence between features |
| Complexity | Computationally infeasible for large datasets | Computationally efficient and scalable |
| Accuracy | Theoretically optimal, minimal error rate | Less accurate if independence assumption is violated |
| Data Requirements | Requires large amounts of data to model joint probabilities | Can work with smaller datasets |
| Practical Use | Mostly theoretical, rarely used in practice | Widely used in many practical applications |
Conclusion
The Optimal Bayes Classifier is theoretically the best model, providing the most accurate predictions by considering the full joint distribution of features, but it is computationally complex and impractical for large datasets. On the other hand, the Naive Bayes Classifier simplifies the problem by assuming feature independence, making it computationally efficient and suitable for many real-world problems, even though its assumptions may not always hold.
Example: Weather Prediction
We want to predict whether it will rain or not rain based on two features:
- Cloudy: Whether the sky is cloudy.
- Windy: Whether it is windy.
Dataset
Let’s consider this simplified dataset:
| Day | Cloudy | Windy | Rain/Not Rain |
|---|---|---|---|
| 1 | Yes | Yes | Rain |
| 2 | No | Yes | Not Rain |
| 3 | Yes | No | Rain |
| 4 | Yes | Yes | Rain |
| 5 | No | No | Not Rain |
The goal is to predict whether it will rain or not rain based on whether it is cloudy and windy.
Optimal Bayes Classifier
The Optimal Bayes Classifier uses the exact joint probabilities of the features (cloudy and windy) and the class label (rain or not rain).
It calculates the posterior probabilities P(Rain | Cloudy and Windy) and P(Not Rain | Cloudy and Windy) directly by considering both features together (cloudy and windy) at the same time. This approach does not assume that cloudy and windy are independent of each other.
For example, to predict whether it will rain when it is both cloudy and windy, the Optimal Bayes Classifier would compute:
- P(Rain | Cloudy = Yes, Windy = Yes) = Number of times it was cloudy and windy and it rained / Number of times it was cloudy and windy
- P(Not Rain | Cloudy = Yes, Windy = Yes) = Number of times it was cloudy and windy and it didn’t rain / Number of times it was cloudy and windy
From the dataset:
- P(Rain | Cloudy = Yes, Windy = Yes) = 2/2 (Day 1 and Day 4 are cloudy, windy, and rainy)
- P(Not Rain | Cloudy = Yes, Windy = Yes) = 0/2 (No day is cloudy, windy, and not rainy)
So, based on this joint distribution, if it is both cloudy and windy, the Optimal Bayes Classifier would predict that it will definitely rain because all the examples with cloudy and windy conditions led to rain.
This method is very accurate but requires knowing or estimating all possible combinations of features, which can be computationally expensive and require a lot of data.
Naive Bayes Classifier
The Naive Bayes Classifier simplifies things by assuming that the features (cloudy and windy) are independent given the class label (rain or not rain). Instead of looking at the combination of cloudy and windy together, it calculates the probabilities separately and multiplies them.
In this case, the classifier calculates:
- P(Rain | Cloudy = Yes) and P(Rain | Windy = Yes)
- P(Not Rain | Cloudy = Yes) and P(Not Rain | Windy = Yes)
Then, it combines these probabilities using the assumption of independence.
Step-by-Step Calculation for Naive Bayes
Calculate Prior Probabilities:
- P(Rain) = 3/5 (Three days it rained out of five)
- P(Not Rain) = 2/5 (Two days it did not rain out of five)
Calculate Conditional Probabilities:
- P(Cloudy = Yes | Rain) = 2/3 (Two out of three rainy days were cloudy)
- P(Cloudy = Yes | Not Rain) = 0/3 (One out of two non-rainy days was cloudy)
- P(Windy = Yes | Rain) = 2/3 (Two out of three rainy days were windy)
- P(Windy = Yes | Not Rain) = 1/2 (One out of two non-rainy days was windy)
Make Prediction (if it’s both cloudy and windy):
P(Rain | Cloudy = Yes, Windy = Yes) (using independence assumption) = P(Cloudy = Yes | Rain) * P(Windy = Yes | Rain) * P(Rain)
- P(Rain | Cloudy = Yes, Windy = Yes) = (3/3) * (2/3) * (3/5) = 0.40
P(Not Rain | Cloudy = Yes, Windy = Yes) = P(Cloudy = Yes | Not Rain) * P(Windy = Yes | Not Rain) * P(Not Rain)
- P(Not Rain | Cloudy = Yes, Windy = Yes) = (0) * (1/2) * (2/5) = 0.00
Final Prediction:
- The classifier will choose the class with the higher probability. Since P(Rain | Cloudy = Yes, Windy = Yes) (0.40) is greater than P(Not Rain | Cloudy = Yes, Windy = Yes) (0.00), the Naive Bayes Classifier predicts Rain.
Key Difference in This Example:
Optimal Bayes Classifier: It directly uses the joint probability of the features together (cloudy and windy) to make a prediction. In this example, it sees that every time it was cloudy and windy, it rained, so it predicts rain with certainty.
Naive Bayes Classifier: It simplifies things by calculating probabilities for each feature separately and assumes that being cloudy and being windy are independent of each other given the class. While it also predicts rain, it does so with less certainty because it doesn't account for the possible dependency between cloudy and windy.
The Naive Bayes Classifier assumes that cloudy and windy are unrelated, which simplifies the calculation, but this assumption might not be true in reality (e.g., cloudiness and wind could be correlated). However, Naive Bayes often works surprisingly well even with this assumption.
Summary:
- The Optimal Bayes Classifier gives the most accurate result by considering the dependencies between all features but is computationally expensive and needs a lot of data.
- The Naive Bayes Classifier simplifies things by assuming that all features are independent given the class, making it faster and easier to implement, though it may be less accurate if features are highly dependent.
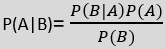




No comments:
Post a Comment