Perceptron
Perceptron was introduced by Frank Rosenblatt in 1957. He proposed a Perceptron learning rule based on the original MCP neuron. A Perceptron is an algorithm for supervised learning of binary classifiers. This algorithm enables neurons to learn and processes elements in the training set one at a time.
There are two types of Perceptrons: Single layer and Multilayer.
- Single layer - Single layer perceptrons can learn only linearly separable patterns
- Multilayer - The Multilayer Perceptron was
developed to tackle this limitation. It is a neural network where the mapping
between inputs and output is non-linear.
A Multilayer Perceptron has input and output layers, and one or more hidden layers with many neurons stacked together. And while in the Perceptron the neuron must have an activation function that imposes a threshold, like ReLU or sigmoid, neurons in a Multilayer Perceptron can use any arbitrary activation function.
Multilayer Perceptron falls under the
category of feedforward algorithms, because inputs are combined with the
initial weights in a weighted sum and subjected to the activation function,
just like in the Perceptron. But the difference is that each linear combination
is propagated to the next layer.
Each layer is feeding the
next one with the result of their computation, their internal representation of
the data. This goes all the way through the hidden layers to the output layer.
If the algorithm only computed the weighted
sums in each neuron, propagated results to the output layer, and stopped there,
it wouldn’t be able to learn the weights that minimize the
cost function. If the algorithm only computed one iteration, there would be no
actual learning.
This enables you to distinguish between the two linearly separable classes +1 and -1.
Note: Supervised Learning is a type of Machine Learning used to learn models from labeled training data. It enables output prediction for future or unseen data. Let us focus on the Perceptron Learning Rule in the next section.
Perceptron Learning Rule
Perceptron Learning Rule states that the algorithm would automatically learn the optimal weight coefficients. The input features are then multiplied with these weights to determine if a neuron fires or not.
The Perceptron receives multiple input signals, and if the sum of the input signals exceeds a certain threshold, it either outputs a signal or does not return an output. In the context of supervised learning and classification, this can then be used to predict the class of a sample.
Perceptron Function
Perceptron is a function that maps its input “x,” which is multiplied with the learned weight coefficient; an output value ”f(x)”is generated.
In the equation given above:
- “w” = vector of real-valued weights
- “b” = bias (an element that adjusts the boundary away from origin without any dependence on the input value)
- “x” = vector of input x values
- “m” = number of inputs to the Perceptron
The output can be represented as “1” or “0.” It can also be represented as “1” or “-1” depending on which activation function is used.
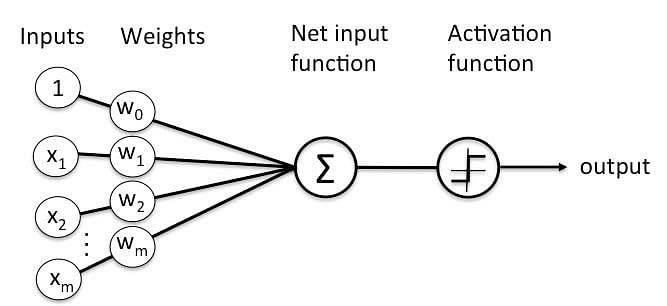
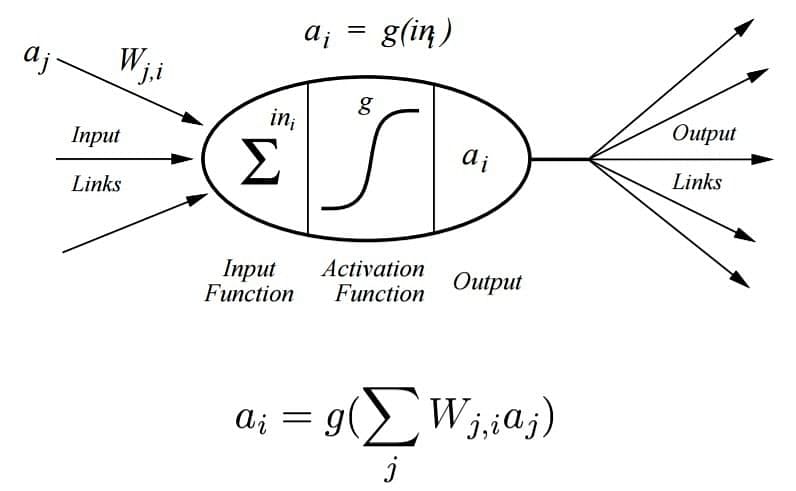
Inputs of a Perceptron
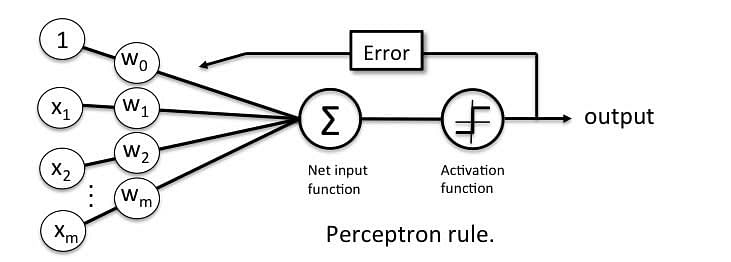
A Perceptron accepts inputs, moderates them with certain weight values, then applies the transformation function to output the final result. The image below shows a Perceptron with a Boolean output.
A Boolean output is based on inputs such as salaried, married, age, past credit profile, etc. It has only two values: Yes and No or True and False. The summation function “∑” multiplies all inputs of “x” by weights “w” and then adds them up as follows:
Activation Functions of Perceptron
The activation function applies a step rule (convert the numerical output into +1 or -1) to check if the output of the weighting function is greater than zero or not.
For example:
If ∑ wixi> 0 => then final output “o” = 1 (issue bank loan)
Else, final output “o” = -1 (deny bank loan)
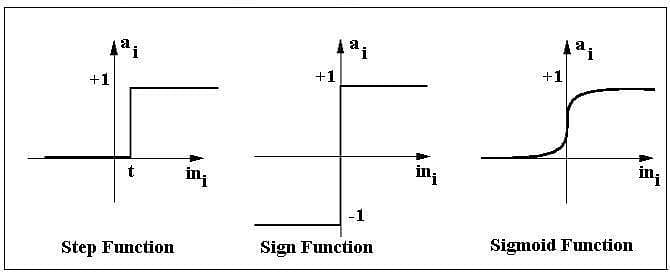
Step function gets triggered above a certain value of the neuron output; else it outputs zero. Sign Function outputs +1 or -1 depending on whether neuron output is greater than zero or not. Sigmoid is the S-curve and outputs a value between 0 and 1.
Output of Perceptron
Perceptron with a Boolean output:
Inputs: x1…xn
Output: o(x1….xn)
Weights: wi=> contribution of input xi to the Perceptron output;
w0=> bias or threshold
If ∑w.x > 0, output is +1, else -1. The neuron gets triggered only when weighted input reaches a certain threshold value.
An output of +1 specifies that the neuron is triggered. An output of -1 specifies that the neuron did not get triggered.
“sgn” stands for sign function with output +1 or -1.
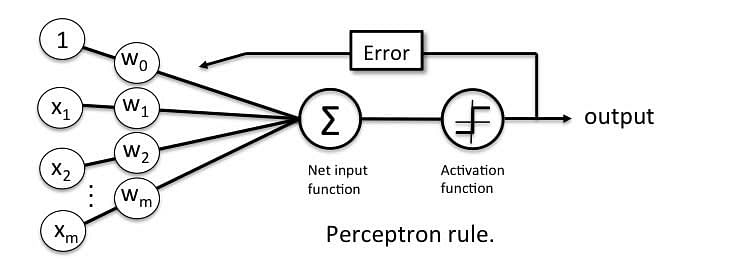
Error in Perceptron
In the Perceptron Learning Rule, the predicted output is compared with the known output. If it does not match, the error is propagated backward to allow weight adjustment to happen.
Perceptron: Decision Function
A decision function φ(z) of Perceptron is defined to take a linear combination of x and w vectors.
The value z in the decision function is given by:
The decision function is +1 if z is greater than a threshold θ, and it is -1 otherwise.
This is the Perceptron algorithm.
Bias Unit
For simplicity, the threshold θ can be brought to the left and represented as w0x0, where w0= -θ and x0= 1.
The value w0 is called the bias unit.
The decision function then becomes:
Output:
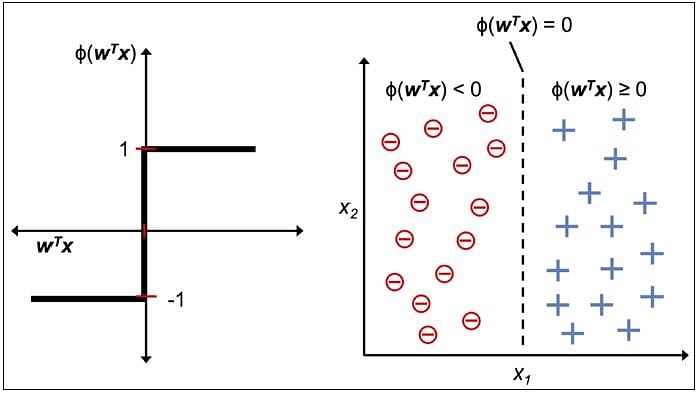
The figure shows how the decision function squashes wTx to either +1 or -1 and how it can be used to discriminate between two linearly separable classes.
Perceptron at a Glance
Perceptron has the following characteristics:
- Perceptron is an algorithm for Supervised Learning of single layer binary linear classifiers.
- Optimal weight coefficients are automatically learned.
- Weights are multiplied with the input features and decision is made if the neuron is fired or not.
- Activation function applies a step rule to check if the output of the weighting function is greater than zero.
- Linear decision boundary is drawn enabling the distinction between the two linearly separable classes +1 and -1.
- If the sum of the input signals exceeds a certain threshold, it outputs a signal; otherwise, there is no output.
Types of activation functions include the sign, step, and sigmoid functions.
Implement Logic Gates with Perceptron
Perceptron - Classifier Hyperplane
The Perceptron learning rule converges if the two classes can be separated by the linear hyperplane. However, if the classes cannot be separated perfectly by a linear classifier, it could give rise to errors.
As discussed in the previous topic, the classifier boundary for a binary output in a Perceptron is represented by the equation given below:
The diagram above shows the decision surface represented by a two-input Perceptron.
Observation:
- In Fig(a) above, examples can be clearly separated into positive and negative values; hence, they are linearly separable. This can include logic gates like AND, OR, NOR, NAND.
- Fig (b) shows examples that are not linearly separable (as in an XOR gate).
- Diagram (a) is a set of training examples and the decision surface of a Perceptron that classifies them correctly.
- Diagram (b) is a set of training examples that are not linearly separable, that is, they cannot be correctly classified by any straight line.
- X1 and X2 are the Perceptron inputs.
Sigmoid Activation Function
The diagram below shows a Perceptron with sigmoid activation function. Sigmoid is one of the most popular activation functions.
A Sigmoid Function is a mathematical function with a Sigmoid Curve (“S” Curve). It is a special case of the logistic function and is defined by the function given below:
Here, value of z is:
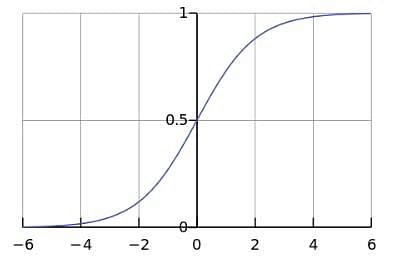
Sigmoid Curve
The curve of the Sigmoid function called “S Curve” is shown here.
This is called a logistic sigmoid and leads to a probability of the value between 0 and 1.
This is useful as an activation function when one is interested in probability mapping rather than precise values of input parameter t.
The sigmoid output is close to zero for highly negative input. This can be a problem in neural network training and can lead to slow learning and the model getting trapped in local minima during training. Hence, hyperbolic tangent is more preferable as an activation function in hidden layers of a neural network.
Ques. Explain a multilayer perceptron with its architecture and characteristics.
Answer
- An MLP consists of at least three layers of nodes: an input layer, a hidden layer and an output layer.
- Except for the input nodes, each node is a neuron that uses a nonlinear activation function.
- MLP utilizes a supervised learning technique called backpropagation for training.
- Its multiple layers and non-linear activation distinguish MLP from a linear perceptron.
- It can distinguish data that is not linearly separable.
- Since MLPs are fully connected, each node in one layer connects with a certain weight W ij to every node in the following layer.
- The development of MLP networks has two main problems: architecture optimization and training.
- Different approaches have been proposed to optimize the architecture of an MLP network, for example, back-propagation, genetic algorithms,etc.
- Each layer can have a large number of perceptrons, and there can be multiple layers, so the multilayer perceptron can quickly become a very complex system.
- It has one or more hidden layers between its input and output layers, the neurons are organized in layers, the connections are always directed from lower layers to upper layers, the neurons in the same layer are not interconnected
Ques. How tuning parameters affect the backpropagation neural network?
Answer:
Parameters are updated so that they can converge towards the minimum of the loss function
Effect of tuning parameters of the backpropagation neural network:
- Momentum factor: It basically increases the speed of convergence not in terms of learning rate
- Learning Coefficient
- Sigmoidal Gain
- Threshold value:They are used to compare the output value.
Ques. Discuss selection of various parameters Backpropagation Neural Network (BPN).
Answer
Various Parameters of Backpropagation Neural Network (BPN) are listed below:
- Hidden Nodes:The Hidden layer of the neural network is the intermediate layer between Input and Output layer.Each node in the input and hidden layers is connected to each of the nodes in the next layer
- Momentum coefficient:
- Sigmoidal Gain:
- Local Minima:

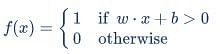
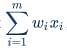
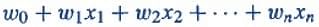
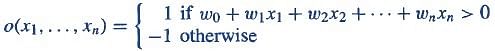
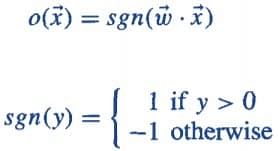
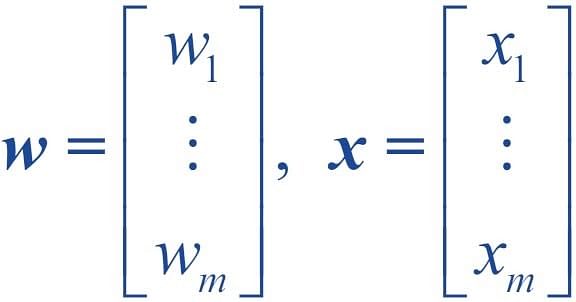

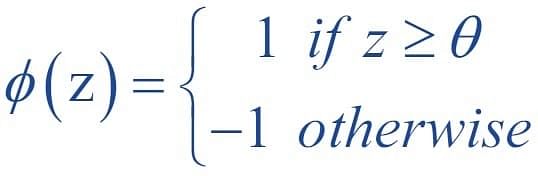
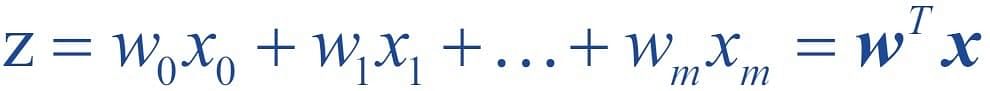
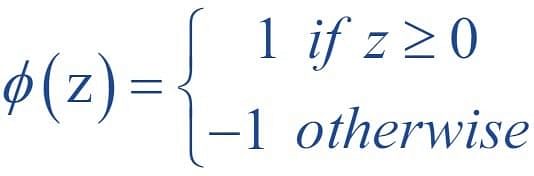
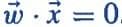
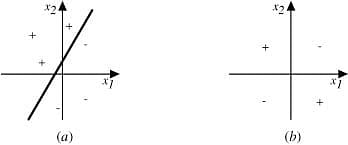
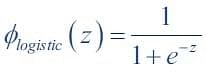
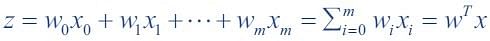




No comments:
Post a Comment