Eliminating ε Transitions

Epsilon NFA  (∈-NFA)

Epsilon NFA (∈-NFA) is similar to the NFA but have just a minor difference which is epsilon (∈) move. The transitions without consuming an input symbol are called ∈-transitions.

• In the state diagrams, they are usually labeled with the Greek letter ∈ also called lamda.
• ∈-transitions provide a convenient way of modeling the systems
• Due to empty move, the first string of language may be a empty or epsilon.

Note: ∈ab∈a = aba, where ∈ is empty.

Formal Definition of Epsilon-NFA

The formal definition of  ∈-NFA is represented through 5-tuple (Q, ∑, δ, q0, F) where,

• Q is a finite set of all states (q0, q1, q2,   … qn) where n is finite number
• ∑ is a finite set of symbols called the alphabet. i.e. {0, 1},
• δ : Q x (∑ U ∈) → 2Q is a total function called as transition function
• q0 is the initial state from where any input is processed (q0 ∈ Q).
• F is a set of final state/states where F will be subset ( ⊆ ) of Q.

Eliminating ε Transitions

NFA with ε can be converted to NFA without ε, and this NFA without ε can be converted to DFA. To do this, we will use a method, which can remove all the ε transition from given NFA. The method will be:

1. Find out all the ε transitions from each state from Q. That will be called as ε-closure{q1} where qi ∈ Q.
2. Then δ' transitions can be obtained. The δ' transitions mean a ε-closure on δ moves.
3. Repeat Step-2 for each input symbol and each state of given NFA.
4. Using the resultant states, the transition table for equivalent NFA without ε can be built.

Example:

Convert the following NFA with ε to NFA without ε.

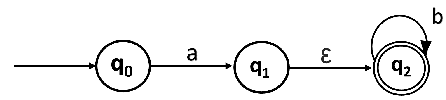
Solutions: We will first obtain ε-closures of q0, q1 and q2 as follows:

ε-closure(q0) = {q0}  

ε-closure(q1) = {q1, q2}  

ε-closure(q2) = {q2}   

Now the δ' transition on each input symbol is obtained as:

δ'(q0, a) = ε-closure(δ(δ^(q0, ε),a))  

              = ε-closure(δ(ε-closure(q0),a))  

              = ε-closure(δ(q0, a))  

             = ε-closure(q1)  

              = {q1, q2}  

(q0, b) = ε-closure(δ(δ^(q0, ε),b))  

              = ε-closure(δ(ε-closure(q0),b))  

             = ε-closure(δ(q0, b))  

              = Ф  

 Now the δ' transition on q1 is obtained as:

δ'(q1, a) = ε-closure(δ(δ^(q1, ε),a))  

              = ε-closure(δ(ε-closure(q1),a))  

              = ε-closure(δ(q1, q2), a)  

              = ε-closure(δ(q1, a) ∪ δ(q2, a))  

              = ε-closure(Ф ∪ Ф)  

              = Ф  

δ'(q1, b) = ε-closure(δ(δ^(q1, ε),b))  

              = ε-closure(δ(ε-closure(q1),b))  

              = ε-closure(δ(q1, q2), b)  

              = ε-closure(δ(q1, b) ∪ δ(q2, b))  

              = ε-closure(Ф ∪ q2)  

              = {q2}  

 

The δ' transition on q2 is obtained as:

δ'(q2, a) = ε-closure(δ(δ^(q2, ε),a))  

              = ε-closure(δ(ε-closure(q2),a))  

              = ε-closure(δ(q2, a))  

              = ε-closure(Ф)  

              = Ф  

δ'(q2, b) = ε-closure(δ(δ^(q2, ε),b))  

              = ε-closure(δ(ε-closure(q2),b))  

              = ε-closure(δ(q2, b))  

              = ε-closure(q2)  

              = {q2}  

 

Now we will summarize all the computed δ' transitions:

δ'(q0, a) = {q0, q1}  

δ'(q0, b) = Ф  

δ'(q1, a) = Ф  

δ'(q1, b) = {q2}  

δ'(q2, a) = Ф  

δ'(q2, b) = {q2}  

 

The transition table can be:

States	a	b
→q0	{q1, q2}	Ф
*q1	Ф	{q2}
*q2	Ф	{q2}

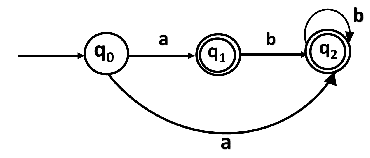
State q1 and q2 become the final state as ε-closure of q1 and q2 contain the final state q2. The NFA can be shown by the following transition diagram: