Examples of NFA

Example 1:

Design a NFA for the transition table as given below:

Present State	0	1
→q0	q0, q1	q0, q2
q1	q3	ε
q2	q2, q3	q3
→q3	q3	q3

The transition diagram can be drawn by using the mapping function as given in the table.Solution:

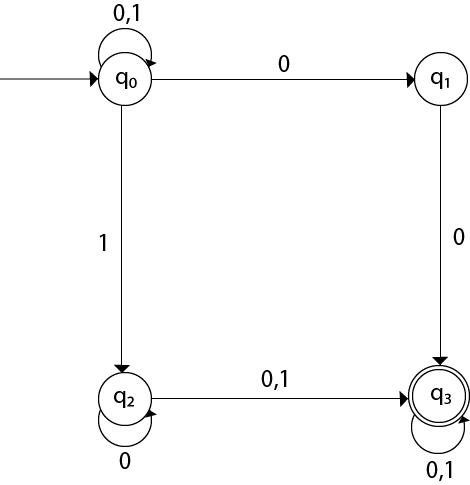
Here,

 δ(q0, 0) = {q0, q1}  

      δ(q0, 1) = {q0, q2}  

Then, δ(q1, 0) = {q3}  

Then, δ(q2, 0) = {q2, q3}  

      δ(q2, 1) = {q3}  

Then, δ(q3, 0) = {q3}  

      δ(q3, 1) = {q3}       

Example 2:

Design an NFA with ∑ = {0, 1} accepts all string ending with 01.

Solution:

Hence, NFA would be:

Example 3:

Design an NFA with ∑ = {0, 1} in which double '1' is followed by double '0'.

Solution:

The FA with double 1 is as follows:

It should be immediately followed by double 0.

Then,

Now before double 1, there can be any string of 0 and 1. Similarly, after double 0, there can be any string of 0 and 1.

Hence the NFA becomes:

Now considering the string 01100011

q0 → q1 → q2  → q3 → q4 → q4 → q4 → q4  

Example 4:

Design an NFA in which all the string contain a substring 1110.

Solution:

The language consists of all the string containing substring 1010. The partial transition diagram can be:

Now as 1010 could be the substring. Hence we will add the inputs 0's and 1's so that the substring 1010 of the language can be maintained. Hence the NFA becomes:

Transition table for the above transition diagram can be given below:

Present State	0	1
→q1	q1	q1, q2
q2		q3
q3		q4
q4	q5
*q5	q5	q5

δ(q1, 111010) = δ(q1, 1100)  Consider a string 111010,

                    = δ(q1, 100)  

                    = δ(q2, 00)  

Got stuck! As there is no path from q2 for input symbol 0. We can process string 111010 in another way.

δ(q1, 111010) = δ(q2, 1100)  

                    = δ(q3, 100)  

                    = δ(q4, 00)  

                    = δ(q5, 0)  

                    = δ(q5, ε)   

As state q5 is the accept state. We get the complete scanned, and we reached to the final state.

Example 5:

Design an NFA with ∑ = {0, 1} accepts all string in which the third symbol from the right end is always 0.

Solution:

Thus we get the third symbol from the right end as '0' always. The NFA can be:

The above image is an NFA because in state q0 with input 0, we can either go to state q0 or q1.

Example of Non-Deterministic Finite Automata Without Epsilon-

 

Following automata is an example of Non-Deterministic Finite Automata without epsilon-

 

 

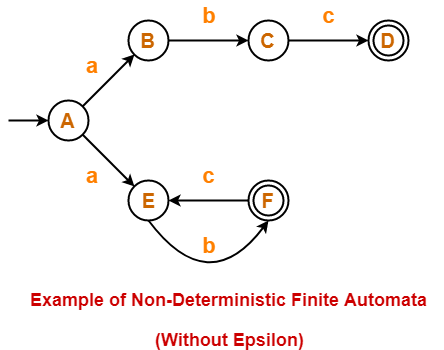
The above NFA can be defined in form of five tuples as-

{ {A, B, C, D, E, F}, {a, b, c}, δ, A, {D, F} }

 

where-

• {A, B, C, D, E, F} refers to the set of states
• {a, b, c} refers to the set of input alphabets
• δ refers to the transition function
• A refers to the the initial state
• {D, F} refers to the set of final states

 

Transition function δ is defined as-

• δ (A, a) = B
• δ (A, a) = E
• δ (B, b) = C
• δ (C, c) = D
• δ (E, b) = F
• δ (F, c) = E

 

Transition Table for the above Non-Deterministic Finite Automata is-

 

States / Alphabets	a	b	c
A	{B, F}	–	–
B	–	C	–
C	–	–	D
D	–	–	–
E	–	F	–
F	–	–	E

 

Example of Non-Deterministic Finite Automata With Epsilon-

 

Following automata is an example of Non-Deterministic Finite Automata with epsilon-

 

 

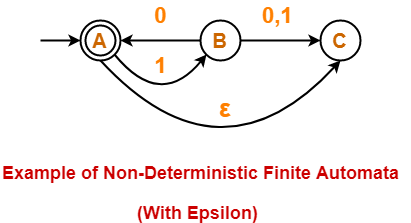
The above NFA can be defined in form of five tuples as-

{ {A, B, C}, {0, 1}, δ, A, {A} }

 

where-

• {A, B, C} refers to the set of states
• {0, 1} refers to the set of input alphabets
• δ refers to the transition function
• A refers to the the initial state
• {A} refers to the set of final states

 

Transition function δ is defined as-

• δ (A, 1) = B
• δ (A, ∈) = C
• δ (B, 0) = A
• δ (B, 0) = C
• δ (B, 1) = C

 

Transition Table for the above Non-Deterministic Finite Automata is-

 

States / Alphabets	0	1	∈
A	–	B	C
B	{A, C}	C	–
C	–	–	–

 

Dead Configuration or Trap State-

 

In Non-Deterministic Finite Automata,

• The result of a transition function may be empty.
• In such a case, automata gets stopped forcefully after entering that configuration.
• This type of configuration is known as dead configuration.
• The string gets rejected after entering the dead configuration.

 

Equivalence of DFA and NFA-

 

Two finite accepters are said to be equal in power if they both accepts the same language. DFA and NFA are both exactly equal in power.

 

Example-

 

Consider a language L(M) = { (10)ⁿ : n >= 0 }

 

Equivalent NFA for the language L(M) is-

 

 

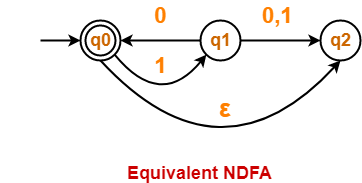
Equivalent DFA for the language L(M) is-

 

 

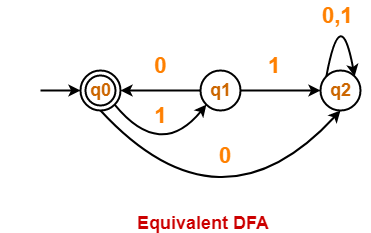
• Both the above automata accepts the same language L(M).
• Thus, both are equal in power.

 

Important Points   It is important to note the following points- Both DFA and NFA are exactly same in power. For any regular language, both DFA and NFA can be constructed. There exists an equivalent DFA corresponding to every NFA. Every NFA can be converted into its equivalent DFA. There exists no NFA that can not be converted into its equivalent DFA. Every DFA is a NFA but every NFA is not a DFA.

 

Acceptance by NFA-

 

A string ‘w’ is said to be accepted by a NFA if there exists at least one transition path on which we start at initial state and ends at final state. δ* (q0, w) = F

 

Example-

 

Consider the following NFA-

 

For the string w = ab,

• There exists two transition paths.
• One transition path starts at initial state and ends at final state.
• Therefore, string w = ab is accepted by the NFA.